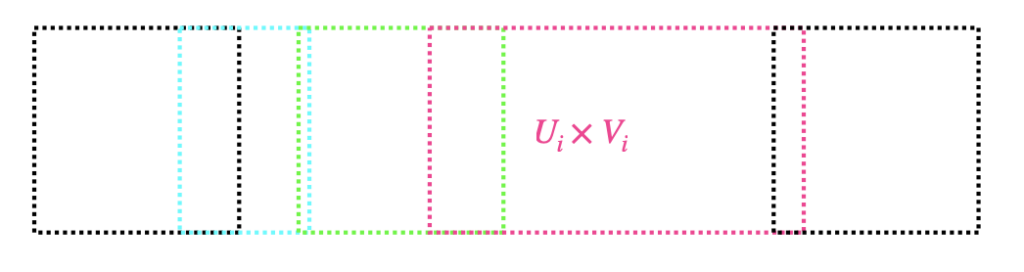Last time I mentioned that S0 is not consonant. I had a preprint by Matthew de Brecht where he proved that, but I could not find the result in published form. Since then, M. de Brecht wrote to me, and told me a lot of interesting things. First, his proof can be found in [1]. His proof uses a topological game first invented by Till Plewe [2] in order to study locale products of spaces, and conditions under which the locale products coincide with the (locales underlying) the topological products, which M. de Brecht had initially used to show that the locale product of S0 with itself is not spatial. Second, he pointed me towards an intriguing result by Ruiyuan Chen [3], which gives another connection between locale products (of dcpos) and the question of whether the poset-theoretic product of two dcpos with the Scott topology coincides with the topological product. Third, R. Chen has a simpler, alternative proof of the fact that the locale product of S0 with itself is not spatial [4]. And so on!
Hence I have too much to talk about, so I will have to make a choice. I will concentrate on explaining what [1] is all about. I am afraid that this post will mostly be paraphrasing M. de Brecht’s paper. I have merely added a few pictures, and I have reformulated a few notions; I hope this will contribute to make what he achieved easier to grasp.
Till Plewe’s game
Let X and Y be two topological spaces, U0 be an open subset of X, V0 be an open subset of Y, and U be an open cover of U0 × V0 by open rectangles. Till Plewe’s game GX,Y(U0, V0, U) is played as follows. At each turn i≥1:
- player I picks a point xi ∈ Ui–1;
- then player II picks an open neighborhood Ui of xi included in Ui–1;
- player I picks a point yi ∈ Vi–1;
- then player II picks an open neighborhood Vi of yi included in Vi–1.
So, yes, each player plays twice at each turn.
Player II wins (at round i) if Ui × Vi is included in one of the open rectangles of the cover U. Otherwise, namely if the play goes along without player II even winning, player I wins.
The following in Theorem 1.1 in [2].
Theorem (Plewe). If X and Y are sober spaces, either:
- for every open subset U0 of X, for every open subset V0 of Y, for every open cover U of U0 × V0 by open rectangles, player II has a winning strategy in the game GX,Y(U0, V0, U), and then the locale product of X and of Y is spatial;
- or there is an open subset U0 of X, there is an open subset V0 of Y, and there is an open cover U of U0 × V0 by open rectangles such that player I has a winning strategy in the game GX,Y(U0, V0, U), and then the locale product of X and of Y is non-spatial.
And the following is Theorem 4 in [1].
Theorem (de Brecht). If X is a consonant space, then for every open cover U of X × X by open rectangles, player II has a winning strategy in the game GX,X(X, X, U).
Hence there is an intriguing connection between consonance and the spatiality of products of locales, which seems to me to be largely unexplored. M. de Brecht says “However, the implicit connections we make in this paper are not as strong as we expect they really are” at the end of the introduction of [1]. I don’t quite know what he means by that, except perhaps that he finds them intriguing, and unexplored, too.
I will not prove Plewe’s theorem here, but I will definitely give de Brecht’s proof of his theorem, and I will then explain how he uses it to prove that S0 is not consonant. He also hints at the fact that this can be used to show that Q is not consonant. We have suffered quite a lot through the latter question, and I should take a stab at it some day, and explain what M. de Brecht had in mind in this respect—but not today.
An ordinal measure of open rectangles
The key to proving the above theorem by M. de Brecht is to realize that given any open cover U of X × X by open rectangles, where X is consonant, one can eventually reach the open rectangle X × X itself by repeating the operations of horizontal unions and vertical unions, transfinitely often, starting from the downward closure of U. Let me explain.
The terms horizontal unions and vertical unions will be specific to this post. If you are given a collection A of open rectangles, then I will call a horizontal union of elements of A any union ∪i ∈ I (Ui × Vi), where each Ui × Vi is in A, and all the open sets Vi are identical. In other words, this is obtained by putting side by side, horizontally, any number of open rectangles from A with the same vertical cross-section. Vertical unions are defined similarly; namely, in that case, we require all the open sets Ui to be identical instead.
The downward closure ↓U of an open cover U is by definition the collection of open rectangles that are included in some element of U. We define A0(U) as ↓U. For every ordinal α, if we have already defined Aα(U), we define Aα+1(U) as the collection of horizontal unions of elements of Aα(U), plus all vertical unions of elements of Aα(U). (In particular, Aα(U) is included in Aα+1(U), since one can reobtain any rectangle of Aα(U) as, say, a horizontal union of just one rectangle from Aα(U).) For a limit ordinal α, Aα(U) is the union of the collections Aβ(U), β<α.
Lemma. For every ordinal α, Aα(U) is downward closed.
Proof. By induction on α. Since A0(U) = ↓U, A0(U) is downward closed. Assuming Aα(U) downward closed, we show that Aα+1(U) is downward closed by showing that any open rectangle U × V included in some horizontal union ∪i ∈ I (Ui × Vi) of rectangles in Aα(U) is already in Aα+1(U) (and similarly for vertical unions; but the argument is symmetrical, hence omitted). This is easy: U × V is equal to ∪i ∈ I ((Ui ∩ U) × (Vi ∩ V)), which is a horizontal union of rectangles (Ui ∩ U) × (Vi ∩ V); each such rectangle is a subset of a rectangle in Aα(U), hence is in Aα(U) by induction hypothesis, so U × V = ∪i ∈ I ((Ui ∩ U) × (Vi ∩ V)) is also a horizontal union of elements of Aα(U); therefore U × V is in Aα+1(U). ☐
Let us write A∞(U) for the union of the monotone sequence of collections Aα(U). A∞(U) must be obtained as Aα(U) for some large enough ordinal α, since otherwise A∞(U) would contain at least as many elements as there are ordinals, namely: A∞(U) would be a proper class. And A∞(U) cannot be a proper class, since it is included in a set—namely the set of all open rectangles on X × X.
It follows that A∞(U) is closed under both horizontal and vertical unions.
Lemma. A∞(U) is Scott-closed in OX × OX.
Proof. Let (Ui × Vi)i ∈ I be a directed family of elements of A∞(U), and let U × V be its union. Without loss of generality, we may assume that none of the rectangles Ui × Vi is empty; otherwise, remove all of them and what remains will either be an empty family (and the union of the empty family is in A1(U), hence in A∞(U)) or will still be directed. Therefore every Ui, and every Vi, will now be considered as non-empty.
The first thing we need to observe is that every rectangle Uj × Vi, where i and j are possibly distinct indices in I, is in A∞(U). Indeed, since the family is directed, we can find an index k in I such that both Ui × Vi and Uj × Vj are included in Uk × Vk. In particular, and because neither Uj nor Vi is empty, Uj is included in Uk and Vi is included in Vk. But Uk × Vk is in A∞(U), and A∞(U) is downwards closed, so Uj × Vi is in A∞(U), too.
Fixing i ∈ I, U × Vi is the union of the sets Uj × Vi, where j ranges over I. That is a horizontal union of elements of A∞(U), hence is itself in A∞(U). Then U × V is the union of the sets U × Vi, where i ranges over I, hence is a vertical union of elements of A∞(U). It follows that U × V is also in A∞(U). ☐
Let us define C(U) as the collection of open subsets U of X such that U × U is in A∞(U). The map U ↦ U × U is Scott-continuous from OX to OX × OX, so C(U) is Scott-closed in OX.
Let H(U) be the complement of C(U) in OX, namely the collection of open subsets U of X such that U × U is not in A∞(U). We have just proved:
Fact. H(U) is a Scott-open subset of OX.
This is where consonance comes into play. Let me recall (from any of the earlier posts on the topic, namely 1 through 5 on this page) that a space X is consonant if and only if every Scott-open subset of OX is a union of sets of the form ■Q, where Q is compact saturated in X; and ■Q is the collection of open neighborhoods of Q.
Lemma. If X is consonant, then X does not belong to H(U); equivalently, X × X is in A∞(U).
Proof. If X ∈ H(U) and X is consonant, then there is a compact saturated subset Q of X such that (X is in ■Q, which is obvious, and) ■Q is included in H(U). We aim for a contradiction.
We recall that U is an open cover of X × X by open rectangles. In particular, for every point x in X, {x} × Q is included in the union of the open rectangles of U. Since {x} × Q is compact, it is included in a finite union ∪y ∈ E(x) (Uxy × Vxy) of open rectangles of U; notably, the index set E(x) is finite. Let Ux be the intersection ∩y ∈ E(x) Uxy, and let Vx be the union ∪y ∈ E(x) Vxy. We obtain that {x} × Q is included in Ux × Vx. Note in particular that Q is included in Vx.
Additionally, Ux × Vx is the vertical union of the rectangles Ux × Vxy, y ∈ E(x). Since each Ux × Vxy is included in Uxy × Vxy, which is in U, Ux × Vxy is in A0(U) = ↓U. Therefore Ux × Vx is in A1(U).
We use the compactness of Q once again: Q is included in a finite union U ≝ ∪x ∈ E Ux (namely, the index set E is finite). Let V be the intersection ∩x ∈ E Vx. Since each Vx contains Q, V also contains Q. Then U × V is a horizontal union of open rectangles Ux × V. Each of these open rectangles is included in Ux × Vx, hence is in A1(U). It follows that U × V is in A2(U).
Then open rectangle (U ∩ V) × (U ∩ V) is included in the latter, hence is also in A2(U). Additionally, both U and V contain Q, so U ∩ V is in ■Q. Since ■Q is included in H(U), U ∩ V is in H(U), or equivalently, (U ∩ V) × (U ∩ V) is not in A∞(U). This directly contradicts the fact that it is in A2(U). ☐
For every open rectangle U × V in A∞(U), there is least ordinal α such that U × V is in Aα(U). Let us call α the degree of the rectangle U × V.
It is clear that the degree of each rectangle in A∞(U) is a successor ordinal β+1. We have just proved that if X is consonant, then the degree of X × X is a well-defined notion.
Winning Plewe’s game on consonant spaces
Let me recall that M. de Brecht’s theorem states that if X is a consonant space, then for every open cover U of X × X by open rectangles, player II has a winning strategy in the game GX,X(X, X, U). We start with the open rectangle X × X, which has a well-defined degree, as we have just seen. Player II’s strategy will consist in finding open sets Ui and Vi, at round i, for each i≥1, in response to player I’s choice of points xi and yi, in such a way that the degree of Ui × Vi is strictly smaller than that of Ui–1 × Vi–1, unless the degree of Ui–1 × Vi–1 is already equal to 0. If the latter happens, then Ui–1 × Vi–1 is in A0(U) = ↓U, in which case player II has won.
Hence, let us assume that we enter round i with an open rectangle Ui–1 × Vi–1 of degree β+1. (We remember that the degree is always a successor ordinal.) Hence Ui–1 × Vi–1 is either a horizontal or vertical union of rectangles of degrees at most β.
- If Ui–1 × Vi–1 is a horizontal union of rectangles U’j × Vi–1 (j ∈ J) of degrees at most β, we reason as follows. Player I plays a point xi in Ui–1. Then xi belongs to some U’j, and we let player II play U’j for the next open set Ui. Player I then plays a point yi in Vi–1, and we let player II play Vi–1 itself for Vi (no change). As promised, the degree of Ui × Vi is at most β, hence strictly below the degree β+1 of Ui–1 × Vi–1.
- If Ui–1 × Vi–1 is a vertical union of rectangles Ui–1 × V’j (j ∈ J) of degrees at most β, then player I plays xi in Ui–1, and this time player II simply plays Ui–1 for Ui (no change). Player I plays yi in Vi–1. Then yi is in some V’j, and player II plays that V’j for Vi. Once again, the degree of Ui × Vi is at most β, hence strictly below the degree β+1 of Ui–1 × Vi–1.
Since the degree of Ui × Vi decreases strictly at each round, and the ordering on ordinals is well-founded, eventually that degree must reach 0. As we have seen above, in that situation, player II has won the game.
Hence we have proved de Brecht’s theorem, which we repeat here:
Theorem (de Brecht). If X is a consonant space, then for every open cover U of X × X by open rectangles, player II has a winning strategy in the game GX,X(X, X, U).
S0 is not consonant I: the setup
M. de Brecht uses this to show that S0 is not consonant [1, Section 4]. We use the contrapositive of the previous theorem: it suffices to show that player II does not have a winning strategy in the game GX,X(X, X, U), for some open cover U of X × X (with X ≝ S0). In order to do so, we show that player I has a winning strategy in this game.
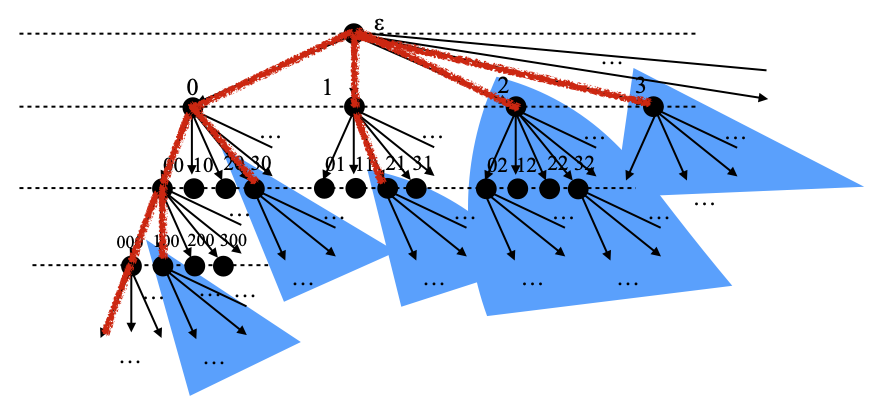
Let me recap a few things about S0 from last time. S0 is the space of finite sequences of natural numbers, with the upper topology of the (opposite of the) suffix ordering. I write n::s for the list obtained from the list s by adding a number n in front, ε for the empty list, and then S0 is a tree with the root ε at the top:
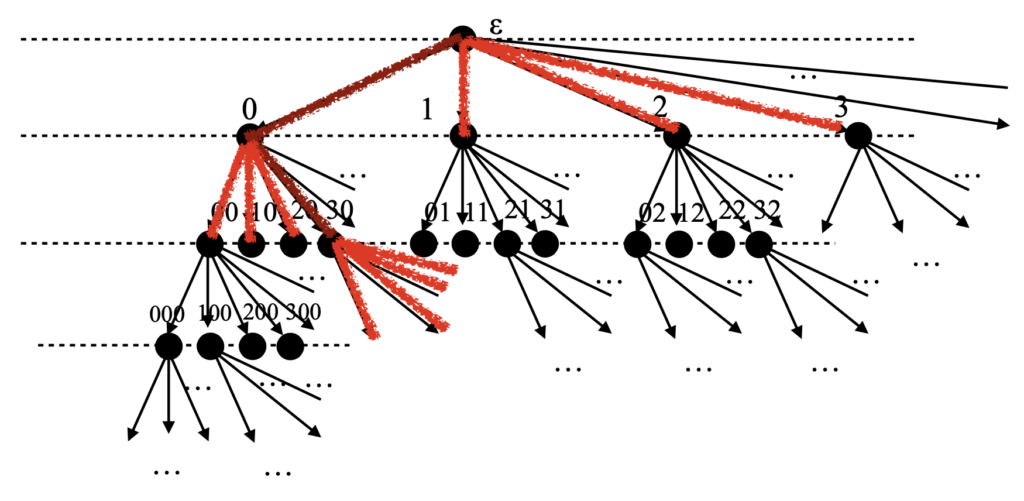
Let me also recall that the closed subsets of S0 (hence also the open subsets of S0) are in one-to-one correspondence with the finitely branching subtrees of S0. In other words, a closed subset C is the same thing as the downward closure ↓Min T of the set Min T of leaves of a finitely branching subtree T of S0. In the following picture, the tree is shown in red, and the closed set in blue. A subtree is simply an upwards-closed subset of S0; in particular, mind that we accept the empty set as a subtree.
Since the open sets are the complements of the closed sets, the open sets are also characterized through finitely branching subtrees T, namely as the sets S0–↓Min T of points that are not below any leaf of T.
M. de Brecht defines specific open subsets Uσ,τ, where σ and τ are finite lists of natural numbers, but I will make two modifications to this presentation. First, τ is not really used in the definition except for its length, so I will replace it with a natural number n, and I will write the corresponding open sets as Uσ,n. Second, it is easier to understand what these open sets are through the trees Tσ,n that are used to define them.
Tσ,n is defined as consisting of ε, plus the sequences k::s, where 0≤k≤|σ|+n and s ranges over the suffixes of σ. (|σ| denotes the length of σ.) In other words, draw the path from the root ε to σ, and add the first |σ|+n+1 successors of each node thus obtained. Here is what Tσ,n is for σ = 2::0::ε and n=1. The path σ itself is shown in brown, and the additional successors are obtained by following the additional red edges.
The leaves of Tσ,n are exactly the sequences k::s of natural numbers such that:
- s is a suffix of σ (i.e., above σ);
- 0≤k≤|σ|+n;
- and k::s is not a suffix of σ (otherwise it would be an internal vertex of Tσ,n).
The open set Uσ,n is the open set defined by Tσ,n, namely the set S0–↓Min Tσ,n of vertices that are below no leaf of Tσ,n.
I originally thought it might be easier to reason on finitely branching subtrees directly, instead of on open subsets of S0, but that would get us lost. Instead, I will be following M. de Brecht; we make the following observations, which will distill the properties on finitely branching subtrees that we need in the proof to come, in terms of open sets:
- Property (A). For every finite sequence σ of natural numbers, for every natural number n, for every element s of Uσ,n, in order to show that s is above σ, it suffices to show that every element of s (seen as a finite sequence of natural numbers) is ≤|σ|+n.
- Property (B). For every open subset U of S0, for every σ ∈ U, there are infinitely many successors n::σ of σ such that the complete subtree ↓(n::σ) is included in U.
Those are proved as follows. For property (B), we write U as the set of points that are not below any leaf of some given finitely branching tree T. Hence σ is not below any leaf of T. Since T is finitely branching, there are infinitely many natural numbers such that n::σ is not in T. Let us consider any such n, and any element t of ↓(n::σ). If t were below some leaf x of T, then x would either have n::σ as a suffix or be itself a suffix of σ. The first case would imply that n::σ is in T, since T is upwards closed, and that is impossible, by definition of n. The second case would imply that σ would be below some leaf of T, which is impossible as well. Therefore t is in U.
For property (A), let us imagine that s is the list m1::…::mp::ε, and that each mi is ≤|σ|+n. Since s is in Uσ,n, s does not have a suffix that would be a leaf of Tσ,n. For every i with 1≤i≤p, let us consider the suffix mi::…::mp::ε of s. That is not a leaf of Tσ,n, as we have just said: hence mi+1::…::mp::ε is not a suffix of σ, or mi>|σ|+n, or mi::…::mp::ε is a suffix of σ, by definition of the leaves of Tσ,n. The middle alternative mi>|σ|+n is impossible by assumption, so mi+1::…::mp::ε is not a suffix of σ or mi::…::mp::ε is a suffix of σ. In other words, exploiting that “not a or b” is the same as “if a then b”, if mi+1::…::mp::ε is a suffix of σ then mi::…::mp::ε is a suffix of σ. We use this to show that mi::…::mp::ε is a suffix of σ for every i with 1≤i≤p+1, by induction on p+1–i. The base case (i=p+1: ε is a suffix of σ) is obvious, and the final case i=1 yields that s = m1::…::mp::ε is a suffix of σ.
S0 is not consonant II: playing the game
In order to show that S0 is not consonant, let me recall that we will show that player I has a winning strategy in some game GX,X(X, X, U), where X=S0.
We let U be the open cover of X × X consisting of the sets Uσ,|τ| × Uτ,|σ| where σ and τ range over all finite lists of natural numbers (all vertices of the tree S0), where |σ| and |τ| denote the lengths of σ and τ respectively.
This is an open cover: σ is in Uσ,|τ|, because σ is not below any leaf of Tσ,|τ|, and similarly τ is in Uτ,|σ|, so (σ, τ) is in Uσ,|τ| × Uτ,|σ|.
M. de Brecht builds player I’s strategy by describing it, and then showing that it has the right properties. The proof is subtler than its short length might suggest. I also find it useful to have an explicit list of the invariants we need to maintain from round i–1 to round i in the game, and here they are. At the end of round i (assuming that those properties already hold with i–1 in place of i at the end of round i–1), we will establish that:
- the elements of xi (as a sequence of natural numbers) are smaller than or equal to |yi|;
- the elements of yi are smaller than or equal to |xi|;
- there are two distinct natural numbers ni, n’i≤|yi| such that every point below ni::xi, as well as every point below n’i::xi, is in Ui;
- every pair (σ, τ) of finite sequences σ and τ such that (xi, yi) is in Uσ,|τ| × Uτ,|σ| must be below (xi, yi).
Invariants 1 and 2 are they key trick, and will be enforced, not by making sure that the elements of xi and yi are small enough, rather by making xi and yi long enough, as sequences of natural numbers. Invariant 3, or at least the existence of one natural number ni≤|yi| such that ↓(ni::xi) is included in Ui, will be required to make sure that the points xi we will build are in Ui–1 (see below); the existence of a second natural number n’i will only be important at the very end of the proof. Invariant 4 will be a consequence of invariants 1 and 2, using property (A), and will be an important property in order to show that player I’s strategy is winning.
With all that said, here is how M. de Brecht’s strategy proceeds. At the start of round i (i≥1), player I is given an open rectangle Ui–1 × Vi–1, not included in any rectangle of the form Uσ,|τ| × Uτ,|σ| but containing (xi–1, yi–1). The latter pair is well-defined if i≥2, as this is the pair produced by player I at turn number i–1. If i=1, we agree to define (x0, y0) as (ε, ε), so that we do not have to make a case distinction later. Also, we are informed that the invariants 1–4 hold at the end of round i–1. (Initially, invariants 1, 2 and 4 are certainly satisfied, pretty vacuously, at the “end of round i–1″ with i=1. Invariant 3 is also satisfied, for any choice of n0 and of n’0.) Let us enter round i≥1:
- By invariant 3 at the end of round i–1, there is a natural number ni–1≤|yi–1| such that every point below ni::xi is in Ui; By (B), yi–1 has infinitely many successors n::yi–1 such that ↓(n::yi–1) is entirely included in Vi–1. We pick one of them. Player I then decides to play xi ≝ 0n::ni–1::xi–1.
Notice that xi is in Ui–1, thanks to invariant 3. - Now player II plays an open neighborhood Ui of xi included in Ui–1, over which player I has no control.
- By (B), xi has infinitely many successors whose downward closure is entirely included in Ui. We pick two of them, p::xi and q::xi, with p≠q and both p and q larger than or equal to ni–1. Player I then decides to play yi ≝ 0p+q::n::yi–1. (The number n was picked two bullet points above. The numbers p and q will be the ni and n’i needed to establish invariant 3. M. de Brecht chooses p+q as the exponent, but max(p,q) would be enough: the only requirement here is that p, q should both be smaller than or equal to |yi|, as we will see below.)
Notice why yi is in Vi–1: the way we have picked n was so that ↓(n::yi–1) is entirely included in Vi–1, so adding any number of zeroes in front of n::yi–1, however large that may be, will still produce a point in Vi–1. - Player II plays an open neighborhood Vi of yi included in Vi–1, over which player I still has no control.
Note how the invariants are maintained:
- The elements of xi are those of xi–1, which are all smaller than or equal to |yi–1| by invariant 1 at the end of round i–1, plus ni–1 and 0. Since yi–1 is a suffix of yi, we have |yi–1|≤|yi|; 0 is smaller than or equal to any number, and ni–1≤p≤|yi|. Therefore all the elements of xi are smaller than or equal to |yi|.
- The elements of yi are those of yi–1, which are all smaller than or equal to |xi–1| (hence to |xi|) by invariant 2 at the end of round i–1, plus n and 0. But xi = 0n::ni–1::xi–1, so in particular n≤|xi|. It follows that all the elements of yi are smaller than or equal to |xi|.
- The number p was chosen so that ↓(p::xi) is entirely included in Ui. Also, p≤|yi|. We can therefore take ni ≝ p. Similarly, we take n’i ≝ q, since ↓(q::xi) is entirely included in Ui and q≤|yi|.
- Let us imagine that (xi, yi) is in an open rectangle of the form Uσ,|τ| × Uτ,|σ|. Since xi–1 is above xi and yi–1 is above yi, (xi–1, yi–1) is also in Uσ,|τ| × Uτ,|σ|. Hence, by invariant 4 at the end of round i–1, (xi–1, yi–1) is above (σ, τ). In particular (and this is the only thing we will use the latter for), |yi–1|≤|τ|≤|σ|+|τ|.
By invariant 1 (at the end of round i–1), the elements of xi–1 are all less than or equal to |yi–1|. The only additional non-zero element in xi is ni–1, which is less than or equal to |yi–1| as well, by invariant 3. Therefore all the elements of xi are less than or equal to |yi–1|, hence to |σ|+|τ|. By property (A), it follows that xi is above σ.
In particular, |xi|≤|σ|≤|σ|+|τ|. By invariant 2 (at the end of round i this time), all the elements of yi are smaller than or equal to |xi|, hence to |σ|+|τ|. We can therefore use property (A) once more, and conclude that yi is above τ. This allows us to conclude that (xi, yi) is above (σ, τ).
We now need to show that Ui × Vi cannot be included in any rectangle of the form Uσ,|τ| × Uτ,|σ|. We reason by contradiction. Let us imagine that Ui × Vi ⊆ Uσ,|τ| × Uτ,|σ|, for some finite lists of natural numbers σ and τ. Since (xi, yi) is in Ui × Vi, it is in Uσ,|τ| × Uτ,|σ|, and therefore, by invariant 4, (xi, yi) is above (σ, τ).
This is the place where we need the two successors ni::xi and n’i::xi of xi guaranteed by invariant 3. Invariant 3 tells us that the downward closure of each one is included in Ui. In particular, both ni::xi and n’i::xi are in Ui, hence in Uσ,|τ|. All the elements of xi are smaller than or equal to |yi| by invariant 1, hence to |τ|≤|σ|+|τ|, since yi is above τ. Invariant 3 also tells us that ni, n’i ≤ |yi|, hence they are also both less than or equal to |σ|+|τ|. By property (A), it follows that both ni::xi and n’i::xi are above σ. In other words, they are both suffixes of σ. But that is impossible, since ni≠n’i.
This allows us to conclude that Ui × Vi cannot be included in any rectangle of the form Uσ,|τ| × Uτ,|σ|, at any round i. Therefore the strategy for player I we have described above is winning, and this completes our argument that S0 is not consonant.
- Matthew de Brecht. Some results on countably based consonant spaces. Recent Developments in General Topology and its Related Fields, RIMS Kôkyûroku No. 2151, 2019.
- Till Plewe. Localic products of spaces. Proceedings of the London Mathematical Society, Volume s3-73, Issue 3, November 1996, Pages 642–678, https://doi.org/10.1112/plms/s3-73.3.642
- Ruiyuan Chen. Products of Scott topologies and spatiality. Note, last consulted February 19th, 2023.
- Ruiyuan Chen. A geometric proof that S0 × S0 is not spatial. Note, last consulted February 19th, 2023.

— Jean Goubault-Larrecq (February 20th, 2023)