A funny convergence of topics happened a few weeks ago. Frédéric Mynard asked me whether I knew the name of a certain kind of topological spaces which had cropped up in this research. I did not. Later he told me that those were the strongly sober spaces, as introduced in the classic red book [1, Definition VI-6.12]. Oops! That had vaguely rung a bell, but I had completely forgotten about them.
At the same time, I was writing a chapter of my next book, on spaces of lenses and other variants of the Plotkin powerdomain, and I had just realized that one could generalize some results due to Reinhold Heckmann [2] and to myself [3] to so-called weakly Hausdorff spaces, as introduced by Klaus Keimel and Jimmie Lawson [4, Lemma 6.6]. The two notions seemed to have something in common, and indeed they have! I would like to explain what.
Weakly Hausdorff spaces
There are several notions of “weakly Hausdorff space” in the literature, so let me stress that I am considering the notion introduced by Keimel and Lawson in [4, Lemma 6.6].
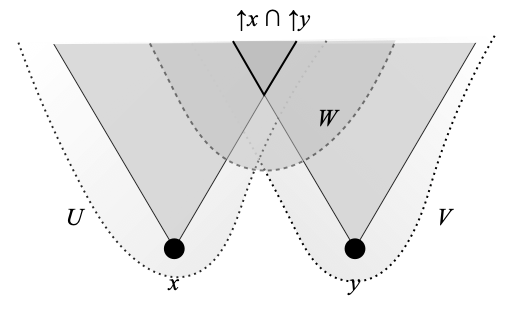
A space X is weakly Hausdorff (in their sense) if and only if:
- for any two points x and y in X,
- for every open neighborhood W of ↑x ∩ ↑y,
- there is an open neighborhood U of x and there is an open neighborhood V of y
- such that U ∩ V ⊆ W.
The following picture may help.
It is clear that every Hausdorff space is weakly Hausdorff: either x=y and we can take U and V both equal to W, or x≠y and we can even require that U ∩ V be empty. In fact, a T1 space is Hausdorff if and only if it is weakly Hausdorff.
Keimel and Lawson then observe that there is another, distinct class of spaces that are weakly Hausdorff:
Fact [4, Lemma 8.1]. Every stably locally compact space X is weakly Hausdorff .
A stably locally compact space is a locally compact, coherent, sober space (see Section 8.3.3 of the book).
Proof. Let x and y be any two points of X, and W be an open neighborhood of ↑x ∩ ↑y. We consider the collection F of sets of the form Q ∩ Q’, where Q is a compact saturated neighborhood of x and Q’ is a compact saturated neighborhood of y.
Since X is coherent, any intersection of two compact saturated neighborhoods of a point is again a compact saturated neighborhood of that point (that is the definition of coherence); so F is closed under binary intersections. Since X is locally compact, for every open neighborhood U of x and for every open neighborhood V of y, U contains a compact saturated neighborhood Q of x and V contains a compact saturated neighborhood Q’ of y, so U ∩ V contains an element of F. In particular, with U and V both equal to X, we find that F is non-empty. This also implies that the intersection of all the elements of F is the intersection of all the open neighborhoods U of x (namely, ↑x) intersected with the intersection of all the open neighborhoods V of y (namely, ↑y). Since X is coherent (once again), every element Q ∩ Q’ of F is compact saturated. Hence we have a filtered intersection of compact saturated sets, equal to ↑x ∩ ↑y, hence included in W.
Since X is well-filtered (every sober space is well-filtered, see Proposition 8.3.5 of the book), one of those elements Q ∩ Q’ is included in W. It remains to take the interior of Q for U and the interior of Q’ for V: U contains x, V contains y, they are open, and their intersection is included in W. ☐
I would like to mention that there is yet a third class of weakly Hausdorff spaces: all preordered sets with their Alexandroff topology. Indeed, for every open neighborhood W of ↑x ∩ ↑y, we can simply define U as ↑x, V as ↑y, and you have it: an open neighborhood U of x, an open neighborhood V of y, and U ∩ V ⊆ W.
Locally strongly sober spaces
The strongly sober spaces that Frédéric Mynard was interested in are defined in terms of convergence of ultrafilters, as well as the slightly more general class of locally strongly sober spaces, which I will be more interested in here. The strongly sober spaces turn out to simply be the compact, locally strongly sober spaces.
An ultrafilter U is a filter (of subsets of a space X) such that for every subset A of X, either A or its complement is in U. In general, a filter converges to a point x (i.e., x is a limit of the filter) if and only if every open neighborhood of x is in the filter. I will write lim U for the set of limits of U.
A space is locally strongly sober if and only if for every ultrafilter U, lim U is empty or is the closure ↓z of a unique point z. (For strongly sober spaces, only the second possibility is allowed.)
It turns out that all Hausdorff spaces, and all stably locally compact spaces, are locally strongly sober. For Hausdorff spaces, this is because ultrafilters (and in fact all filters) have at most one limit. I will give a proof for stably locally compact spaces near the end of this post, rather different from the argument one obtains from Proposition VI-6.15 and Corollary VI-6.16 of [1].
Hence we have two kinds of spaces, the weakly Hausdorff spaces and the locally strongly sober, which both appear to generalize the same three categories of spaces (Hausdorff spaces, stably locally compact spaces). Is there any relationship between those two?
Locally strongly sober implies weakly Hausdorff
That was of course a rhetorical question. We start with the following implication. It will be useful to remember the following result (Lemma B there): for every ultrafilter U, lim U is the intersection of the closures of sets A in U (or equivalently, of all closed sets that are in U). For now, we will only use this to say that for every closed set C in U, every limit of U is in C, but we will need it in full later.
Lemma A. Every locally strongly sober space is weakly Hausdorff.
Proof. Let X be a locally strongly sober space, x, y ∈ X, and let W be an open neighborhood of ↑x ∩ ↑y. Let also C ≝ X–W. For the sake of contradiction, we assume that there is no pair of an open neighborhood U of x and of an open neighborhood V of y such that U ∩ V ⊆ W. For all those pairs, U ∩ V ∩ C is non-empty, and therefore they form a so-called filter base, namely a filtered collection of non-empty sets. By taking the upward closure of this filter base, we obtain a (proper) filter, and a standard use of Zorn’s Lemma shows that any (proper) filter is included in some maximal (proper) filter; and the latter are the same thing as ultrafilters.
Hence, let U be any ultrafilter containing the filter base of sets U ∩ V ∩ C as above. Every open neighborhood of x is in U, so x ∈ lim U. Similarly, y ∈ lim U. Since lim U is non-empty, by assumption there is a point z ∈ X such that lim U = ↓z. Now, on the one hand, x and y are in lim U = ↓z, so z ∈ ↑x ∩ ↑y ⊆ W. On the other hand, C is closed and in U, so every limit of U is in C. In particular z is in C, and that is impossible since z is in W. ☐
At this point, you may wonder whether we could prove the converse, right? Namely, is every weakly Hausdorff space locally strongly sober?
Locally strongly sober space implies sober, coherent
Well, no… weak Hausdorffness and local strong sobriety are not the same property. Locally strong sober spaces have additional properties. The first one is expected, considering the name. It is time to recall that a sober space is a space in which every irreducible closed set is the downward closure of a unique point (Definition 8.2.4 in the book), where a closed set C is irreducible if and only if it is non-empty and is such that if C intersects two open sets U and V, then it also intersects U ∩ V (Trick 8.2.3 in the book).
Lemma B (Lemma VI-6.13 in [1]). Every locally strongly sober space is sober.
Proof. Let C be an irreducible closed set in a locally strongly sober space X. Let F be the collection of intersections U ∩ C of an open set U with C that are non-empty. Since C is non-empty, C = X ∩ C is in F. If U ∩ C and V ∩ C are in F, namely if both U and V are open sets that intersect C, then their intersection also intersects C, by irreducibility; so (U ∩ C) ∩ (V ∩ C) is non-empty, and therefore in F. This means that F is a filter base. Let U be any ultrafilter containing F. Since X is locally strongly sober, lim U is equal to ↓z for a unique point z.
C is closed and in U, so z, being a limit of U, is in C. Therefore ↓z is included in C. Conversely, for every point x of C, every open neighborhood U of x intersects C, so U ∩ C is in F, hence also in U; in other words, every point of C is a limit of U, hence is in ↓z. Therefore C=↓z, and the point z is unique, so X is sober. ☐
In comparison, not all weakly Hausdorff spaces are sober. (For example, the set N of natural numbers, with the cofinite topology, is not sober, because it is itself an irreducible closed set. But, as a T1 space, it is weakly Hausdorff. Oops! Wrong counterexample: spotted by Xiaodong Jia on November 20th, 2022. The next one should be right, and is the one I am using in [5, Example 4.7].) Consider Nω, the set of natural numbers plus a fresh element ω, ordered by 0 < 1 < … < ω, in its Alexandroff topology. Being Alexandroff, it is weakly Hausdorff. Not all its open subsets are Scott-open: {ω} is open, however ω=sup {n | n ∈ N} is in it and no n ∈ N is in it. Hence Nω is not a monotone convergence space; a space is monotone convergence if and only if it is a dcpo in its specialization ordering, and every open set is Scott-open. Every sober space is monotone convergence (Proposition 8.2.34 in the book). Therefore Nω is not sober. Explicitly, N is closed in Nω, and is irreducible, but is not the downward closure of any point.
Sobriety is still not enough.
Lemma C (Lemma VI-6.14 in [1]). Every locally strongly sober space is coherent.
Proof. Let Q, Q’ be two compact saturated subsets of a locally strongly sober space X. We wish to show that Q ∩ Q’ is compact (and saturated, but that is clear). If Q ∩ Q’ is empty, that is obvious, so we assume that it not empty. Let us consider any ultrafilter U containing Q ∩ Q’. U contains Q, and we have seen that lim U is equal to the filtered intersection of the closed sets C in U. For each such closed set C, since C is in U, and since Q contains Q ∩ Q’ hence is also in U, C ∩ Q is in U as well, hence cannot be empty. Therefore every closed set C in U intersects Q, so the intersection lim U of all those closed sets also intersects Q, since Q is compact. In particular, lim U is non-empty, so it is equal to ↓z for some point z in X. Since lim U=↓z intersects Q and Q is saturated, z is in Q. Similarly, lim U intersects Q’, so z is in Q’. It follows that z is in Q ∩ Q’, so lim U intersects Q ∩ Q’.
We have just shown that every ultrafilter U containing Q ∩ Q’ converges to some point of Q ∩ Q’. This is the ultrafilter-based definition of the fact that Q ∩ Q’ is compact. For a non-ultrafilter based proof, let (Ui)i ∈ I be any directed family of open sets whose union contains Q ∩ Q’, and let us assume, for the sake of contradiction, that none of them contains Q ∩ Q’. Then the complements Ci of Ui all intersect Q ∩ Q’, so the sets Ci ∩ Q ∩ Q’ form a filter base. By Zorn’s Lemma, there is an ultrafilter U containing all those sets. U contains Q ∩ Q’, so lim U intersects Q ∩ Q’, as we have shown above. But lim U is the intersection of all closed sets in U, and is therefore included in the intersection ∩i ∈ I Ci. This show that ∩i ∈ I Ci intersects Q ∩ Q’, contradicting the fact that (Ui)i ∈ I is an open cover of Q ∩ Q’. ☐
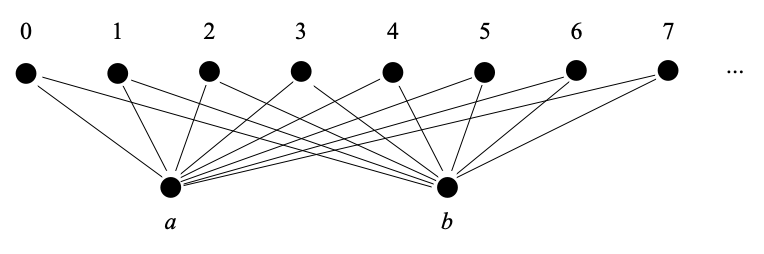
And there are weakly Hausdorff spaces, even sober ones, that are not coherent. Xiaodong Jia proposed the following as an example of this situation. We have already mentioned this space as Na,b here.
This is obtained as the union of N with two new elements a and b below all natural numbers; a and b are incomparable, and all natural number are pairwise incomparable. We give this poset its Scott topology, or equivalently its Alexandroff topology. This is weakly Hausdorff because it is a poset with its Alexandroff topology. It is sober, and you can see this, for example, by realizing that this is an algebraic domain, and that all algebraic domains are sober in their Scott topology. It is not coherent, because ↑a ∩ ↑b is the whole of N, which is not compact.
Weakly Hausdorff + coherent + sober = locally strongly sober
But that is all we need!
Theorem. The locally strongly sober spaces are exactly the weakly Hausdorff, coherent, sober spaces. More precisely, it is equivalent for a topological space X to be:
- locally strongly sober;
- or weakly Hausdorff, weakly coherent, and a monotone convergence space;
- or weakly Hausdorff, coherent, and sober.
One term is undefined in the above statement: I will say that a space is weakly coherent if and only if ↑x ∩ ↑y is compact for every pair of points x and y. The notion was already used in the post on the Jia-Jung-Li theorem, where I had not given it any name. Clearly, every coherent space is weakly coherent.
Proof. The implication 1 ⇒ 3 is the conjunction of Lemmata A, B, and C above. The implication 3 ⇒ 2 is clear. We concentrate on 2 ⇒ 1. Hence, let X be a weakly Hausdorff, weakly coherent monotone convergence space.
Let U be an ultrafilter on X, and let us assume that lim U is non-empty. For any two points x, y ∈ lim U, ↑x ∩ ↑y is compact since X is weakly coherent. Let us assume that ↑x ∩ ↑y does not intersect lim U. Since lim U is the filtered intersection of the closed sets C in U, and using compactness, ↑x ∩ ↑y ∩ C must be empty for some closed set C in U. Let W be the complement of C; so ↑x ∩ ↑y ⊆ W. By weak Hausdorffness, there are an open neighborhood U of x and an open neighborhood V of y such that U ∩ V ⊆ W. Since x ∈ lim U, U is in U, and similarly V is in U; therefore U ∩ V, and then also the larger set W, is in U. But C is in U, and that would entail that W ∩ C would be in U; that is impossible, since W ∩ C is empty.
This shows that lim U is directed. Since X is a monotone convergence space, lim U has a supremum z, and z ∈ lim U because lim U is closed (hence Scott-closed). Every closed set is downwards-closed, so lim U = ↓z. The uniqueness of z follows from the fact that every monotone convergence space is T0. ☐
Stably locally compact spaces
I had promised that I would give a proof of the fact that all stably locally compact spaces are locally strongly sober, and a rather different one from the argument one obtains from Proposition VI-6.15 and Corollary VI-6.16 of [1]. Here it is.
Lemma. Every stably locally compact space is locally strongly sober.
Proof. By the first Fact seen in this post, every stably locally compact space is weakly Hausdorff. It is coherent and sober by definition. By the Theorem we have just proved, it is locally strongly sober. ☐
We also have the following characterization of stably locally compact spaces, as a conjunction of pretty weak properties.
Theorem. The stably locally compact spaces are exactly the core-compact, weakly Hausdorff, weakly coherent, monotone convergence spaces.
Proof. One direction follows from the implications locally compact ⇒ core-compact, coherent ⇒ weakly coherent, sober ⇒ monotone convergence, and stably locally compact ⇒ weakly Hausdorff. Conversely, let X be a core-compact, weakly Hausdorff, weakly coherent, monotone convergence space. By the previous Theorem, X is coherent and sober. Being sober and core-compact, it is locally compact (Theorem 5.2.9 in the book). ☐
This way, we retrieve the following result.
Corollary (Proposition VI-6.16 [1]). The stably locally compact spaces are exactly the core-compact (equivalently, locally compact) locally strongly sober spaces.
Adding compactness to the mix, the stably compact spaces are exactly the core-compact (equivalently, locally compact) strongly sober spaces.
Sobriety and monotone convergence
Every weakly Hausdorff, weakly coherent monotone convergence space is locally strongly sober, hence coherent and sober. Without any kind of coherence property, we still have the following.
Proposition. For a weakly Hausdorff space, monotone convergence and sobriety are equivalent properties.
Proof. We only have to show that every weakly Hausdorff monotone convergence space X is sober. Let C be an irreducible closed subset of X. For any two points x, y of C, if ↑x ∩ ↑y were included in the complement W of C, then W would contain an intersection U ∩ V of an open neighborhood U of x and of an open neighborhood V of y. Since C is irreducible, U ∩ V , and therefore also W would intersect C, but that is impossible. Hence ↑x ∩ ↑y intersects C. This shows that C is directed. Since X is a monotone convergence space, z ≝ sup C exists and is in C, so C=↓z. Since X is T0, z is unique, and therefore X is sober. ☐
Coherence
Similarly, without any need for monotone convergence or sobriety, we have the following.
Proposition. For a weakly Hausdorff space, weak coherence and coherence are equivalent properties.
Proof. (Update, November 21st, 2022: the proof I had given was for an entirely different property. Thanks to Xiaodong Jia for spotting this! I have a policy of not removing anything after posting, even if it is a blatantly silly mistake. I have therefore put the former proof—which actually proves something interesting—in Appendix A.)
Let Q1, Q2 be two compact saturated subsets of X, and let (Wi)i∈I be an open cover of Q1 ∩ Q2. For each pair (x,y) ∈ Q1 ∩ Q2, ↑x ∩ ↑y is included in Q1 ∩ Q2, hence in ∪i∈I Wi. Since X is weakly coherent, there is a finite subset Jxy of I such that ↑x ∩ ↑y ⊆ ∪i∈Jxy Wi. Since X is weakly Hausdorff, x has an open neighborhood Ux and y has an open neighborhood Vy such that Ux ∩ Vy ⊆ ∪i∈Jxy Wi. The sets Ux, x ∈ Q1, form an open cover of Q1, so there is a finite subset E1 of Q1 such that Q1 ⊆ ∪x∈E1 Ux. Similarly, there is a finite subset E2 of Q2 such that Q2 ⊆ ∪y∈E2 Vy. Then the sets Wi, where i ∈ ∪x∈E1, y∈E2 Jxy, form a finite subcover of Q1 ∩ Q2. ☐
This sounds a lot like the Jia-Jung-Li theorem, which states that every well-filtered dcpo in its Scott topology that is weakly coherent is coherent.
But the assumptions of the Jia-Jung-Li theorem seem rather different from weak Hausdorffness. For example, consider Isbell’s non-sober complete lattice L. L is well-filtered, by the Xi-Lawson theorem. It is also weakly coherent, because every complete lattice is, trivially. Hence it is coherent, by the Jia-Jung-Li theorem. However, it is not weakly Hausdorff, otherwise it would be locally strongly sober, hence sober.
I have said in the introduction that I came to rely on weak Hausdorffness in order to obtain new results (with simpler proofs) on spaces of lenses. Let me postpone that to another time… or read the arXiv report [5], which also contains some additional information (examples, and a characterization of the Stone duals of locally strongly sober spaces, most notably).
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- Reinhold Heckmann. Abstract Valuations: A Novel Representation of Plotkin Power Domain and Vietoris Hyperspace. Proceedings of the 13th International Symposium on Mathematical Foundations of Programming Semantics (MFPS’97). Stephen Brookes and Michael Mislove, editors. Electronic Notes in Theoretical Computer Science 6, 1997.
- Jean Goubault-Larrecq. De Groot duality and models of choice: angels, demons and nature. Mathematical Structures in Computer Science , Volume 20 , Special Issue 2: Domains , April 2010 , pp. 169 – 237. doing: https://doi.org/10.1017/S0960129509990363
- Klaus Keimel and Jimmie Lawson. Measure extension theorems for T0-spaces. Topology and its Applications, 149(1–3), 57–83, 2005.
- Jean Goubault-Larrecq. On weakly Hausdorff spaces and locally strongly sober spaces. arXiv report 2211.10400, November 21st, 2022.

— Jean Goubault-Larrecq (November 20th, 2022)
Appendix A
As I said in the main text, I had initially given a wrong proof of the last Proposition. In fact, it showed the following, which is an equivalent characterization of weakly Hausdorff spaces, as given in [4, Lemma 6.6].
Fact. A space X is weakly Hausdorff if and only if:
- for any two compact saturated subsets Q1 and Q2 in X,
- for every open neighborhood W of Q1 ∩ Q2,
- there is an open neighborhood U of Q1 and there is an open neighborhood V of Q2
- such that U ∩ V ⊆ W.
Proof. The if direction follows by taking Q1 equal to ↑x and Q2 equal to ↑y. In the only if direction, we assume that X is weakly Hausdorff. Let us define an orthogonality relation ⊥ between compact saturated sets by Q1 ⊥ Q2 if and only if every open neighborhood W of Q1 ∩ Q2 contains an intersection U ∩ V of an open neighborhood U of Q1 and of an open neighborhood V of Q2. By assumption, ↑x ⊥ ↑y for all points x, y ∈ X. Let us say that a compact saturated set Q is good if and only if it is orthogonal to every compact saturated set, and pretty good if and only if it is orthogonal to every set of the form ↑y, y ∈ X.
We claim that every pretty good set Q1 is good. In order to show this, we consider any compact saturated set Q2, and any open neighborhood W of Q1 ∩ Q2; we must find an open neighborhood U of Q1 and an open neighborhood V of Q2 such that U ∩ V ⊆ W. For each y ∈ Q2, since Q1 is pretty good, there is an open neighborhood Uy of Q1 and an open neighborhood Vy of y such that Uy ∩ Vy ⊆ W. Since Q2 is compact, there is a finite subset E of Q2 such that Q2 ⊆ V ≝ ∪y∈E Vy. Let U ≝ ∩y∈E Uy. Then U is an open neighborhood of Q1, and U ∩ V ⊆ W, as desired.
By assumption, every set of the form ↑x is pretty good, hence good. This means that ↑x ⊥ Q for every compact saturated set Q, for every x ∈ X. In other words, every compact saturated set Q is pretty good; hence every compact saturated set is good. ☐