The space S0

The space S₀ originates from a deep paper of Matthew de Brecht’s on a characterization of quasi-Polish spaces by forbidden substructures [1]. Namely, his theorem (Theorem 7.2 in [1]) says that a coanalytic subspace of a quasi-Polish space will always be quasi-Polish unless it embeds one of four possible forbidden substructures as Π²₀-subspaces. I will not explain what this all means, except that the four possible substructures in question, which de Brecht calls S₀, S₁, S₂ and S_D, are well-known, except for the first one. S₁ is the T₁ space of natural numbers with the cofinite topology, S₂ is the T₂ space of rational numbers with its usual, metric topology, S_D is the T_D space of natural numbers with the Alexandroff (or Scott) topology of its usual ordering. S₀ is a T₀ space, as you may have guessed, but does not seem to have appeared earlier in the literature.

A few years ago, Matthew de Brecht was visiting my university, and tried to get me interested in S₀, and in particular to try to discover whether S₀ was consonant or not. I had a hard time understanding the properties of S₀, and I was unable to contribute. I was sure he managed to show that S₀ is not consonant, but the paper where I expected to find it [2] makes no mention of consonance at all. If I can sort this out, I will try to explain the answer to the question on this blog. In any case, now I understand S₀ a bit better, and I would like to explain what I know about it.

The definition of S₀

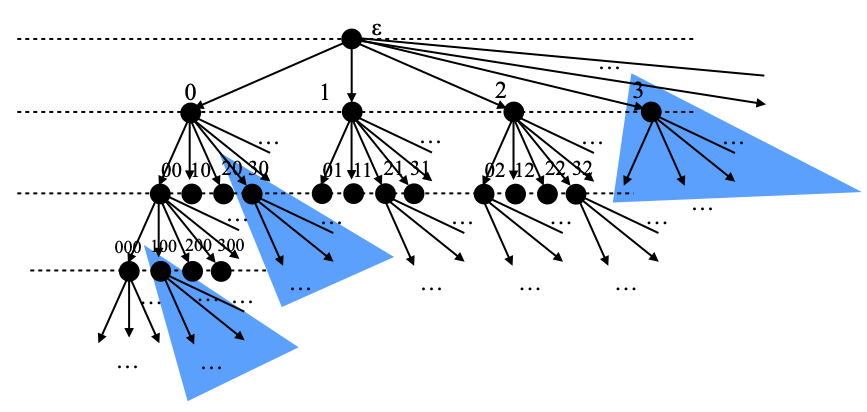
Right, so, here is the definition (not quite the same as in [1], which uses prefixes instead of suffixes, but the space we will obtain will be homeomorphic). S₀ is the space of finite sequences of natural numbers, with the upper topology of the (opposite of the) suffix ordering.

Let me explain this more slowly. I will write ε for the empty sequence, n::s for the sequence obtained by adding a natural number n in front of a sequence s, and n₁…n_k for the sequence of natural numbers n₁, …, n_k. In particular, n₁…n_k = n₁::(n₂…n_k) if k≥1, and in general n₁…n_k = n₁::(n₂:: … (n_k::ε)…).

A suffix of a finite sequence n₁…n_k is any finite sequence n_p…n_k, where 1≤p≤k+1 (if p=k+1, this denotes the empty sequence). Let me write s≤t if t is a suffix of s. This is the (opposite of the) suffix ordering. Note that S₀ has a largest element, which is the empty sequence ε. Each element s has a countably infinite set of successors n::s, n ∈ N, where is a successor of s is an element immediately below s (i.e., strictly below s and without any other element inbetween). We then see that S₀ is a reversed tree (some vertices and some branches are missing — it’s pretty hard to draw an infinite structure as a finite picture), with root ε:

We equip S₀ with the upper topology of its ordering ≤. This means that the closed subsets of S₀ are the intersections ∩_{i ∈ I} ↓E_i, where each E_i is a finite set. (↓E_i is the downward closure of E_i, hence the set of all sequences that have a suffix in E_i—although one has a better grasp of what they are by imagining what such sets would look like on the picture above. The downwards closed subsets of finite sets are called finitary closed subsets in the book.)

Since there are countable many finitary closed subsets ↓E in S₀, let me note in passing that S₀ is not just countable, but also countably-based.

The closed subsets of S₀

Since S₀ is countable, it has only countably many finitary closed subsets. However, as M. de Brecht notices, it has more. That is, it has closed sets that are non-trivial infinite intersections ∩_{i ∈ I} ↓E_i of finitary closed sets. In fact, it has so many that they form an uncountable set:

Proposition [1, Proposition 6.1]. S₀ has uncountably many closed sets. Equivalently, S₀ has uncountably many open sets.

Proof. It suffices to exhibit an injection from the set N^N of infinite sequences of natural numbers to the collection H(S₀) of closed subsets of S₀.

Given any infinite sequence k≝(k_n)_{n ∈ N} of natural numbers, we form the following points of S₀: first the one-element sequence k₀+1 (namely, the k₀+2nd successor of the root ε), then the two-element sequence (k₁+1)0 (the k₁+2nd successor of the element 0), then the three-element sequence (k₂+1)00 (the k₂+2nd successor of the element 00), and so on. In other words, we look at the leftmost branch of the tree 00…0…, and we pick the k₀+2nd successor of the root, the k₁+2nd successor of the second element from the root on that branch, etc. In general, element number n of that sequence of points is u^k_n ≝ (k_n+1)0ⁿ, where 0ⁿ denotes a sequence of n zeroes. (The superscript k marks the dependence on the initial infinite sequence k.)

We define F_^k as the downward closure of the infinite set {u^k_n | n ∈ N}. For example, here is F_^k when k is the sequence of natural numbers 2, 1, 0, … (again, due to space limitations, I am only showing the downward closures of the first three points u^k₀, u^k₁, and u^k₂). I have shown it in blue:

I claim that F_^k is closed in S₀. To this end, for each natural number n, let E_^kn be the finite set consisting of u_^k0, …, u_^kn, plus the point 0ⁿ⁺¹. On the picture above, and taking n≝2, that would be the collection of the top elements u_^k0, u_^k1, u_^k2 of each of the displayed blue regions, plus the point 000 at the bottom left of the picture. It is pretty easy to see that F_^k ≝ ∩_{n ∈ N} ↓E_^kn, and therefore F_^k is closed.

It is also easy to see that the map k ↦ F_^k is injective. Let us imagine another infinite sequence k‘≝(k’_n)_{n ∈ N} of natural numbers. Since it is distinct from k, we have k_n≠k’_n for some index n. The points of F_^k of the form …k0ⁿ with k≠0 are exactly those such that k=k_n+1, and similarly, those of F_^k’ of the form …k0ⁿ with k≠0 are those such that k=k’_n+1. Hence, for example, (k_n+1)0ⁿ is in F_^k but not in F_^k’. (And (k’_n+1)0ⁿ is in F_^k’ but not in F_^k.) ☐

So S₀ is a countable space, even a second-countable space, with an uncountable topology. That is not a big deal. The same could be said of the space Q of rational numbers, with its usual topology. M. de Brecht also shows that S₀ is not a T_D space, and I will leave that as an exercise to you. (First read the characterization of closed sets, which will come below.)

Sobriety

We now have:

Proposition. S₀ is sober.

This follows from a pretty useful theorem from Andrea Schalk’s PhD thesis:

Proposition [3, Proposition 1.7]. Every poset P in which every non-empty family has a supremum is sober in its upper topology.

(I have already cited this proposition from Schalk in this post, but not with this level of generality.)

Proof. Since P is a poset, P is T₀ in its upper topology.

Let C be an irreducible closed subset of P. Since C is non-empty, it has a supremum x, by assumption. We claim that x is in C. Otherwise, the complement P–C of C would be an open neighborhood of x, and would therefore contain a basic open set P–↓E containing x, where E is finite. Since P–C contains P–↓E, we must have C ⊆ ↓E. But C is irreducible and ↓E is the finite union of sets ↓y, y ∈ E, so C is included in ↓y for some y ∈ E. That implies that y is an upper bound of C. Since x is the least one, x≤y; but then x is in ↓E as well, contradicting the fact that x is in P–↓E.

Therefore x is the largest element of C, and hence C = ↓x. ☐

We apply this to S₀: given any family F of points of S₀, namely of finite sequences of natural numbers, it should be fairly clear that all of them have a longest common suffix; that suffix is the supremum of F. Then the latter proposition immediately gives us that S₀ is sober.

Being sober, S₀ is a monotone convergence space (Proposition 8.2.34 in the book). This means that:

• S₀ is a dcpo with respect to its specialization ordering, which is the (opposite of the) suffix ordering ≤. But that is equally easy to prove directly: every directed family D in S₀ is trivial, in the sense that one of the elements of D is already its supremum; in other words, that every directed family D has a largest element (not just a sup!). Indeed, since D is non-empty, there is a sequence s in D of smallest length. Given any other sequence t in D, by directedness s and t have a common suffix in D. But since s has minimal length among the sequences in D, that common suffix must be s itself; in other words, s must be a suffix of t, namely t≤s.
• The Scott topology on S₀ is finer than the (upper) topology of S₀. That was obvious, too, since the Scott topology on any poset is always finer than the upper topology (by Proposition 4.2.12 of the book, the upper topology is simply finer than any topology that has the same specialization ordering).

The Scott topology on S₀ is very different than the upper topology. Indeed, as a dcpo, S₀ is extremely nice. It is an algebraic domain, and even more: all its elements are finite! In particular, S₀ is locally compact in its Scott topology; and we will see that it is not locally compact in its upper topology.

Closed subsets of S₀ and finitely branching subtrees

Now, given any closed subset C of S₀, every point of C is below some point in Max C, the collection of maximal points of C. This is a general fact that holds for every Scott-closed subset of any dcpo, hence for every closed subset of a sober space.

In the current setting, there is a simpler argument: for every point s of C, we can simply take shorter and shorter suffixes of s as long as they remain in C; the process must terminate, since lengths cannot decrease for infinitely long, and the last suffix thus obtained is the desired maximal element of C above s.

This even shows that every point s of C is below a unique point of Max C.

In any case, we have just obtained the following:

Lemma A [1, Lemma 6.2]. Every closed subset C of S₀ is the downward closure ↓Max C of its set of maximal elements.

Lemma 6.2 in [1] also states that the subspace topology on Max C is discrete, but I think it is better to understand what kind of set Max C is really like, and discreteness will then be an easy consequence.

Let me call subtree any upwards-closed subset of S₀. The name comes from the fact that any (non-empty) upwards-closed subset of S₀ is indeed a tree, with ε as a root.

A leaf of a subtree T is simply a minimal element of T: an element with no successor. Hence let me simply write Min T for the set of leaves of a subtree T. The elements of T are called its vertices, and those that are not leaves are called internal vertices.

Let me say that a subtree T is finitely branching if and only if every element s of T only has finitely many successors n::s in T.

We state the following for S₀, although it should be clear from the proof that a similar statement holds for any reversed tree with the upper topology (where a reversed tree is any set X with a root ε and a so-called predecessor function p : X–{ε} → X such that for every x in X, there is a natural number k such that p^k(x) is defined and equals ε; the successors of an element y are exactly all those elements x≠ε such that p(x)=y, and the ordering ≤ is the reflexive-transitive closure of the relation “is a successor of”).

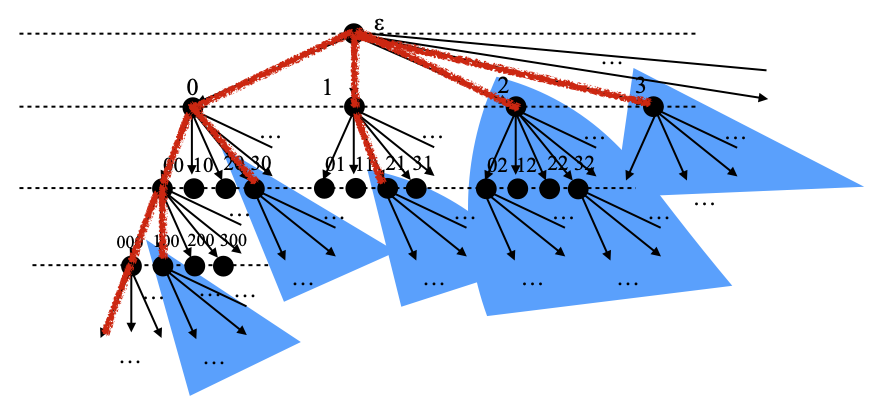
Proposition. For every closed subset C of S₀, ↑Max C is a finitely branching subtree T (which we shall call the canonical tree representative of C), and Min T=Max C. Conversely, for every finitely branching subtree T, ↓Min T is a closed set C and Max C=Min T.

Before I prove this, let me show this in pictures:

The closed set C is displayed in blue (some of the blue regions overlap in that drawing, but really should not, since the downward closures of incomparable points do not intersect in a tree). The corresponding finitely branching subtree T is shown in red, using fuzzy, heavy lines. Note what looks like an infinite branch of T on the left (ε, 0, 00, 000, etc.): I really mean that Max C does not just contain the points 2, 3, 11, 20 and 100 (as shown on the picture), but also infinitely many points ending with arbitrarily long strings of zeroes, e.g., 00001, 000001, 0000001, etc. Assuming that Max C does not contain any string consisting of zeroes only, this creates an infinite branch 00…0… in T. Beware that there is no leaf at the end of an infinite branch!

Proof. Let C be closed in S₀, and T be defined as ↑Max C. T is upwards-closed by definition, hence a subtree. Every leaf of T is in Max C, by construction. Conversely, Max C is an antichain (a set of elements that are pairwise incomparable), so Max C embeds in T as its set of minimal elements. This shows that Min T=Max C.

In order to show that T is finitely branching, let us consider any element of s. If s is a leaf of T, then it has no successor in T, and therefore its set of successors is trivially finite. Let us therefore look at the case where s is an internal vertex of T. Then s is strictly larger than some element of Min T=Max C, and is in particular not in C. By definition of the (upper) topology on S₀, there is a finitary closed set ↓E such that s ∈ S₀–↓E ⊆ S₀–C. By the latter inclusion, C is included in ↓E.

We consider any successor n::s of s that is in T. Since T = ↑Max C, n::s is above some element t ≝ n₁::…::n_k::n::s of Max C. This t is in C, hence in ↓E, namely there is an element u of E that is a suffix of t. This u cannot be a suffix of s, otherwise we would have s≤u, contradicting s ∈ S₀–↓E. Therefore u is of the form n_j::…::n_k::n::s for some j, 1≤j≤k+1 (the case j=k+1 denoting n::s). Since E is finite, there are finitely many possible values of u, hence finitely many possible values of n. This shows that s has only finitely many successors.

Conversely, let T be any finitely branching subtree. We truncate T as follows: for each natural number n, let T_n denote the set of sequences s of length at most n in T. In other words, T_n is the intersection of T with the n+1 topmost levels of S₀ (represented as the dashed horizontal lines in the previous pictures). Since T is finitely branching, an easy induction on n shows that T_n is finite, and therefore also E_n ≝ Min T_n.

We claim that Min T is included in ↓E_n for every n ∈ N. Let indeed s be any leaf of T. If the length of s is at most n, then s is in T_n and, being minimal in T, it is also minimal in T_n, hence is in E_n. If the length of s is strictly larger than n, then its unique length n suffix t is in T and, because it has length exactly n, is minimal in T_n, and is therefore in E_n; since by definition s≤t, s is in ↓E_n. We have therefore shown that Min T, hence also ↓Min T, is included in ∩_{n ∈ N} ↓E_n.

Conversely, let s be any element of ∩_{n ∈ N} ↓E_n. Let n be the length of s. Since s is in ↓E_n+1, s has a suffix t that is a leaf of T_n+1. The length of t is at most n, since t is a suffix of s. Since t is minimal in T_n+1, it has no successor in T_n+1, and therefore no successor in T: so t is minimal in T. This shows that s in in ↓Min T.

It follows that ↓Min T is equal to ∩_{n ∈ N} ↓E_n, and is therefore closed. Since Min T is an antichain, it is clear that the set of maximal elements of C ≝ ↓Min T is exactly Min T. ☐

Are the two constructions, from closed sets C to their canonical tree representative T ≝ ↑Max C, and back from subtrees T to closed sets ↓Min T, inverse of each other? Well, no. Let’s investigate:

• If we start from a closed set C, form its canonical tree representative T ≝ ↑Max C, then C’ ≝ ↓Min T, we have seen that Min T=Max C and Max C’=Min T. So C and C’ are two closed sets with the same set of maximal elements. By Lemma A, they must be equal. Good.
• However, if instead we start from a finitely branching subtree T, form C ≝ ↓Min T, and then T’ ≝ ↑Max C, then similarly T and T’ have the same minimal elements (the same leaves), but the best you can then say is that T’ is included in T. It may fail to be equal to it. The simplest example is given by taking for T a unique infinite branch, say ε, 0, 00, 000, …; then Min T is empty, so C is empty, and then the canonical tree representative T’ is empty, too. The canonical tree representative of a closed set C is simply the smallest subtree T’ such that one can write C as ↓Min T’, not the only one.

From this, it is easy to see the second half of Lemma 6.2 of [1]:

Lemma A [1, Lemma 6.2]. For every closed subset C of S₀, the subspace topology on Max C is discrete.

Proof. Let T be the canonical tree representative of C, so that Min T = Max C. Let s be any element of the latter set, namely, a leaf of T, and let n be the length of s (as a sequence). We will show that there is an open neighborhood U of s such that U ∩ Max C = {s}.

As in the proof of the previous Proposition, let T_n denote the set of sequences s of length at most n in T. Since T is finitely branching, T_n is finite. Let E_n be its set of minimal elements. Every element of Max C = Min T is either of length ≤n and then is in E_n, or of length >n and then strictly smaller than some element u of E_n; in the latter case, u must be different from s, since both u and s are maximal in C. Hence ↓(E_n–{x}) is a closed set that contains all the maximal elements of C, except for x. The desired open set U is the complement of ↓(E_n–{x}). ☐

Oh, before we go on to explore the compact saturated subsets of S₀, please do not think that the canonical tree representative T ≝ ↑Max C of a closed set C is simply the complement of C. First, T intersects C (at Max C). All right, but maybe you would be tempted to say that the set T–Min T of internal vertices of T would be the complement of C. This would be wrong as well. Looking at the previous picture, the complement of C consists not just in those internal vertices (which are, in particular, on red paths), but also all those vertices that have neither a blue nor a red background, and there are plenty of them. In fact, you can check that T–Min T is never open (unless empty).

The compact saturated subsets of S₀

The compact saturated subsets Q are also subtrees… since we have simply defined subtrees as upwards-closed (=saturated) subsets. Instead of being finitely branching, those are well-founded, namely: there is no infinitely strictly descending chain in Q.

Again, the following would hold in any tree. The funny thing is that there is something called König’s Lemma, which states that every finitely branching well-founded tree is finite. Here we have to choose: closed sets are described by finitely branching trees (in general not well-founded), and compact saturated sets are well-founded trees (in general not finitely branching).

Proposition. The compact saturated subsets of S₀ are exactly its well-founded subtrees.

Proof. Let Q be a compact saturated subset of S₀. Let us imagine that there were an infinite strictly descending chain s₀ > s₁ > … > s_n > … in Q. The sets ↓s_n, where n ranges over N, form a filtered family of closed sets, which all intersect Q. Since Q is compact, the intersection ∩_{n ∈ N} ↓s_n must also intersect Q. But that is absurd, since ∩_{n ∈ N} ↓s_n is empty: any word in that intersection would need to be longer than any s_n, and the lengths of the sequences s_n are not bounded.

Conversely, let T be a well-founded subtree. We claim that T is compact. (It is saturated, being a subtree.) By Alexander’s Subbase Lemma (Theorem 4.4.29 in the book), it suffices to show that, given any family of subbasic open sets (here, of the form S₀–↓s_i, for single points s_i; I will let i range over some index set I, too) whose union contains T, a finite sub-union already contains T. Our assumption rewrites as saying that T does not intersect ∩_{i ∈ I} ↓s_i. We wish to show that T is included in some finite union of sets S₀–↓s_i, or equivalently, that T fails to intersect some finite intersection of sets of the form ↓s_i.

That is obvious if some s_i is already outside T, since T is upwards-closed, so let us assume that every s_i is in T. That is also easy if we can find two incomparable points s_i and s_j, for some i, j in I. In that case, and because S₀ is a tree, ↓s_i ∩ ↓s_j is empty, so T will certain fail to intersect it. Hence we may assume that not only every s_i is in T, but also that they are all comparable, in other words, that they lie on the same branch of the tree S₀. If there were infinitely many distinct elements s_i, they would form an infinite descending chain; but those do not exist, since T is well-founded. Therefore there are only finitely many points s_i, i ∈ I. One of them, say s_k, is then the smallest among them, and hence ∩_{i ∈ I} ↓s_i = ↓s_k. Since T intersects ∩_{i ∈ I} ↓s_i (by assumption), it also intersects ↓s_k, and we are done. ☐

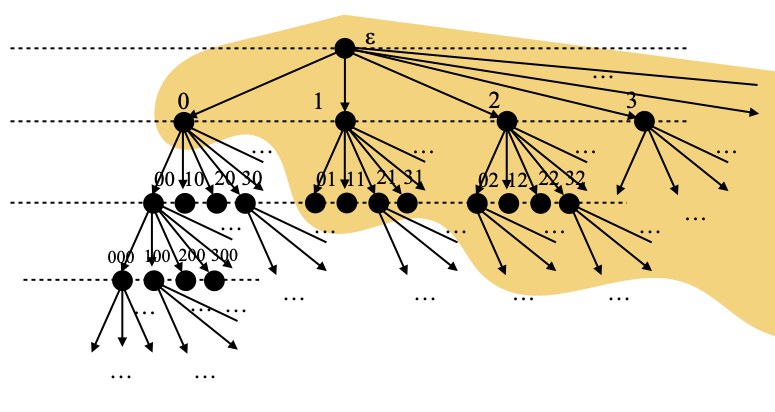
By the way, a well-founded subtree is not the same thing as a bounded subtree, namely a subtree whose elements have bounded length. Here is an example of a well-founded subtree in S₀ that exhibits the difference. The orange region is a well-founded subtree, whose leaves (minimal elements) are 0, then all the 2-element sequences of the form n::1, n ∈ N, then all the 3-element sequences of the form n::m::2, and so on.

S₀ is not locally compact

We remember that closed sets C are such that T ≝ ↑Max C is a finitely branching tree. It follows that, given any non-empty open subset U of S₀, U has at least one infinite branch. (In fact, it has uncountably many). Equivalently, if C is a proper closed subset of S₀, then there is an infinite branch in S₀ that avoids C entirely. We argue as follows. Since C is proper, namely different from the whole of S₀, ε is not in C. Now ε only has finitely many successors in T, but infinitely many in S₀, so we can pick one that is not in T, say n::ε.

We claim that no point u below n::ε can be in C. Otherwise, u would be below some point v in Max C (by Lemma A), namely, v would be a suffix of u. Since u is a sequence ending in n::ε (i.e., having it as a suffix), either v=ε or v ends in n::ε as well. But, if v=ε, and since v is in Max C, ε would be in C, which is impossible. Hence v has n::ε as a suffix, meaning that v≤n::ε. Since v is in Max C, this would entail that n::ε is in T = ↑Max C, which is also contradictory.

Hence any infinite branch starting with ε and n::ε will avoid C entirely.

Proposition. Every compact saturated subset of S₀ has empty interior. In particular, S₀ is not locally compact.

Proof. Let Q be a compact saturated subset of S₀, and let U be any non-empty open subset of S₀. We have just argued that, since U is non-empty, it contains an infinite branch. Since all the branches in Q are finite, some element on that infinite branch must be outside Q. Hence U is not included in Q. In other words, the only open subset included in Q is the empty set, so Q has empty interior. ☐

S₀ is Choquet-complete

Let me recall from Section 7.6 of the book that the strong Choquet game on a space X is played between two players, α and β. Player β starts the game by picking a point x₀ and an open neighborhood V₀ of x₀. Then α replies with an open neighborhood U₀ of x₀ included in V₀; β picks a possibly different point x₁ in U₀, an open neighborhood V₁ of x₁ included in U₀; α replies with an open neighborhood U₁ of x₁ included in V₁; β picks a possibly different point x₂ in U₁, an open neighborhood V₂ of x₂ included in U₁, and so on. After both players have played for as many turns as there are natural numbers, α is declared to win if ∩_{n ∈ N} U_n (which is also equal to ∩_{n ∈ N} V_n) is non-empty. Otherwise, β wins.

The space X is Choquet-complete if and only if α has a winning strategy in this game; namely if, whatever the strategy β chooses in order to select the points x_n and the open sets V_n, α has a strategy for pick the open sets V_n that eventually results in a win for α.

Now α has a very simple winning strategy: do nothing, and just play the current open set V_n chosen by β for U_n. All the open sets U_n and V_n played during the game are non-empty, and therefore will all contain the root ε of S₀. Hence ε will be in ∩_{n ∈ N} U_n, and α will win.

In fact, it should be pretty obvious that every strategy for α is a winning strategy. This is a general fact on any topological space that has a largest element in its specialization preordering.

Every closed subspace of S₀ is Choquet-complete, and complete Baireness

The following is slightly less obvious: the winning strategy will require α to play one step, after which α will win whatever it does in subsequent rounds.

Proposition. Every closed subset C of S₀ is Choquet-complete in its subspace topology.

Proof. Initially, β picks a point x₀ in C, and an open neighborhood V₀ of x₀ in C. There is exactly one point s above x₀ in Max C. Let n be the length of s (as a sequence of numbers). Let T be the canonical tree representative of C, T_n be its truncation at depth n, namely the set of all sequences of length at most n in T. Then let E_n be the set of minimal elements of T_n. Since T is finitely branching, E_n is finite. Notice also that s is one of the elements of E_n. Then ↓(E_n–{s}) is a closed subset of S₀, which does not contain s. It does not contain x₀ either: otherwise x₀ would have a suffix in E_n–{s}, but since E_n is an antichain, that suffix would have to be incomparable with s, which is impossible since all the suffixes of a given sequence are pairwise comparable.

We let α play U₀ ≝ V₀ –↓(E_n–{s}). This is open in C, included in V₀, and contains x₀, as we have just argued, so it is legal for α to play it. Also, since s is not in ↓(E_n–{s}), and since V₀ is upwards-closed in C, s is in U₀. We claim that s is the unique largest element of U₀. Indeed, for every element t of U₀, t is below some element of E_n, by construction of E_n. Since t is not in ↓(E_n–{s}), that element cannot be in E_n–{s}, hence must be equal to s.

In subsequent rounds, we let α do nothing, namely play U_n ≝ V_n, for each n≥1 (for example). And we are now done: whatever sets V_n player β plays in subsequent rounds, since V_n is upwards-closed and non-empty, it must contain some element in Max C; that element must be U₀, since the open sets played during the game can only decrease; and there is only one available, which is s. Hence, at the end of the game, ∩_{n ∈ N} U_n will contain s, and therefore be non-empty. ☐

A space is Baire if and only if the intersection of countably many dense open subsets is dense. Theorem 7.6.8 of the book states that every Choquet-complete space is Baire. A space is completely Baire if and only if all its closed subspaces are Baire. We have just shown that all the closed subspaces of S₀ are Choquet-complete, hence Baire, so we obtain the following result of M. de Brecht.

Proposition [1, Theorem 6.3]. S₀ is completely Baire.

S₀ is not convergence Choquet-complete

S₀ is Choquet-complete in such a trivial fashion that one may wonder whether it could be more. For example, is it convergence Choquet-complete? A space is convergence Choquet-complete if and only if α has a (necessarily winning) strategy such that, whatever β plays, at the end of the game ∩_{n ∈ N} U_n contains a point x, and the open sets U_n form an base of open neighborhoods of x.

In [4], we have defined a relaxation of this notion: a space is compactly Choquet-complete if and only if α has a (necessarily winning) strategy such that, whatever β plays, at the end of the game ∩_{n ∈ N} U_n is a non-empty compact saturated set Q, and the open sets U_n form an base of open neighborhoods of Q. (“non-empty” added, January 25th, 2023.) Clearly, every convergence Choquet-complete space is compactly Choquet-complete (Q is obtained as ↑x).

In fact, as we will see now, S₀ has none of those properties.

Proposition. S₀ is not compactly Choquet-complete, hence not convergence Choquet-complete either.

Proof. We will design a strategy for β such that the final value of the game ∩_{n ∈ N} U_n = ∩_{n ∈ N} V_n is a single, infinite branch of the tree S₀, whatever strategy α uses. This is not compact saturated in S₀, since every compact saturated set is well-founded.

Initially, β picks x₀≝ε. Player β also picks any open neighborhood of it for V₀, for example S₀–↓0, or the whole of S₀. The winning strategy for β will be designed so that, at turn n, the point x_n is a sequence of length n.

Let us see how we pick that point. We let α play an open set U_n, which contains β’s previous point x_n–1. By using the same trick as the one we used to prove the failure of local compactness, we claim that x_n–1 has a successor (hence, of length n, assuming that the length of x_n–1 is n–1) inside U_n. Here is how. Let C_n be the complement of U_n. Let T_n be the canonical tree representative ↑Max C_n of C_n. Since T_n is finitely branching, x_n–1 has a successor x_n that is not in T_n. In order to show that x_n is in U_n, we reason by contradiction, and we assume that x_n is in C_n. Then, one of its suffixes, say u, is in Max C_n (by Lemma A). Since x_n is not in T_n, but u is, u cannot be x_n itself. Hence u is a suffix of x_n–1 (possible x_n–1 itself), namely x_n–1≤u. Since u is in Max C_n, hence in C_n, this implies that x_n–1 is also in C_n. This is impossible since x_n–1 is in its complement U_n. We have reached a contradiction, and thereby we have completed our argument that x_n is in U_n.

Player β also needs to produce an open neighborhood V_n of x_n included in U_n. As we wish β to eventually remove all the points on branches other than the branch x₀, x₁, …, x_n–1, x_n, …, β will have to produce V_n by removing a big closed set from U_n. The closed subset we remove will be a (finite) union of sets of the form ↓s, for various points s. None of these points should be above x_n, in order for V_n to still contain x_n in the end. Ideally, we would like to remove all sets ↓s, where s ranges over the points (=sequences) of length at most n (except for those s that are suffixes of x_n, as I have just said). But that would consist of infinitely many such sets. Hence, instead, we just remove those of length at most n and whose elements are all at most n as well. Explicitly, let us write x_n as a sequence of n natural numbers k_n…k₁. We consider the finite set E_n of points s of the form:

• m k_n–1…k₁, where m ranges over {0, …, n}–{k_n};
• m k_n–2…k₁, where m ranges over {0, …, n}–{k_n–1};
• …
• m k₂k₁, where m ranges over {0, …, n}–{k₃};
• m k₁, where m ranges over {0, …, n}–{k₂};
• m, where m ranges over {0, …, n}–{k₁}.

And β produces V_n ≝ U_n – ↓E_n.

Now this is enough to show that the final value ∩_{n ∈ N} U_n = ∩_{n ∈ N} V_n of the game is the infinite branch x₀, x₁, …, x_n–1, x_n, … ☐

By Proposition 9.1 of [4], every LCS-complete space is compactly Choquet-complete. (No, I will not prove this here!) An LCS-complete space is a space (homeomorphic to) a G_δ subset of a locally compact sober space. Let me state it explicitly as follows.

Proposition. S₀ is not LCS-complete.

Given that S₀ is sober, this is a much stronger result than our previous result that S₀ is not locally compact: S₀ cannot even occur as a G_δ subset of a locally compact sober space.

Since every quasi-Polish space is LCS-complete, we also obtain the following, which is due to M. de Brecht (in [1], obtained as an easy consequence of Theorem 5.6 there).

Proposition. S₀ is not quasi-Polish.

That S₀ is not LCS-complete is however not a strictly stronger result than saying that it is not quasi-Polish: by Theorem 9.5 of [4] (which I will not prove here either!), for a countably-based T₀ space such as S₀, it is equivalent to be LCS-complete, quasi-Polish, compactly Choquet-complete, or convergence Choquet-complete.

Conclusion

Let me sum up. S₀ is:

• sober;
• Choquet-complete, and all its closed subsets are Choquet-complete;
• completely Baire;
• countable and countably-based;
• not locally compact, not convergence Choquet-complete, not compactly Choquet-complete, hence not LCS-complete and not quasi-Polish.

All of those results (except the parts on Choquet-completeness) are due to M. de Brecht [1] (that paper contains much more!). I have only taken an angle on those results that go through the study of the strong Choquet game, in a way that I think is pleasing. Also, I have given explicit characterizations of the closed sets and the compact saturated subsets of S₀ in terms of subtrees, either finitely branching or well-founded, which I find useful — those, too, were well-known to M. de Brecht when we first discussed these matters.

I will leave the status of the consonance of S₀ to another time!

1. Matthew de Brecht. A generalization of a theorem of Hurewicz for quasi-Polish spaces. Logical Methods in Computer Science, 14(1:13)2018, pages 1–18, 2018; arXiv report 1711.09326.
2. Matthew de Brecht.  A note on the spatiality of localic products of countably based spaces. Computability, Continuity, Constructivity – from Logic to Algorithms (CCC 2019), 2019.
3. Andrea Schalk.  Algebras for Generalized Power Constructions. PhD Thesis, TU Darmstadt, 1993.
4. Matthew de Brecht, Jean Goubault-Larrecq, Xiaodong Jia, and Zhenchao Lyu. Domain-complete and LCS-complete Spaces. In Proceedings of the International Symposium on Domain Theory (ISDT’19), volume 345 of Electronic Notes in Theoretical Computer Science, pages 3–35, Yangzhou, China, June 2019. Elsevier Science Publishers.doi:10.1016/j.entcs.2019.07.014.

— Jean Goubault-Larrecq (January 21st, 2023)