In 1987, Gerhard Gierz produced another example of a compact semilattice without small semilattices [1]. It is a bit simpler than Jimmie Lawson’s counterexample, and it has an additional feature: it embeds into the Hilbert cube [0, 1]N, the product of a countably infinite number of copies of [0, 1], with its usual Hausdorff topology (although we will not say why here).
The fact that Gierz’s counterexample embeds into the Hilbert cube may seem paradoxical, as Lawson’s theorem (see Theorem D there) states that any compact semilattice that embeds into a power [0, 1]A, for any set A, must have small semilattices, right? Of course, there is a subtle point: any compact semilattice that embeds into [0, 1]A as a topological semilattice will have small semilattices. But Gierz’s counterexample will only embed as a topological space. That is, the embedding will be a topological embedding, but it will not map sums to sums.
In any case, let us proceed to the example. This is built in four steps.
Step 1: The compact semilattice ([0, 1]N, ⊓) and the functions fn and f : [0, 1]N → [0, 1]
We start from the Hilbert cube [0, 1]N itself, and we equip with the ⊓ operation (pointwise min). Gierz uses the pointwise max operation instead. Using mins will make step 2 slightly more complicated, but using maxes would force us to adjust our minds constantly later on, forcing us to juggle with min operations which are really maxes, or to deal with 1 being a zero and 0 being a one.
By Lawson’s theorem (see Theorem D there), ([0, 1]N, ⊓) is a compact lattice with small semilattices. We use the notation x (in boldface font, for lack of an overhang arrow) to denote elements of [0, 1]N, that is, sequences of elements of [0, 1]. For each such sequence x, we will write xn (no boldface, but a subscript) to denote its element at position n.
For every number n≥1, we define a function fn : [0, 1]N → [0, 1], by:
fn(x) ≝ 1 – log (1+n–x0–…–xn–1)/log (1+n),
where log is natural logarithm. In order to fix ideas, fn(x) is equal to gn(xn), where xn is the average of the first n entries of the tuple x, and gn is the function mapping t ∈ [0, 1] to 1–log(1+n–nt)/log(1+n) (also in [0, 1]); those functions gn are depicted in the graph below, for n=1, 2, 3, 4, 5, 6, 10, 20, 100 from top to bottom.
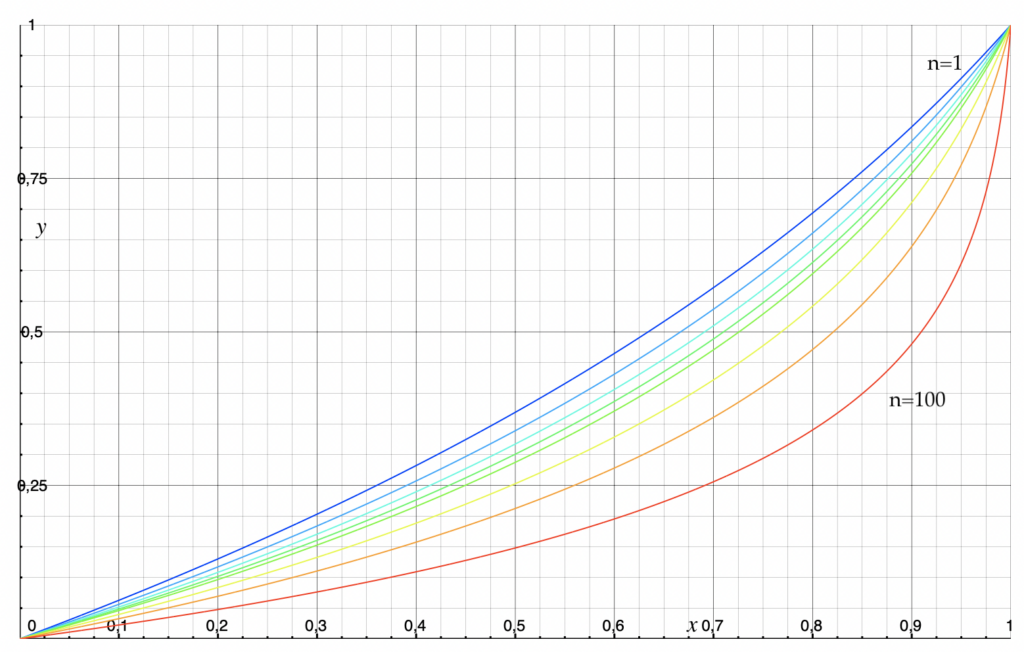
The functions fn are continuous, and monotonic with respect to the pointwise ordering on [0, 1]N; if you prefer, they are perfect maps from ([0, 1]σ)N to [0, 1]σ. They map any sequence that starts with n zeroes to 0, and any sequence that starts with n ones to 1.
Lawson’s counterexample also used some funny trickery with logarithms (see Fact (i) there, where we need to observe that for k large enough, log2log2 (1+k) + ε > log2 log2 (1+2k)). Here we need to observe that fn is almost a semilattice homomorphism, and looks more and more like one as n tends to infinity. In other words, the following inequalities hold.
Fact A. min (fn(x), fn(y)) – log 2/log (n+1) ≤ fn(x ⊓ y) ≤ min (fn(x), fn(y)),
for all x, y in [0, 1]N.
Proof. The second inequality fn(x ⊓ y) ≤ min (fn(x), fn(y)) is because fn is monotonic in its argument (not in n, mind you). The first inequality is more interesting. The proof below is unfortunately slightly more complex than Gierz’s, because of our choice of staying with pointwise mins: Gierz uses maxes instead, and his definition of fn is slightly simpler as a consequence.
Without loss of generality, we may assume that x0+…+xn–1 ≤ y0+…+yn–1, so fn(x) ≤ fn(y), and we need to show that fn(x) – log 2/log (n+1) ≤ fn(x ⊓ y). Let z ≝ x ⊓ y, so that zk = min (xk, yk) for every index k.
- We use the fact that, for any two numbers a and b in [0, 1], max(a, b) ≤ a+b.
- Hence also 1–min(a, b) = max(1–a, 1–b) ≤ (1–a)+(1–b).
- It follows that 1+n–z0–…–zn–1 = 1+(1–z0)+…+(1–zn–1) ≤ 1+(1–x0)+(1–y0)+…+(1–xn–1)+(1–yn–1).
- Remembering that x0+…+xn–1 ≤ y0+…+yn–1, this entails that 1+n–z0–…–zn–1 ≤ 1+2(1–x0)+…+2(1–xn–1), and the latter is less than or equal to 2+2(1–x0)+…+2(1–xn–1) = 2(1+n–x0–…–xn–1).
- Therefore log (1+n–z0–…–zn–1) ≤ log 2 + log (1+n–x0–…–xn–1), so log (1+n–z0–…–zn–1)/log (1+n) ≤ log 2/log (1+n) + log (1+n–x0–…–xn–1)/log (1+n), from which the desired inequality follows. ☐
Now we define:
f(x) ≝ infn≥1 fn(x).
At this point, we might think that Fact A would imply that f is a semilattice homomorphism, but that would be wrong. The wrong (but natural) proof consists in taking the infima on all terms of the inequalities in Fact A. Then infn ∈ N (min (fn(x), fn(y)) – log 2/log (n+1)) ≤ infn ∈ N fn(x ⊓ y) = f(x ⊓ y) ≤ infn ∈ N min (fn(x), fn(y)), and since log 2/log (n+1) tends to 0 as n tends to infinity, and since infs and mins commute, the leftmost term and the rightmost term would both be equal to f(x ⊓ y). There is some truth in that argument: infs and mins commute, so the rightmost term infn ∈ N min (fn(x), fn(y)) is indeed equal to min (f(x), f(y)), but the mistake lies in believing that infn ∈ N (min (fn(x), fn(y)) – log 2/log (n+1)) would be equal to infn ∈ N (min (fn(x), fn(y)): yes, infs behave like limits… but only for monotonic or antitonic sequences, and fn(x), fn(y), or their min, is not monotonic or antitonic in general.
Fact B. For all x, y in [0, 1]N, f(x ⊓ y) ≤ min (f(x), f(y)) but equality fails in general.
Proof. We have just shown f(x ⊓ y) ≤ min (f(x), f(y)); alternatively, this follows from the fact that f is a pointwise inf of monotonic functions, hence is itself monotonic. We now exhibit an example of two elements x, y in [0, 1]N such that f(x ⊓ y) < min (f(x), f(y)). Let a be any number such that 0<a<1; while the argument can be made to work for any such a, we will actually fix a to 1/2 later on. Let:
- x be (a, 1, 1, …) , starting with a, and then all the other entries are equal to 1;
- y be (1, a, 1, 1, …): a one, an a, and then only ones.
For every m≥1, fm(x) = 1–log(1+m–a–(m–1))/log(1+m) = 1–log(2–a)/log(1+m); this grows as m grows, so the least value of that when m varies with m≥1 is obtained with m=1, hence f(x)=1–log(2–a)/log 2.
For every m≥2 (not m≥1), fm(y) = 1–log(1+m–1–a–(m–2))/log(1+m) = 1–log(2–a)/log(1+m), and when m=1, we have fm(y) = 1–log(1+m–1)/log(1+m) = 1. Hence, as m enumerates the natural numbers starting from 1, the values of fm(y) start at 1, then drop to f2(y) = 1–log(2–a)/log 3, and then increase all the way to their limit, which is 1. The least of all those values, which is f(y) by definition, is therefore equal to 1–log(2–a)/log 3.
Now log 3>log 2>0, so log(2–a)/log 2 > log(2-a)/log 3, so f(x)=1–log(2–a)/log 2 is strictly smaller than f(y)=1–log(2–a)/log 3. Hence min (f(x), f(y)) = f(x) = 1–log(2–a)/log 2.
The infimum x ⊓ y is (a, a, 1, 1, …). For every m≥2, fm(x ⊓ y) = 1–log(1+m–a–a–(m–2))/log(1+m) = 1–log(3–2a)/log(1+m), and this grows as m grows; while for m=1, fm(x ⊓ y) = 1–log(1+m–a)/log(1+m) = 1–log(2–a)/log 2.
Plotting 1–log(2–a)/log 2 and 1–log(3–2a)/log 3 as functions of a in ]0, 1[ should convince you that 1–log(2–a)/log 2 > 1–log(3–2a)/log 3 for each such a. But we only need a counterexample, and for that we choose, say, a ≝ 1/2. Then 1–log(2–a)/log 2 ≈ 0.415037, while 1–log(3–2a)/log 3 ≈ 0.36907, so 1–log(2–a)/log 2 > 1–log(3–2a)/log 3 — for a=1/2.
With that value of a, then fm(x ⊓ y) starts out at 1–log(2–a)/log 2 ≈ 0.415037, then decreases to 1–log(3–2a)/log 3 ≈ 0.36907, and then goes up, tending to 1 as m tends to infinity. Taking the least of those values leads to the fact that f(x ⊓ y) = 1–log(3–2a)/log 3. But this is strictly less than 1–log(2–a)/log 2, which we had shown was the value of min (f(x), f(y)). ☐
So f is a not a semilattice homomorphism. It is not continuous either. Here is a counterexample. By the way, the elements un and 1 introduced below will be used again later.
Fact C. The function f is not continuous from [0, 1]N to [0, 1] (with their Hausdorff topologies). Explicitly, let:
- un ≝ (1, …, 1, 0, 0, …), with n ones at the beginning, and then only zeroes;
- 1 be the constant 1 sequence.
Then un tends to 1 in [0, 1]N as n tends to infinity, but f(un)=0 for every n ∈ N, and f(1)=1.
Proof. For every m>n, fm(un) = 1 – log (1+m–n)/log(1+m), which tends to 0 as m tends to infinity, so f(un)=0. For every m≥1, fm(1) = 1 – log(1+m–m)/log(1+m) = 1, so f(1)=1. ☐
However, f and the functions fn have the following property, which will be crucial in Step 3 below, and follows from Fact A.
Fact D. For all a<b in [0, 1], there is a number n0≥1 such that for all x, y ∈ [0, 1]N such that b ≤ min (f(x), f(y)), then a < fn(x ⊓ y) for every n≥n0.
Proof. Let us pick n0 so large that log 2/log (n0+1)<b–a. Let us assume that b ≤ min (f(x), f(y)). By Fact A, min (fn(x), fn(y)) – log 2/log (n+1) ≤ fn(x ⊓ y), so for every n≥n0, b ≤ min (f(x), f(y)) ≤ min (fn(x), fn(y)) < fn(x ⊓ y) + (b–a), hence a < fn(x ⊓ y). ☐
Step 2: The compact semilattice (S, +)
We build the space S of those pairs (x, r) in [0, 1]N × [0, 1] such that f(x)≥r.
As a set, S is the intersection of the sets Sn ≝ {(x, r) in [0, 1]N × [0, 1] | fn(x)≥r}, n≥1. Since fn is continuous and the graph of ≥ is closed in the product of [0, 1] with itself ([0, 1], with its Hausdorff topology and its usual ordering, is a compact pospace), Sn is closed in [0, 1]N × [0, 1] (in its Hausdorff topology). Therefore the intersection of all the sets Sn, which is S, is also closed. Being closed in a compact Hausdorff space, it is compact Hausdorff.
We define an operation + on S by:
(x, r) + (y, s) ≝ (x ⊓ y, min (r, s, f(x ⊓ y))).
Note that the right-hand side is in S. Indeed, f(x ⊓ y) ≥ min (r, s, f(x ⊓ y)).
Lemma E. (S, +) is a compact semilattice.
Proof. We know that S is compact Hausdorff. The + operation is commutative. We have (x, r) + (x, r) ≝ (x, min (r, r, f(x))) = (x, r) because f(x)≥r, by definition of S, so + is idempotent. Associativity is slightly tricker. We have ((x, r) + (y, s)) + (z, t) = (x ⊓ y, min (r, s, f(x ⊓ y))) + (z, t) = ((x ⊓ y) ⊓ z, min (min (r, s, f(x ⊓ y)), t, f((x ⊓ y) ⊓ z)))). We simplify the latter to (x ⊓ y ⊓ z, min (r, s, f(x ⊓ y), t, f(x ⊓ y ⊓ z)))). Since f is monotonic, f(x ⊓ y ⊓ z) ≤ f(x ⊓ y), so we can simplify even more to (x ⊓ y ⊓ z, min (r, s, t, f(x ⊓ y ⊓ z)))). We obtain the same formula for (x, r) + ((y, s) + (z, t)).
It remains to show that + is continuous. Since ⊓ is continuous, it suffices to show that the map g : ((x, r), (y, s)) ↦ min (r, s, f(x ⊓ y)) is continuous from S to [0, 1]. That may seem totally unlikely, since f is not continuous (Fact C), but Fact D will come to our rescue. As Gierz points out, this comes from Proposition VI-4.2 in the red book [2], but we will redo the proof by hand in order to understand what is happening here. We will show that g–1(]c, 1]) and g–1([0, c[) are both open, for every c ∈ [0, 1], and thus g will be continuous.
Claim: g–1(]c, 1]) is open. Let us first imagine that g ((x, r), (y, s)) > c, and let us find an open neighborhood W of ((x, r), (y, s)) which is mapped to ]c, 1] by g. We pick two numbers an and b such that c < a < b < g ((x, r), (y, s)). Using Fact D, we find n0≥1 such that for all u, v ∈ [0, 1]N such that b ≤ min (f(u), f(v)), then a < fn(u ⊓ v) for every n≥n0. We note that a < fn(x ⊓ y) for every n≥1, since a < g ((x, r), (y, s)) = min (r, s, f(x ⊓ y)) ≤ f(x ⊓ y) < fn(x ⊓ y). Since ⊓ and fn are continuous, there is an open rectangle Un × Vn containing (x, y) and mapped by fn(_ ⊓ _) to ]a, 1].
The desired open neighborhood W is the product of (∩n=1n0 Un × ]b, 1]) ∩ S with (∩n=1n0 Vn × ]b, 1]) ∩ S. Note that this open because we are taking finite intersections of open sets Un, resp. Vn. Let us check that ((x, r), (y, s)) belongs to W and that W is mapped to ]a, 1] by g:
- ((x, r), (y, s)) is in U: indeed, g ((x, r), (y, s)) = min (r, s, f(x ⊓ y)) > b, so r, s > b; and x is in every Un (even not just for n<n0), and y is in every Vn, by construction.
- For every pair ((u, r’), (v, s’)) in U, we have r’, s’ > b and also u ∈ Un and v ∈ Vn for every n with 1≤n<n0, by definition of U. Hence fn(u ⊓ v) > a for every n with 1≤n<n0. The same inequality holds for every n≥n0 because of our choice of n0, using Fact D. Takings infima over all n≥1, we obtain that f(u ⊓ v) ≥ a > c. We have r’, s’ > b > a > c, so g ((u, r’), (v, s’)) = min (r’, s’, f(u ⊓ v)) > c.
Claim: g–1([0, c[) is open. Next, let us imagine that g ((x, r), (y, s)) < c, and let us find an open neighborhood W of ((x, r), (y, s)) which is mapped to [0, c[ by g. This is much easier. Since g ((x, r), (y, s)) = min (r, s, f(x ⊓ y)) < c, we have r<c or s<c or f(x ⊓ y) < c. If r<c, then the product of ([0, 1]N × ]c, 1]) ∩ S by S is an open neighborhood of ((x, r), (y, s)) that is mapped by g to [0, c[. If s<c, then we choose the product of S by ([0, 1]N × ]c, 1]) ∩ S for W instead. Finally, if f(x ⊓ y) < c, then there is a number n≥1 such that fn(x ⊓ y) < c. (Beware: the sequence fn is not monotonic or antitonic in general, so that does not imply that a similar inequality would hold for every larger n as well. But this will not matter.) Since ⊓ and fn are continuous, there is an open rectangle Un × Vn containing (x, y) and mapped by fn(_ ⊓ _) to [0, c[. We then define W as the product of (Un × [0, 1]) ∩ S with (Vn × [0, 1]) ∩ S. This is an open neighborhood of ((x, r), (y, s)), and for every pair ((u, r’), (v, s’)) in W, we have fn(u ⊓ v) < c, hence f(u ⊓ v) < c, by definition of f as an inf, and therefore g ((u, r’), (v, s’)) = min (r’, s’, f(u ⊓ v)) < c. ☐
Step 3: A funny thing happens to interval homomorphisms on (S, +)
Some strange things start to occur with the following observation. Let us recall that I is the compact semilattice ([0, 1], min) (and it has small semilattices). Let 1 be the constant 1 sequence. We have f(1)=1, so (1, r) is in S for every r ∈ [0, 1].
Proposition F. For every continuous semilattice homomorphism φ from S to I, φ(1, 0) = φ(1, 1).
Proof. As with every semilattice, the operation + induces an ordering on S, defined by (x, r) ⊑ (y, s) if and only if (x, r) = (x, r) + (y, s), for which + is binary infimum, and then any semilattice homomorphism preserves infima, hence is monotonic. Now if r≤s (and r, s ≤ f(x)), then (x, r) + (x, s) = (x, min (r, s, f(x))) = (x, r), so (x, r) ⊑ (x, s), and therefore φ(x, r) ≤ φ(x, s). (Oh yes, the ordering associated with the min operation on I is the usual ordering ≤.) In particular, φ(1, 0) ≤ φ(1, 1).
For the sake of contradiction, let us assume that φ(1, 0) < φ(1, 1). Let a be any real number such that φ(1, 0) < a < φ(1, 1). Then (1, 1) is in the open set φ–1(]a, 1]), and (1, 0) is in the open set φ–1([0, a[),. We will build several sequences of elements of S; some will tend to (1, 0), some others will tend to (1, 1).
- Our first sequence of elements xn is built as follows. Let en be the element (1, …, 1, 0, 1, …) in [0, 1]N, with its unique 0 at position n. For every natural number m, fm(en) = 1 – log (1+m–m)/log (1+m) = 1 if m≤n and fm(en) = 1 – log (1+m–m+1)/log (1+m) = 1 – log 2/log (1+m) if m>n, and taking infima over all m≥1 yields that f(en) = 1 – log 2/log (2+n). Hence (en, 1 – log 2/log (2+n)) is in S for every natural number n. We let xn ≝ (en, 1 – log 2/log (2+n)).
- As n tends to infinity, xn tends to (1, 1), so φ(xn) > a for n large enough. In other words, there is a natural number n0 such that φ(xn) > a for every n≥n0.
- Let us fix some n≥n0 (here and in the next item), and let us look at xn+…+xn+k, for any natural number k. Since φ is a semilattice homomorphism, it maps sums to mins, so φ(xn+…+xn+k) = min (φ(xn), …, φ(xn+k)) > a, where the latter inequality is because n, n+1, …, n+k are all larger than or equal to n0, and using the previous item.
- Explicitly, xn+…+xn+k = (en ⊓ … ⊓ en+k, rnk), where rnk is a min of various values. As k tends to infinity, en ⊓ … ⊓ en+k tends to the sequence un ≝ (1, …, 1, 0, 0, …), with n ones at the beginning, and then only zeroes. Therefore xn+…+xn+k tends to (un, rn) for some value rn≤f(un). Since f is continuous, f(en ⊓ … ⊓ en+k) tends to f(un) as k tends to infinity. But, for every m>n, fm(un) = 1 – log (1+m–n)/log(1+m), which tends to 0 as m tends to infinity, so f(un)=0, and hence, rn=0. To sum up, we have obtained that, as k tends to infinity, xn+…+xn+k tends to (un, 0). Since φ(xn+…+xn+k) > a for every k, as we have seen in the previous item, we have φ(un, 0) ≥ a.
- However, as n tends to infinity, (un, 0) tends to (1, 0), so φ(un, 0) < a for n large enough (remember that (1, 0) is in the open set φ–1([0, a[)), which is impossible. ☐
We arrive at the fourth and final step. Proposition F is the key, and it remains to build an appropriate quotient of S, which will turn the funny result of Proposition F into something much more radical.
Step 4: The Rees quotient (S/≡, +)
We define an equivalence relation ≡ on S by declaring that (x, r) ≡ (y, s) if and only if either (x, r) = (y, s) or r=s=0 (and x and y are arbitrary). We build the quotient S/≡, with the quotient topology. Since S/≡ is the image of a compact space by the quotient map, which is continuous, S/≡ is compact.
We wish to show that S/≡ is Hausdorff, and that addition + on S induces a continuous semilattice operation on S/≡, by passing to equivalence classes. To this end, we note that S/≡ is what it known as the Rees quotient of the semigroup (S, +) by an ideal. (A semigroup is a set with an associative operation + on it, and we will define ideals below.) Explicitly, ≡ has only one non-trivial equivalence class: the equivalence class [0, 1]N × {0} of any point of the form (x, 0); the equivalence class of any point (x, r) with r≠0 consists just of (x, r), and is therefore trivial. The non-trivial equivalence class [0, 1]N × {0} is an ideal, meaning that the sum of any element (x, 0) of [0, 1]N × {0} with any other element (y, s) is in [0, 1]N × {0}: in other words,(x, 0)+(y, s)=(x ⊓ y, 0). Conversely, given any semigroup G and any ideal J of G, we may define an equivalence relation ≈ on G by u≈v if and only if u=v or both u and v are in J. The quotient G/≈, usually written as G/J, is the Rees quotient of G by J, by definition.
Lemma G. Let (G, +) be a semigroup, and J be an ideal of G. Let q : G → G/J be the quotient map. Then (G/J, +) is a semigroup where + is defined on G/J by q(u)+q(v) ≝ q(u+v).
If G is a semilattice, then so is G/J.
If G is a compact semigroup (namely if G is topologized in such a way that it is compact Hausdorff and + is jointly continuous) and J is closed in G, then G/J is a compact semigroup (with the quotient topology).
Proof. We first show that + is well-defined, namely that the definition of q(u)+q(v) does not depend on u (or v) in its equivalence class. This boils down to the verification that if u≈u’ then u+v≈u’+v. If u=u’, this is clear. Otherwise, u and u’ are both in J, and therefore u+v and u’+v are both in J as well, since J is an ideal; therefore u+v≈u’+v.
It is then clear that + is associative, commutative if + is commutative, and idempotent if + is idempotent. Then G/J is a semilattice if G is.
Let us now assume that G is a compact semigroup, and that J is closed in G. Note that G is compact Hausdorff, so J is in fact compact as well. G/J is the image of the compact space G by the continuous map q, hence is compact. We claim that G/J is Hausdorff. Let us consider any two distinct points q(u), q(v) in G/J.
- If both u and v are outside J, then there is an open neighborhood U of u and an open neighborhood V of v in G that are disjoint. We can assume that neither U nor V intersects J, replacing them by U–J and V–J if necessary, respectively. This is possible because J is closed. Then U and V are ≈-saturated: given any element in U (resp. V), any element ≈-equivalent to it must also be in U (resp. V). Hence their images q[U] and q[V] by the quotient map q are open (see Proposition 4.10.20 in the book). Additionally, q[U] contains q(u), q[V] contains q(v), and they are disjoint, because q is injective outside J.
- If u is in J but v is not, then we use the fact that G, being compact Hausdorff, is T4 (Proposition 4.4.17 in the book) hence T3 (comment after Definition 4.1.22 in the book), so there is an open neighborhood U of J (not just of u) that is disjoint from some open neighborhood of v. Since U contains J, U is ≈-saturated, and V is ≈-saturated because it is disjoint from J. Hence q[U] and q[V] are open, and they must be disjoint.
- The case where u is not in J and v is is symmetric.
We finally wish to show that + is continuous, at any pair of points q(u), q(v). To this end, we consider any open neighborhood W of q(u)+q(v). Since + is (jointly) continuous and since q is continuous, there is an open neighborhood U of u and there is an open neighborhood V of v in G such that U × V ⊆ +–1(q–1(W)).
- If both u and v are outside J, then we can assume that neither U nor V intersects J, replacing them by U–J and V–J if necessary, as in the proof that G/J is Hausdorff. Then U and V are ≈-saturated, so q[U] and q[V] are open, and then q[U] × q[V] is an open neighborhood of the pair (q(u), q(v)) whose image under + is included in W.
- If u is in J, then we reason as follows. The sum u+v is in J, since J is an ideal. Therefore W contains q(u+v)=q[J], so J ⊆ q–1(W), and hence J × G ⊆ +–1(q–1(W)) (every sum of an element of J with an element of G is in J, since J is an ideal). An easy theorem due to Alexander Doniphan Wallace [3, Chapter II, Theorem 12] states that any product K1 × K2 of compact sets included in an open set W is included in a basic open set U × V included in W. (See the Appendix for a proof.) Here J is compact, being closed in the compact space G. Hence there is an open neighborhood U, not just of u, but in fact of the whole of J, and an open neighborhood V of G (yes, that must be G itself) such that U × V ⊆ +–1(q–1(W)). Since U contains J, U is ≈-saturated. V=G is also ≈-saturated. Then q[U] × q[V] is an open neighborhood of the pair (q(u), q(v)) and its image under + is included in W.
- The case is similar if v is in J. ☐
As a consequence of Lemma G (with Lemma E, saying that (S, +) is a compact semilattice, and using the fact that J ≝ [0, 1]N × {0} is clearly closed in S), (S/≡, +) is a compact semilattice.
Now let us assume a continuous semilattice homomorphism ψ from S/≡ to I. Then φ ≝ ψ o q (where q is the quotient map) is continuous, and is a semilattice homomorphism: φ(u+v) = ψ(q(u+v))=ψ(q(u)+q(v))=min(ψ(q(u)), ψ(q(v)))=min(φ(u), φ(v)). We have the following.
- In a Rees quotient, the unique non-trivial equivalence class J is a zero (an absorbing element): adding it to anything gives you back zero. Explicitly, if u is in J, then u+v is in J for every element v, so q(u)+q(v) = q(u) = q[J]; equivalently, q[J] = q[J]+v. In the case of S/≡, J = [0, 1]N × {0}, and taking u ≝ (1, 0), we obtain that φ(1, 0) = ψ(q(1, 0)) = ψ(q[J]). Since ψ is a semilattice homomorphism, ψ(q[J]) = ψ(q[J]+q(v)) = min (ψ(q[J]), ψ(q(v))) for every v in S, so φ(1, 0) = min (φ(1, 0), φ(v)). In other words, φ(1, 0) ≤ φ(v), for every v in S.
- The element (1, 1) is a unit: adding it to any v gives you back v. Indeed, for every (y, s) in S, (1, 1)+(y, s) = (1 ⊓ y, min (1, s, f(1 ⊓ y))) = (y, min (1, s, f(y))) = (y, s), using the fact that s≤f(y), by definition of S. Since φ is a semilattice homomorphism, min (φ(1, 1), φ(v)) = φ((1, 1) + v) = φ(v). Namely, φ(v) ≤ φ(1, 1), and this for every v in S.
- By Proposition F, φ(1, 0) = φ(1, 1). It follows from the previous two items that φ(v) = φ(1, 0) = φ(1, 1) for every v in S. Hence φ is constant, and therefore so is ψ.
In particular, (S/≡, +) certainly does not have enough interval homomorphisms. Its only interval homomorphisms are constant, and cannot separate any pair of points. By Theorem D, we conclude:
Theorem (Gierz). (S/≡, +) is a compact semilattice that does not have small semilattices. More precisely, all its interval homomorphisms are constant.
Conclusion
Additionally, Gierz shows that S/≡ is homeomorphic to the Hilbert cube [0, 1]N. We will skip that part. This involves, first, showing that S is homeomorphic to an infinite dimensional convex subset of the Hilbert cube. That is not hard. By a theorem due to O. H. Keller, S is then homeomorphic to the Hilbert cube itself, and then the homeomorphism equates the non-trivial equivalence class J = [0, 1]N × {0} with a face of the Hilbert cube, from which it follows that S/≡ is itself homeomorphic to the Hilbert cube. That would require us to explain many more things here, and we will simply not do so.
- Gerhard Gierz. A compact semilattice on the Hilbert cube with no interval homomorphism. Proceedings of the American Mathematical Society 101(4):592–594, 1987.
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- John Leroy Kelley. General Topology. University Series in Higher Mathematics. Princeton, New Jersey, Toronto, New York London: D. Van Nostrand company, 1955.
— Jean Goubault-Larrecq and Zhenchao Lyu (November 20th, 2023)

Goubault-Larrecq
Appendix A: Wallace’s theorem
Fact (Wallace’s theorem). Given two compact subsets K1, K2 of a topological space X, and an open neighborhood W of K1 × K2 in X × X (with the product topology), there is an open rectangle U × V included in W that contains K1 × K2.
Proof. We start by fixing x ∈ K1. For every y ∈ K2, there is an open rectangle Uxy × Vxy containing (x, y) and included in W. In particular, the sets Vxy cover K2 as y varies over K2. Since K2 is compact, there is a finite subset E of K2 such that K2 ⊆ ∪y∈E Vxy. We let Ux ≝ ∩y∈E Uxy. This is an open neighborhood of x, since E is finite. We let Vx ≝ ∪y∈E Vxy. Every point of Ux × Vx is in Ux × Vxy for some y ∈ E, hence in Uxy × Vxy, hence in W. We have show that Ux × Vx is included in W.
The sets Ux form an open cover of K1 as x varies over K1. Hence there is a finite subset E of K1 such that K1 ⊆ ∪x∈E Ux. Let U ≝ ∪x∈E Ux and V ≝ ∩x∈E Vx, and let us note that V is open, since E is finite. Since every Vx contains K2, V contains K2, and therefore U × V contains K1 × K2. Finally, U × V is a union of sets Ux × V, each one is included in Ux × Vx, which is included in W, as we have seen in the previous paragraph. Therefore U × V is included in W, too. ☐
