We have already talked about compact semilattices here (and we will give back the definition below). A puzzling property was that one needs them to have small semilattices in a number of applications. For example, the fundamental theorem of compact semilattices says that there is a tight connection between compact semilattices with small semilattices and bc-domains (more on this below). Most compact semilattices seem to have small semilattices, so it was a natural question whether there existed compact semilattices without small semilattices at all. This question was answered in the positive by Jimmie Lawson in 1970 [1], and we have described his counterexample here, although under a slightly different angle.
The purpose of today’s post is to show that there are a lot of other compact semilattices without small semilattices. Although we had eluded this (pretty fundamental) fact in the previous posts on compact semilattices, we will state another characterization of the ‘small semilattice’ property: a compact semilattice has small semilattices if and only if it has enough of something called interval homomorphisms (namely, enough continuous semilattice homomorphisms to ([0, 1], min) to separate the points, see later), or equivalently it embeds, both as a topological space and as a semilattice, into a product of copies of [0, 1], with pointwise min as addition.
This gives a practical way of showing that a given compact semilattice does not have small semilattices: it suffices to show that it does not have enough interval homomorphisms. This was how Lawson’s counterexample was originally proved to not have small semilattices: it does not have enough interval homomorphisms, in the worst possible way, as all its interval homomorphisms are constant, and none can therefore separate any pair of distinct points.
We will see, by a simple argument, that any product of a compact semilattice without small semilattices (e.g., Lawson’s) with any compact semilattice must also fail to have small semilattices. This will give us quite a lot of compact semilattices without small semilattices.
Then we will see that the Hoare hyperspace of any compact semilattice (L, +) (with its upward topology) is again a compact semilattice, and that if (L, +) does not have small semilattices, then this Hoare hyperspace will not have small semilattices either, giving us even more examples of compact semilattices without small semilattices. This part will require us to use a flurry of results. Most of them have been presented on this blog, but not all of them; apologies for that!
Compact semilattices, bc-domains
A semilattice is a pair (L, +) where L is a set and + is an associative, commutative, and idempotent operator +. It is topological if + is (jointly) continuous. In this previous post, we talked about the fundamental theorem of compact semilattices: there is an isomorphism of categories between:
- CSLattSmall, the category of compact semilattices (short for compact Hausdorff topological semilattices) with small semilattices, with continuous semilattice homomorphisms as morphisms, and
- Bcd/inf, the category of bc-domains and non-empty-inf-preserving Scott-continuous maps.
The property of having small semilattices was introduced by Jimmie Lawson [2]. A topological semilattice (L, +) has small semilattices if and only if for every point x in L, every open neighborhood of x contains a neighborhood sub-semilattice A of x, namely a set A whose interior contains x, and which is closed under +.
The isomorphism of categories sends every compact semilattice (L, +) to the space L itself, ordered by x≤y if and only if x=x+y (this makes it a bc-domain); and conversely, it maps every bc-domain X to (Xλ, ⋀), where Xλ is X with the Lawson topology (or, equivalently, the patch topology—beware that the patch and Lawson topologies differ on general dcpos, but they agree on continuous dcpos), and ⋀ is the binary infimum operation.
A bc-domain indeed has binary infima, and in fact infima of all non-empty families. Moreover, the binary infimum operation ⋀ is jointly continuous. Indeed, it is Scott-continuous, hence separately continuous, and by Ershov’s observation, since every bc-domain is continuous, it must be continuous. Hence a bc-domain is automatically a topological semilattice as well.
Additionally, every bc-domain X is a topological semilattice with small semilattices. Indeed, being continuous, X has a base of its Scott topology consisting of open filtered subsets (Proposition 5.1.19 in the book), and a filtered subset is closed under ⋀, by definition.
Finally, a bc-domain is a deflationary topological semilattice (with small semilattices). This means that every sum of two elements x and y (namely, x ⋀ y in a bc-domain) is smaller than or equal to both x and y.
We have seen that the T0 deflationary topological semilattices with small semilattices are exactly the algebras of the Qfin monad in another, older post, a result due to Andrea Schalk [3]. And this is also where we have described Lawson’s counterexample [1], in the form of a T0 deflationary topological semilattice without small semilattices. This space is even stably compact, and a complete lattice under its specialization ordering.
Interval homomorphisms
A very simple example of a compact semilattice is ([0, 1], min), where [0, 1] is given its usual Hausdorff topology. It has small semilattices, simply because every open subset of [0, 1] is a semilattice with respect to the min operation. The fundamental theorem of compact semilattices predicts that [0, 1] should be a bc-domain when ordered by x≤y if and only if x=min(x,y): this is just the usual ordering on [0, 1], and indeed [0, 1] is a bc-domain, even a continuous complete lattice, under this ordering. The space [0, 1]σ obtained by giving it the Scott topology is a stably compact space (Fact 9.1.6 in the book), and its patch space is ([0, 1], ≤), by the general theory of compact pospaces (Section 9.1 in the book).
Jimmie Lawson proved that a compact semilattice (L, +) has small semilattices if and only if it has enough interval homomorphisms, by which we mean the following property: for every pair of distinct points x and y in L, there is a continuous semilattice homomorphism f from (L, +) to ([0, 1], min) (an interval homomorphism) such that f(x)≠f(y) [2, Theorem 4.3].
Let us give a proof of this. In one direction, if (L, +) is a compact semilattice with small semilattices, then L with the ordering ≤ defined by x≤y if and only if x=x+y is a bc-domain, as we have said above, and we use the following lemma. For every poset X, Xσ is X with its Scott topology.
Lemma A. Let X be a continuous dcpo, and x and y be two points such that x≪y. Then there is a Scott-continuous map f : X → [0, 1] such that f(z)=0 for every point z such that x is not way-below z, and f(y)=1. If Xσ is compact, then f is perfect from Xσ to [0, 1]σ. If X has binary infima (for example, if X is a bc-domain), then we can require f to map binary infima to binary infima, namely, f(u ⋀ v) = min (f(u), f(v)) for all u, v ∈ X.
Proof. We use a Urysohn-style construction. Explicitly, it suffices to use Proposition 6.3.17 in the book with the upward scale consisting of complements X–↑z of upward closures of points z (plus the empty set) and the downward scale consisting of the sets ↟z (plus the whole of X), but it will be clearer to do the construction by hand. In any case, the final part of the lemma, that f preserves binary infima, will have to be checked separately.
The idea of the construction is given in the picture shown on the right.
We define a family of points xa, where a ranges over the set I2 of dyadic numbers in [0, 1], as follows. First, we define x0 as x and x1 as y. Then, we pick a point x1/2 such that x0 ≪ x1/2 ≪ x1, using interpolation (Proposition 5.1.15 in the book); then a point x1/4 such that x0 ≪ x1/4 ≪ x1/2, and a point x3/4 such that x1/2 ≪ x3/4 ≪ x1, using interpolation again; and so on.
A bit more formally, assuming we have already defined xa for all numbers a that we can write as p/2n, 0≤p≤2n, we enumerate the numbers a≝p/2n, 0≤p≤2n–1, and letting b≝(p+1)/2n, we define xa+b as any element of X such that xa ≪ xa+b ≪ xb, using interpolation.
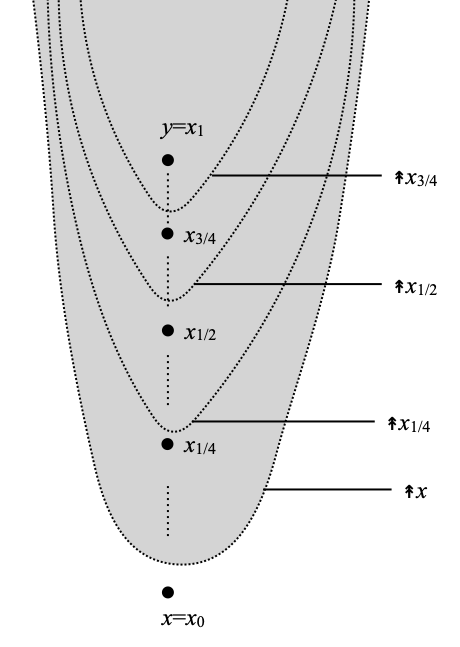
This allows us to make sense of xa for all numbers a that we can write as p/2n+1, 0≤p≤2n+1. By induction on n, we have defined a family of points xa, a ∈ I2, such that x0=x, x1=y, and such that a<b implies xa ≪ xb.
We define f(z) as sup {a ∈ I2 | xa ≪ z} for every z ∈ X (we take the supremum of the empty to be 0, so that f(z)=0 if x0=x is not way-below z). We also define g(z) as inf {b ∈ I2 | xb ≰ z} (where the infimum of the empty is 1, so that g(z)=1 if x1=y is less than or equal to z). Now:
- For every z ∈ X, f(z)≤g(z). It suffices to observe that if xa ≪ z and xb ≰ z, then a≤b. In fact, if a>b, we would have xb ≪ xa, hence xb ≪ z, hence xb ≤ z, which is impossible.
- For every z ∈ X, f(z)=g(z). Otherwise, the open interval ]f(z), g(z)[ would be non-empty, and therefore would contain an element of I2, and in fact infinitely many. Let us pick two elements c, d ∈ I2 in ]f(z), g(z)[ with c<d. Since f(z) < c, we have that xc cannot be way-below z. Since g(z)>d, we must have xd ≤ z. But c<d, so xc ≪ xd. From xc ≪ xd ≤ z, we deduce that xc is way-below z (see Proposition 5.1.4 in the book), and this is impossible. Therefore f(z)=g(z).
- f is Scott-continuous from X to [0, 1], namely, continuous from Xσ to [0, 1]σ. Indeed, for every t ∈ ]0, 1[, f–1(]t, 1]) is the union of the set ↟xa over all a ∈ I2 such that a>t, and the sets ↟xa are Scott-open (Proposition 5.1.17 in the book).
- f is perfect from Xσ to [0, 1]σ, provided that Xσ is compact. A perfect map is a continuous map such that the inverse image of a compact saturated subset is compact. We already know that f is continuous. Also, we have shown that f=g, so it suffices to show that g–1([t, 1]) is compact for every t ∈ [0, 1]. (The non-empty compact saturated subsets of [0, 1]σ are upwards-closed, hence they are intervals with 1 as right endpoint, and it is easy to see that they must contain their left endpoint, otherwise they would not be compact.) If t=0, then g–1([t, 1]) is the whole of X, which we have assumed to be compact. Hence we concentrate on the case t>0. We realize that g–1([t, 1]) is equal to {z ∈ X | for every b ∈ I2 such that xb ≰ z, b≥t} = {z ∈ X | for every b ∈ I2 such that b<t, xb ≤ z} = ↑supb ∈ I2, b<t xb, and this is compact saturated (and a very special compact saturated set, really). We note that supb ∈ I2, b<t xb exists because the collection of elements xb is a chain, in fact a non-empty chain since t>0, and because X is a dcpo.
- f(y)=1: because xa ≪ x1=y for every a ∈ I2 such that a<1, f(y) is larger than or equal to 1, and it cannot be more than 1, since the suprema defining f is over values in [0, 1].
- f(z)=0 for every point z such that x is not way-below z: if x0=x is not way-below z, then no xa is way-below z, otherwise x0 ≪ xa ≪ z (and ≪ is transitive, by Proposition 5.1.4 in the book for example); then f(z) is the supremum of the empty family, namely 0.
- Let us assume that X has binary infima. Since f is continuous, it is monotonic, so f(u ⋀ v) ≤ min (f(u), f(v)) for all points u and v of X. For the sake of contradiction, we assume that f(u ⋀ v) < min (f(u), f(v)). By symmetry, we may assume that f(u) ≤ f(v). Hence f(u ⋀ v) < f(u) ≤ f(v). Since f(u ⋀ v) < f(u), there is a dyadic number xc ∈ I2 such that f(u ⋀ v) < c < f(u).
Since f(u)>c, there is an a ∈ I2 such that a>c and xa ≪ u. Since f(v) ≥ f(u) > c, there is a b ∈ I2 such that b>c and xb ≪ v. Replacing a and b by the least of the two, we may assume that a=b. For example, if a<b, then we would replace xb by xa; since xa ≪ xb and xb ≪ v, we would have xa ≪ v, in addition to xa ≪ u. (The case b<a is symmetrical.) Hence we have a dyadic number a>c such that xa ≪ u and xa ≪ v. In particular, xa ≤ u and xa ≤ v. Therefore xa ≤ u ⋀ v.
Now we use the fact that f(u ⋀ v) < c. Since f=g, we have, equivalently, g(u ⋀ v) < c. By definition of g, there is dyadic number b ∈ I2 such that b<c and xb ≰ u ⋀ v.
We put everything together: we have b<c<a, so xb ≪ xa. With xa ≤ u ⋀ v, this gives us xb ≪ u ⋀ v, hence xb ≤ u ⋀ v (see Proposition 5.1.4 in the book), contradicting xb ≰ u ⋀ v. Therefore our initial assumption f(u ⋀ v) < min (f(u), f(v)) was wrong, and hence f(u ⋀ v) = min (f(u), f(v)). ☐
Corollary B. For every bc-domain X, for all points y and z of X such that y≰z, there is a perfect semilattice homomorphism f : (Xσ, ⋀) → ([0, 1]σ, min) such that f(y)=1 and f(z)=0.
Proof. The point y is the supremum of a directed family of points x way-below y, since every bc-domain is a continuous dcpo, by definition. If all of them were smaller than or equal to z, then y would be smaller than or equal to z. Hence there is a point x ≪ y such that x≰z. By Lemma A, and since every bc-domain is a continuous dcpo that is pointed, hence compact, there is a perfect map f : Xσ → [0, 1]σ such that f(z)=0 for every point z such that x is not way-below z (and in particular for our point z: if x were way-below z, then we would have x≤z), and f(y)=1. Also, f maps binary infima to mins, hence is a semilattice homomorphism. ☐
Corollary C. Let (L, +) be a compact semilattice with small semilattices. Then (L, +) has enough interval homomorphisms.
Proof. Let X be the bc-domain underlying L, namely: X has the same points as L, and is ordered by x≤y if and only if x=x+y, for all points x and y. Let y and z be two distinct points in L (equivalently, X). By symmetry, we may assume that y≰z. We take f as in Corollary B. Being perfect from Xσ to [0, 1]σ, which are stably compact spaces, f is continuous between their patch spaces, with are L and [0, 1] (with its usual Hausdorff topology) respectively. Since addition + in L is inf (⋀), f is a homomorphism from (L, +) to ([0, 1], min). We have f(y)=1 and f(z)=0, hence in particular f separates y from z. ☐
The collection of interval homomorphisms on L is traditionally written as Hom(L,I): this is the collection of continuous semilattice homomorphisms from (L, +) to I≝([0, 1], min). Now we can form a canonical compact semilattice IHom(L,I). This is easier done through bc-domains. We form the product ([0, 1]σ)Hom(L,I) of as many copies of [0, 1]σ as there are interval homomorphisms on L. This is a bc-domain, because any product of bc-domains is a bc-domain (exercice! do not forget that every bc-domain is pointed, so their product is continuous). We have already recalled that every bc-domain is stably compact, and its patch space is a compact semilattice with small semilattices. Since the patch space construction commutes with products (Proposition 9.3.1 in the book), the patch space of ([0, 1]σ)Hom(L,I) is simply [0, 1]Hom(L,I). Let us write the latter as IHom(L,I). Its semilattice operation, which we will write as ⊓, is the binary infimum operation for the specialization ordering of ([0, 1]σ)Hom(L,I), which is defined pointwise. In other words, and realizing that the elements φ, ψ of IHom(L,I) are simply the functions from Hom(L,I) to I, φ ⊓ ψ maps every interval homomorphism f on L to min (φ(f), ψ(f)).
The same argument shows that (IA, ⊓) is a compact semilattice with small semilattices, for any set A, and where ⊓ is pointwise min. The fact that we took A as Hom(L,I) in the previous paragraph did not play any rôle.
If (L, +) is a compact semilattice with enough interval homomorphisms, then we claim that it embeds into IHom(L,I) as a topological semilattice. Namely, there is a topological embedding j : L → IHom(L,I) that maps sums to mins. Indeed, we define j(x) as the map f ∈ Hom(L,I) ↦ f(x). The continuity of j is equivalent to the fact that πf o j is continuous for every f ∈ Hom(L,I), by definition of the product topology on IHom(L,I); πf is projection onto component f, hence (πf o j) (x) = j(x)(f) = f(x), so πf o j = f is indeed continuous. Since (L, +) has enough interval homomorphisms, j is injective: if x≠y, then f(x)≠f(y) for some f ∈ Hom(L,I), so j(x) and j(y) differ at component f. But every continuous injective map from a compact space to a Hausdorff space is a topological embedding (see Exercise 4.10.10 in the book), so j is a topological embedding. Finally, j(x+y)(f) = f(x+y) = min (f(x), f(y)) = min (j(x)(f), j(y)(f)) for all x, y in L, so j(x+y) = j(x) ⊓ j(y), showing that j is a topological semilattice embedding.
Now let us consider any topological semilattice (L’, +’) that embeds (as a topological semilattice) into (IA, ⊓), or more generally into any topological semilattice (L”, +”) with small semilattices. In other words, let us assume a topological embedding f from L’ to L” that is also a morphism of semilattices, namely that maps +’-sums to +”-sums. Then (L’, +’) must have small semilattices as well. Indeed, let x be any element of L’, and U be an open neighborhood of x in L’. Since f is a topological embedding, U must be equal to f–1(V) for some open subset V of L”. Additionally, f(x) is in V. Since (L”, +”) has small semilattices, f(x) is in the interior of some sub-semilattice B of (L”, +”) included in V. Then f–1(B) is a neighborhood of x, which is included in U=f–1(V), and is closed under +’ because f is a semilattice homomorphism and B is closed under ⊓.
We have therefore obtained Lawson’s theorem.
Theorem D. For a compact semilattice (L, +), the following are equivalent:
- (L, +) has small semilattices;
- (L, +) has enough interval homomorphisms;
- (L, +) embeds into (IHom(L,I), ⊓) as a topological semilattice;
- (L, +) embeds into (IA, ⊓) as a topological semilattice, for some set A;
- (L, +) embeds into a topological semilattice with small semilattices.
In order to show that a compact semilattice (L, +) does not have semilattices, it therefore suffices to show that (L, +) does not have enough interval homomorphisms. This is what Lawson did in [1], and his counterexample was presented in this post, although the rôle of interval homomorphisms was not made explicit there.
Many compact semilattices without small semilattices
Theorem D allows us to use the following technique to show that a compact semilattice (L, +) does not have small semilattices: find a topological semilattice embedding i of some compact semilattice (L’, +’) without small semilattices into (L, +).
Indeed, if (L, +) has small semilattices, then by, say, item 4 of Theorem D, there would be a topological semilattice embedding j of (L, +) into (IA, ⊓) for some set A. Then j o i would be a topological semilattice embedding of (L’, +’) into (IA, ⊓), and that does not exist if (L’, +’) does not have small semilattices, because of Theorem D.
Hence, for example, we obtain:
Proposition E. Given any compact semilattice (L, +) without small semilattices (e.g., Lawson’s), any product of (L, +) with any non-empty compact semilattice is a compact semilattice without small semilattices.
Indeed, let (L’, +’) be any non-empty compact semilattice. We pick any point e in L’; it does not matter which. The product of (L, +) with (L’, +’) is the topological product L” ≝ L × L’, with addition +” given by (x, x’) +” (y, y’) ≝ (x+y, x’+’y’). It is easy to see that (L”, +”) is a compact semilattice, and (L, +) embeds into (L”, +”) through the map x ↦ (x, e). It is an easy exercise to show that this is a topological semilattice embedding. Note, in particular, that associativity, commutativity, and idempotence all depend on the fact that e+’e=e, and that holds for any element e whatsoever.
This already gives us quite a lot of compact semilattices without small semilattices. Here is a way of getting even more.
Many more compact semilattices
We rely on the Hoare hyperspace construction, namely on the hyperspace of downwards-closed, closed subsets. This will require us to introduce and to recall quite a lot of results.
We start off with a pretty difficult theorem on the properties of general compact semilattices, which applies even without small semilattices. As before, a semilattice (L, +) has an underlying poset X, which has the same points as L, and whose ordering ≤ is defined by x≤y if and only if x=x+y. This is from the red book [4].
Proposition F (Proposition VI-6.25 [4]). Given a compact semilattice (L, +), its underlying poset X is a meet-continuous inf-semilattice, Xσ is stably compact, and (Xσ)patch = (L, ≤). In particular, Xσ = Lup, where Lup is L with the upward topology of the ordering ≤ on X.
An inf-semilattice is simply a poset with binary infima, and meet-continuous means that the binary infimum operation ⋀ on X (exists and) is Scott-continuous. Every continuous inf-semilattice is meet-continuous, but the converse implication fails. (The easiest counterexample is given by two copies of N with its usual ordering, put side by side and with an extra common bottom element and an extra common top element.)
The main difficulty in proving Proposition F is to show that every Scott-closed set is closed. Once this is done, the Scott topology on X will coincide with the upward topology on L, and the rest of the proposition can be proved by using Fact E, Fact F, Lemma G and Lemma H from this previous post on compact semilattices, realizing that their proofs depend only on (L, +) being a compact semilattice, and do not require small semilattices. As we have just said, the real difficulty is to show that every Scott-closed set is closed, and this can be proved in various ways.
One way consists in expressing limits limi ∈ I, ⊑ xi of nets in L as double limits inferior; explicitly, as liminff : N → I liminfn ∈ N xf(n). Since a limit inferior is a directed supremum of an infimum, every Scott-closed set is closed under limits inferior. Hence every Scott-closed set C will contain any limit of a net of elements of C, and hence will be closed (see Corollary 4.7.10 in the book). Now showing that limi ∈ I, ⊑ xi = liminff : N → I liminfn ∈ N xf(n) goes through a characterization of the topology of L as being generated by families of continuous subinvariant pseudo-metrics, and this relies on embedding (topologically, not as semilattices, otherwise Lawson’s theorem would tell you that L has small semilattices) L into products of intervals [0, 1]A, using Urysohn’s Lemma. All this occupies Section VI-2 of the red book [4].
Another way is described in Section VII-1 of the red book [4], and goes through the study of order-regular (o-regular) topologies, leading to more general results still.
Hence, sorry, but we will not give a proof of Proposition F here. But we will use it in conjunction with the following theorem, which was already mentioned and proved in this post on the comparison between the lower Vietoris and Scott topologies on the Hoare hyperspace H(Z) of a space Z. Let me recall that H(Z) is the set of all closed subsets of Z, ordered by inclusion. The lower Vietoris topology has a subbase of open sets of the form ◊U ≝ {F ∈ H(X) | F ∩ U ≠ ∅}, where U ranges over the open subsets of X, and is always coarser than the Scott topology of inclusion.
Theorem G [5, Proposition 3.9, Theorem 3.13]. If X is a poset in its Scott topology, which is either core-compact or first-countable, then the Scott topology coincides with the lower Vietoris topology on H(Xσ).
Let us recall that every stably compact space is locally compact, hence core-compact. With Proposition F, (and using the notations introduced there,) we obtain that the lower Vietoris and the Scott topologies coincide on H(Xσ), where Xσ = Lup. Since Lup is stably compact, so is H(Xσ), because of the following, which was mentioned and proved in this (now pretty ancient) post.
Proposition H. For every core-compact space Z, H(Z) is stably compact in its lower Vietoris topology.
From Proposition F, we have that X is a meet-continuous inf-semilattice. Every meet-continuous complete lattice is a meet-continuous topological space (a.k.a. a web space) in its Scott topology, as introduced in this post. The same proof (as the one given at the beginning of that post) shows that every meet-continuous inf-semilattice is meet-continuous as a topological space, too. Then, if you proceed to the next proposition in that post, and read item 5 of that proposition, you will see that for every meet-continuous space Z, H(Z) is also meet-continuous, as a complete lattice, namely that binary intersection is Scott-continuous on H(Z). Applying this observation on Z ≝ Xσ, and combining it with Propositions G and H, we obtain the following. (Oh yes, every stably compact space is locally compact, hence core-compact, so those two propositions do apply.)
Proposition I. Given a compact semilattice (L, +), with underlying poset X, H(Lup)=H(Xσ) is stably compact, its (lower Vietoris) topology coincides with the Scott topology of inclusion, and intersection ∩ is Scott-continuous on H(Xσ).
We will strengthen the latter and show that ∩ is not just Scott-continuous (i.e., separately continuous), but jointly continuous and in fact perfect. This will be Proposition K below, which one can find in [6, VII-1.8, bottom of page 276], and which can be proved with the help of the following lemma.
Lemma J. Let P be a dcpo with a Scott-continuous binary infimum operation ⋀. If Pσ is stably compact, then ⋀ is a perfect map from Pσ × Pσ to Pσ.
Proof. We observe that Pσ × Pσ coincides with (P × P)σ, where P × P is a product of posets, because Pσ is core-compact. Indeed, Pσ is core-compact if and only if the Scott and product topologies coincide on P × Y for every poset Y: this was the proposition mentioned in part 1(a) of the proof of Theorem 2 in this post on comparing the lower Vietoris and Scott topologies on Hoare hyperspaces.
Since ⋀ is Scott-continuous, it is continuous from (P × P)σ to Pσ, and therefore (jointly) continuous from Pσ × Pσ to Pσ.
In order to show that ⋀ is perfect, we need to show that the inverse image of a compact saturated subset Q by ⋀ is compact saturated, or equivalently that the inverse image of its complement P–Q is open in the de Groot dual (Pσ × Pσ)d of Pσ × Pσ. (The de Groot dual of a stably compact space is another stably compact space, with the same points, but with the cocompact topology; the latter is formed of the complements of the compact saturated sets, see Section 9.1 in the book.)
We therefore consider any two elements u and v of P, and we assume that u ⋀ v is in P–Q. Our aim is to find an open neighborhood U × V of (u, v) in (Pσ × Pσ)d entirely included in ⋀–1(P–Q), namely such that the infimum of any element of U with any element of V is in P–Q.
The downward closure ↓(u ⋀ v) is equal to ↓u ∩ ↓v, which is therefore included in P–Q. The latter is open in the de Groot dual (Pσ)d, and the ordering of a de Groot dual is reversed. Hence downward closure ↓u in P becomes upward closure in (Pσ)d; writing ↑d for upward closure in (Pσ)d (although that is just ↓), we therefore obtain that ↑du ∩ ↑dv is included in the open subset P–Q of (Pσ)d.
Now we remember that every stably compact space is weakly Hausdorff (yet another previous post will help! see the first Fact in that post), meaning that there are an open neighborhood U of u in (Pσ)d and an open neighborhood V of v in (Pσ)d such that U ∩ V is included in P–Q. Then U × V is open in (Pσ × Pσ)d, since its complement is equal to ((P–U) × P) ∪ (P × (P–V)), a union of two compact saturated sets. Also, U × V contains the pair (u, v). Finally, for every u’ in U and for every v’ in V, u’ ⋀ v’ ≤ u’, v’, and because U and V are upwards-closed in (Pσ)d, they are downwards-closed in P, so u’ ⋀ v’ is both in U and in V, hence in P–Q. ☐
Proposition K ([6, VII-1.8]). For every compact semilattice (L, +), (H(Lup)patch, ∩) is a compact semilattice.
Proof. First, H(Lup)patch makes sense and (H(Lup)patch, ⊆) is a compact pospace, by Proposition I. We claim that ∩ is perfect from H(Lup) × H(Lup) to H(Lup). Therefore it will be patch-continuous, and this will prove the proposition. We show that ∩ is perfect by applying Lemma J to P ≝ H(Lup) (as a poset, ordered by inclusion). Indeed, Pσ will coincide with H(Lup), its binary infimum operation ⋀ is intersection, and we have noticed that this is Scott-continuous in Proposition I. ☐
Many more compact semilattices without small semilattices
Now we have the following.
Theorem L. Let (L, +) be a compact semilattice. There is map η : L → H(Lup)patch, which sends every point x to its downward closure ↓x in Lup (namely, with respect to the ordering ≤ underlying (L, +)), and it is a topological embedding and a semilattice homomorphism.
As a consequence, if (L, +) does not have small semilattices, then (H(Lup)patch, ∩) does not have small semilattices either.
Proof. We claim that η is continuous, and for that we need a description of the patch topology on H(Lup). The open subsets of H(Lup) are unions of finite intersections of subsets of the form ♢U, with U open in Lup. We need to describe its compact saturated subsets.
Looking at the first post on the Hoare hyperspace, we see that H(Lup) is homeomorphic to O(Lup), the space of open subsets of Lup, with the lower topology, through the map ∁ that send every set to its complement. Additionally, the lower topology is the cocompact topology of O(Lup) with the Scott topology of inclusion; in other words, H(Lup) is homeomorphic through ∁ to the de Groot dual (O(Lup)σ)d. (Yes, that can make your head spin.) And finally, O(Lup) is a continuous complete lattice, because Lup is core-compact.
In fact, Lup is locally compact, so the way-below relation on O(Lup) is given by U ⋐ V if and only if U ⊆ Q ⊆ V for some compact saturated subset Q of Lup (Theorem 5.2.9 in the book). Since the Scott topology on a continuous dcpo has a base of the sets of the form ↟u (Theorem 5.1.17), it follows easily that the sets ■Q ≝ {V open in Lup | Q ⊆ V} form a base of the Scott topology on O(Lup), where Q ranges over the compact saturated subsets of Lup. Through the homeomorphism ∁, we obtain that the sets ■dQ ≝ {C ∈ H(Lup) | Q ⊆ Lup–C} = {C ∈ H(Lup) | Q does not intersect C} form a base of the cocompact topology on H(Lup). The complements of those sets can be written as ♢Q, since they are equal to {C ∈ H(Lup) | Q intersects C}. It follows that every compact saturated subset of H(Lup) is an intersection of sets of the form ♢Q, where Q is compact saturated in Lup.
Now η–1(♢Q) = Q, so the inverse image of any compact saturated subset of H(Lup) is an intersection of compact saturated sets in Lup, hence a compact saturated set since arbitrary intersections of compact saturated sets in a stably compact space are compact saturated. (In other words, any union of open sets in the de Groot dual of a stably compact space is open.)
It follows that the inverse image of any open subset of H(Lup)d is open in (Lup)d, and we started the proof by noting that the inverse image of any open subset of H(Lup) is open in Lup. Therefore the inverse image of any open subset of H(Lup)patch is open in (Lup)patch, namely in L. We have shown that η is continuous.
By the same token, any open subset O of L = (Lup)patch is a union of finite intersections of sets of open sets U of Lup and of complements Lup–Q of compact saturated subsets Q of Lup. We can write the first as η–1(♢U) and the second as η–1(H(Lup)–♢Q). Since η–1 commutes with unions and intersections, we can write O as the inverse image of some union V of finite intersections of sets of the form ♢U or H(Lup)–♢Q, and then V is open in H(Lup)patch. Clearly, (because L is T0,) η is injective, so η is a topological embedding.
Additionally, η is a semilattice homomorphism: we recall that + is binary infimum in Lup, so η(x+y) = η(x) ∩ η(y).
Hence, if (H(Lup)patch, ∩) has small semilattices, then there is a topological semilattice embedding f of (H(Lup)patch, ∩) into a compact semilattice of the form (IA, ⊓), by Lawson’s Theorem D. Then f o η is a topological semilattice embedding of (L, +) into (IA, ⊓), so by Lawson’s Theorem D again, (L, +) has small semilattices. By contraposition, if (L, +) does not have small semilattices, then (H(Lup)patch, ∩) does not have small semilattices either. ☐
Hence we can produce infinitely many compact semilattices without small semilattices from a given compact semilattice (L, +) without small semilattices, such as Lawson’s, either by taking a product with any compact semilattice, see Proposition E, or by applying the (H(_up)patch, ∩) construction, and repeating as many times as we wish.
Acknowledgments
The idea of Theorem L was communicated to the first author (Jean) both by Xiaodong Jia and the second author (Zhenchao).
- Jimmie D. Lawson. Lattices with no Interval Homomorphisms. Pacific Journal of Mathematics 32(2):459–465, 1970.
- Jimmie D. Lawson. Topological semilattices with small semilattices. J. London Math. Soc. (2), 1:719–724, 1969.Lawson, J.D. (1969). https://doi.org/10.1112/jlms/s2-1.1.719
- Andrea Schalk. Algebras for Generalized Power Constructions. PhD Thesis, TU Darmstadt, 1993.
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- Yu Chen, Hui Kou, and Zhenchao Lyu. Two topologies on the lattice of Scott closed subsets. Topology and its Applications, 306, 107918.
- Peter T. Johnstone. Stone spaces, Cambridge Studies in Advanced Mathematics Series 3, Cambridge University Press, 1982. ISBN 0-521-33779-8.
— Jean Goubault-Larrecq and Zhenchao Lyu (October 20th, 2023)

Goubault-Larrecq
