My purpose today is to explain a counterexample due to Jimmie Lawson [3], or rather a slight variant of it, pertaining to the theory of topological semilattices (which I will not assume to be Hausdorff, contrarily to [3]) and to a property that crops up naturally, namely having small semilattices. Before I can do this, I will have to spend some time explaining what topological semilattices are, and how small semilattices arise naturally.
Semilattices
A semilattice is a pair (L, +) where L is a set and + is an associative, commutative, and idempotent operator +. By idempotence, I mean that x+x=x for every x in L. Examples abound. Notably, there are sup-semilattices, which are posets in which every pair of elements x, y has a supremum x ⋁ y, in which case we can define + as ⋁; dually, there are inf-semilattices, in which every pair of elements x, y has an infimum x ⋀ y, in which case we define + as ⋀.
Every semilattice (L, +) has an associated ordering ⊑, defined by x⊑y if and only if x=x+y. Notice that, if we start from an inf-semilattice, we recover the original ordering this way. Conversely, this definition of ⊑ turns L into a poset, in which x+y is the infimum of x and y, for any two points x and y. Therefore semilattices are merely another presentation of inf-semilattices. (Or also of sup-semilattices, if you decide to take the opposite of ⊑ as your preferred ordering!)
Semilattices occur in a variety of other situations. Instead of making a comprehensive list, let me concentrate on one particular case where they arise naturally: the question of characterizing the algebras of the finitary Smyth hyperspace monad, as studied by Andrea Schalk [1]. That as well is something I need to introduce.
The finitary Smyth hyperspace Qfin(X)
For every topological space X, let the finitary Smyth hyperspace Qfin(X) be the set of non-empty finitary compact subsets of X, by which I mean the subsets of X of the form ↑{x1, …, xn}, where n≥1, and ↑ denotes upward closure with respect to the specialization preordering of X.
It is easy to see that (Qfin(X), ∪) is a semilattice. Its associated ordering ⊑ is defined by: Q is below Q’ if and only if Q = Q ∪ Q’, if and only if Q’ is included in Q. In other words, its associated ordering ⊑ is the familiar reverse inclusing ordering that we are accustomed to when handling Smyth powerdomains and their variants.
What other properties does it have?
We equip Qfin(X) with the upper Vietoris topology, whose basic open subsets are the sets ☐U ≝ {Q ∈ Qfin(X) | Q ⊆ U}, where U ranges over the open subsets of X. This is the subspace topology induced by the topology with the same name on the Smyth hyperspace Q(X); Q(X) is the set of all non-empty compact saturated subsets of X, whose basic open subsets I usually also write as ☐U, and are instead defined as {Q ∈ Q(X) | Q ⊆ U}. I am only considering Qfin(X) for now instead of Q(X) for simplicity.
With that topology, (Qfin(X), ∪) is even a topological semilattice. A topological semilattice is a semilattice (L, +) where L is given a topology such that + is jointly continuous. In the case of Qfin(X), we check that binary union is jointly continuous by verifying that ∪–1(☐U) is simply ☐U × ☐U.
Rather easily, Qfin(X) is T0, too: its specialization preordering is reverse inclusion.
Finally, for all elements Q and Q’ of Qfin(X), we always have Q ⊆ Q ∪ Q’, namely Q ∪ Q’ is below Q in the specialization ordering. The topological semilattices (L, +) in which x+y ≤ x for all points x and y, where ≤ is the specialization preordering of L (not the canonical ordering ⊑ defined from +) are called deflationary. You may compare this with the notion of inflationary semilattices, which we have looked at here.
Algebras of the Qfin monad
This raises the question whether (Qfin(X), ∪) would be the free T0 deflationary topological semilattice over the space X. For that question to make sense, we need to define a category of T0 deflationary topological semilattices, with continuous, addition-preserving maps as morphisms, and we ask whether the forgetful functor from that category to the category Top0 of T0 topological spaces has a left adjoint.
Let us approach the problem in a different way. If (Qfin(X), ∪) were the free T0 deflationary topological semilattice over X, then the required adjunction would produce a monad (T, η, μ) on Top0 such that TX=Qfin(X) for every space X, at least up to natural isomorphism. We already know of such a monad: the unit ηX : X → Qfin(X) maps every point x of X to ↑x, and the multiplication μX : Qfin(Qfin(X)) → Qfin(X) maps every element Q of Qfin(Qfin(X)) to ∪Q, the union of all the elements of Q; explicitly, μX(↑{↑E1, …, ↑En}) = ↑(E1 ∪ … ∪ En). (I will let you check that this is indeed a monad by yourself.)
Then we characterize the algebras of that monad. The category Top0Qfin of Qfin-algebras, also known as the Eilenberg-Moore category of the monad, is automatically equipped with an adjunction, which turns Qfin(X) into the free Qfin-algebra over the T0 space X. Our question then becomes: are the Qfin-algebras on Top0 exactly the T0 deflationary topological semilattices?
This was studied, among other things, by Andrea Schalk [1]. One can check that every Qfin-algebra has a canonical structure of deflationary topological semilattice, but not all deflationary topological semilattices give rise to a Qfin-algebra. The reasons are the following, and I will explain them below.
- Every Qfin-algebra is a deflationary topological semilattice with small semilattices. (Ah, at last! We finally meet the small semilattices. In fact, the Qfin-algebras are exactly the deflationary topological semilattices with small semilattices.)
- There is a deflationary topological semilattice that does not have small semilattices, as shown by Jimmie Lawson [3] (see also [2, Section VI-4]). This is actually the main thing I would like to explain here; the rest is mostly motivation for this, if you remember what I said in the introduction.
Of course, I haven’t said yet what having small semilattices means. Here we go.
A subsemilattice of a semilattice (L, +) is just a subset A of L that is closed under addition: for all x, y in A, x+y is in A. A topological semilattice (L, +) has small semilattices if and only if every point has a neighborhood base consisting of semilattices, namely if and only if:
- for every x ∈ L, for every open neighborhood U of x, there is a subsemilattice A of L such that x ∈ int(A) ⊆ A ⊆ U.
Every Qfin-algebra is canonically a T0 deflationary topological semilattice with small semilattices
Let us check the first of our claims: every Qfin-algebra (on Top0) is a T0 deflationary topological semilattice with small semilattices. For that, we need to remember that a Qfin-algebra (on Top0) is a T0 topological space L together with a so-called structure map α : Qfin(L) → L such that:
- α o ηL = idL, namely α(↑x)=x for every x in L;
- α o μL = α o Qfin(α). The action of the functor Qfin on morphisms f is defined by Qfin(f) : ↑{x1, …, xn} ↦ ↑{f(x1), …, f(xn)}, so we require that α(↑(E1 ∪ … ∪ En)) = α(↑{α(↑E1), …, α(↑En)}) for every n≥1 and all finite non-empty sets E1, …, En.
There is a canonical way of defining a semilattice structure on such a Qfin-algebra L: we let x+y ≝ α(↑{x, y}). Then x+x = α(↑x) = x, so + is idempotent. It is commutative by definition. In order to show that + is associative, we apply the law α(↑(E1 ∪ … ∪ En)) = α(↑{α(↑E1), …, α(↑En)}) to the case n≝2, E1≝{x, y}, E2≝{z}, yielding α(↑{x,y,z}) = (x+y)+z, and to the case n≝2, E1≝{x}, E2≝{y, z}, yielding α(↑{x,y,z}) = x+(y+z).
This is a topological semilattice, because + is the composition of ηL × ηL, of the binary union operation ∪ (which, as we have seen already, is jointly continuous on Qfin(L)), and of α.
Note that the law α(↑(E1 ∪ … ∪ En)) = α(↑{α(↑E1), …, α(↑En)}) can now be interpreted, when n=2, as saying that α maps unions to sums, namely α(↑E1 ∪ ↑E2) = α(↑E1) + α(↑E2).
Finally, L has small semilattices. Let x be any point of L, and U be any open neighborhood of x in L. We have α(↑x)=x, so ↑x is in the open subset α–1(U) of Qfin(L). By definition of the upper Vietoris topology, there is an open subset V of X such that ↑x is in ☐V, and ☐V is included in α–1(U). Now we notice that:
- x is in V, since ↑x is in ☐V;
- ☐V is a sub-semilattice of Qfin(L): the union of any two elements of ☐V is again in ☐V;
- the direct image A ≝ α[☐V] of ☐V is a sub-semilattice of L: indeed, ☐V is closed under binary unions, and α maps unions to sums;
- V is included in A: for every point y of V, ↑y is in ☐V, so y=α(↑y) is in A, by definition of A;
- A is included in U: in other words, α[☐V] ⊆ U, and that is equivalent to ☐V ⊆ α–1(U), which is by construction.
In short, x ∈ V ⊆ A ⊆ U. Therefore L has small semilattices, as promised.
Qfin-algebras = T0 deflationary topological semilattices with small semilattices
We have proved one half of the equivalence between Qfin-algebras and T0 deflationary topological semilattices with small semilattices. In the other direction, let (L, +) be a T0 deflationary topological semilattice with small semilattices. We show that there is a unique Qfin-algebra structure on L, namely a unique structure map α : Qfin(L) → L that is compatible with +, in the sense that α(↑{x, y}) = x+y for all points x, y of L.
Well, we do not have much choice: we must define α(↑{x1, …, xn}) as the sum x1+ …+xn. Showing that this makes sense makes heavy use of the fact that + is associative, commutative, idempotent, and deflationary.
There only remains to show that this map α is continuous, and this is where we require (L, +) to be topological, and to have small semilattices. Let ↑{x1, …, xn} be mapped by α to a point (necessarily x1+ …+xn) in some open subset U of L. We wish to show that there is an open neighborhood of ↑{x1, …, xn} in Qfin(L)—which we shall take of the form ☐V, with x1, …, xn all in the open set V—that is mapped by α into U.
Here is how we might think of proceeding, hoping to use only joint continuity, not small semilattices. Since + is jointly continuous, there is a product U1 × … × Un of open neighborhoods of x1, …, xn respectively, such that every sum of n elements, one from U1, …, one from Un, lies in U. We might think of defining V as some kind of intersection, or of union, or of sum of the open sets U1, …, Un, but none of that works, really. Notably the sum U1 + … + Un, which we define as the set of sums of n elements, one from U1, …, one from Un, is not open in general—at least there is no reason why it should be.
Instead, we first use the fact that L has small semilattices: there is a sub-semilattice A of U such that x1+ …+xn is in the interior int(A) of A. Now (and only now) we use the fact that + is jointly continuous, so there is a product U1 × … × Un of open neighborhoods of x1, …, xn such that the sum U1 + … + Un is included in int(A). We define V as int(A).
- It is easy to see that ↑{x1, …, xn} is in ☐V, namely that every xi is in int(A): this is because + is deflationary, so that xi ≥ x1+ …+xn, and because x1+ …+xn is in the open, hence upwards-closed, set int(A).
- For every non-empty finitary compact set ↑{y1, …, ym} in ☐V, all the points yj are in V, hence in A, and therefore their sum y1+ …+ym is also in A, because A is a sub-semilattice. Since A is included in U, this means that α maps ☐V into U, and this finishes to show that α is continuous.
A T0 deflationary topological semilattice that does not have small semilattices
At this point, you should be convinced that the notion of having small semilattices arises naturally. But is that a useful notion? Namely, if all T0 deflationary topological semilattices had small semilattices, that would be a useless notion.
Be reassured: there is a T0 deflationary topological semilattice that does not have small semilattices. Such a counterexample was found by Jimmie Lawson [3]. Well, let me be slightly more precise. What J. Lawson found was really an example of a compact Hausdorff topological semilattice that does not have small semilattices (and I will come back to that further below), but this can easily be modified to an example of a T0 deflationary topological semilattice that does not have small semilattices. That is no accident either: this is due to the so-called fundamental theorem of compact semilattices, which I will briefly mention near the end of this post.
Let me describe that counterexample. In passing, I will also simplify it somehow. J. Lawson uses a funny divergent series, but I think the functions I will introduce below make the argument slightly less obscure. Also, his spaces Si are defined as certain finite products of {0, 1}, but I think it will be clearer to describe them as powersets.
We will build that counterexample in several steps: we build a very slowly growing function (Fact (i) below), which we use to show that a certain measure of finite sets has the property that the intersection of any two big sets, with respect to that measure, remains big enough (Fact (ii) below), and we will have what it takes to finally define our counterexample
A very slowly growing function
Let log2 denote base 2 logarithm, so that log2(2x)=x for every non-negative real number x. This is a slowly growing function, which tends to infinity as its argument tends to infinity. The map x ↦ log2 log2 x is an even more slowly growing function. It maps [2, ∞[ to [0, ∞[, and also grows to infinity as its argument tends to infinity, but painfully slowly. Here is a plot of that function:
The point of choosing the log2 log2 function is that it grows so slowly to infinity that the following holds. That will be crucial to establishing Fact (ii) below, which in turn will be the key to the joint continuity of the semilattice operation.
- Fact (i). For every ε>0, there is a natural number kε≥2 such that for every k≥kε, log2 log2 (1+k) + ε > log2 log2 (1+2k).
Let us check this: the inequality log2 log2 (1+k) + ε > log2 log2 (1+2k) is equivalent to log2 (1+k).2ε > log2 (1+2k), hence to 2ε > log2 (1+2k)/log2 (1+k). As k tends to infinity, log2 (1+2k)/log2 (1+k) ~ 1+ 1/log2 k, which will be smaller than any fixed number >1 (such as 2ε) for k large enough. If you prefer an explicit definition, I will let you check that defining kε as 21/(2ε-1) works, as in that case we even have 2ε > log2 (2+2k)/log2 (1+k) (=1/log2 (1+k) + 1) for every k≥kε. ☐
We now define the finite set Ni as the set of all positive natural numbers strictly smaller than 22i, for every natural number i, namely:
Ni ≝ {1, …, 22i–1}.
Let Si be the powerset of Ni, seen as a dcpo with the inclusion ordering. Notice that Si is an incredibly well-behaved dcpo. In fact it is a finite dcpo, in particular an algebraic dcpo, in which all elements are themselves finite. It is also a (complete) lattice.
Measuring elements of Si in such a way that the intersection of any two big sets remains big enough
We define a kind of measure of size of the elements E of Si, by defining the following extended non-negative real number σi(E): if E is the whole of Ni, then σi(E)=∞; otherwise, we let:
σi(E) ≝ i–log2 log2 (22i–|E|),
where |E| denotes the cardinality of E. Alternatively, σi(E) = i–log2 log2 (1+|Ni–E|).
Notice that, when E is equal to Ni minus one element, then |Ni–E|=1, so σi(E) = i–log2 log2 2 = i; while if E is empty, σi(E) = i–log2 log2 (22i) = 0.
It is clear that σi is a monotonic map from Si to [0, ∞], hence a Scott-continuous map (since Si is finite!). In fact, we have the stronger property that if E and F are any two elements of Si such that |E| ≤ |F|, then σi(E) ≤ σi(F).
Here is a plot of σi(E) as a function of |E| when i=3, growing from σ3(∅)=0 to σ3(E)=3 when |E|=254. (The value σ3(E)=∞ when |E|=255, namely when E=N3, is not shown.)
They key property of the maps σi is the following.
- Fact (ii). For all real numbers τ > ε > 0, there is a natural number iτ,ε such that for every i≥iτ,ε, for all elements E and F of Si such that σi(E) > τ and σi(F) > τ, we have σi(E ∩ F) > τ–ε.
In other words, the intersection of any two “big” subsets of Si (as measured through the function σi) will remain “big”, up to some small ε, and this for every index i that is large enough.
Let us verify Fact (ii). Not that I would want to spoil the surprise, but we will define iτ,ε as τ + log2 log2 (1+2kε), where kε was introduced in Fact (i). If E is equal to the whole of Ni, then E ∩ F = F, and Fact (ii) is trivial; similarly if F=Ni. Hence we will assume that |Ni–E|≥1 and |Ni–F|≥1. We also reason by contradiction, and we assume that σi(E ∩ F) ≤ τ–ε for some i≥iτ,ε. This means that i – log2 log2 (1+|Ni–(E ∩ F)|) ≤ τ–ε.
We have |Ni–(E ∩ F)| = |(Ni–E) ∪ (Ni–F)| ≤ |Ni–E| + |Ni–F| ≤ 2k, where k ≝ max (|Ni–E|, |Ni–F|). Therefore τ–ε ≥ i – log2 log2 (1+|Ni–(E ∩ F)|) ≥ i – log2 log2 (1+2k). Since i ≥ iτ,ε = τ + log2 log2 (1+2kε), it follows that τ–ε ≥ τ + log2 log2 (1+2kε) – log2 log2 (1+2k), namely that log2 log2 (1+2k) ≥ log2 log2 (1+2kε) + ε. In particular, k≥kε.
This enables us to use Fact (i): so log2 log2 (1+k) + ε > log2 log2 (1+2k). Recalling that |Ni–(E ∩ F)| ≤ 2k, it follows that σi(E ∩ F) = i – log2 log2 (1+|Ni–(E ∩ F)|) ≥ i – log2 log2 (1+2k), so σi(E ∩ F) > i – log2 log2 (1+k) – ε. Now k = max (|Ni–E|, |Ni–F|), so k is equal to |Ni–E| or to |Ni–F|. Let us assume that k=|Ni–E|. We have just shown that σi(E ∩ F) > i – log2 log2 (1+|Ni–E|) – ε = σi(E) – ε > τ – ε, which is impossible. The case where k=|Ni–F| is symmetric. ☐
Building the counterexample L
We will build our counterexample L as a subspace of the following nice space K: K is the product of [0, ∞] (with its Scott topology) with S0, S1, …, and so on. Recall that Si is the powerset of Ni, also in its Scott topology, and that Ni={1, …, 22i–1}. K is a product of continuous dcpos, all of which have a least element, so K is itself a continuous dcpo, and the Scott topology on K is also the product topology of the Scott topologies on [0, ∞], S0, S1, … (see Proposition 5.1.56 in the book.) K is also a complete lattice, in which suprema and infima are computed componentwise. This is a space with very nice properties.
We define L as the subspace of K consisting of those tuples (s, A0, A1, …) such that s≤σi(Ai) for every i≥0.
Please mind the fact that the topology of L is the subspace topology, not the Scott topology of the componentwise ordering.
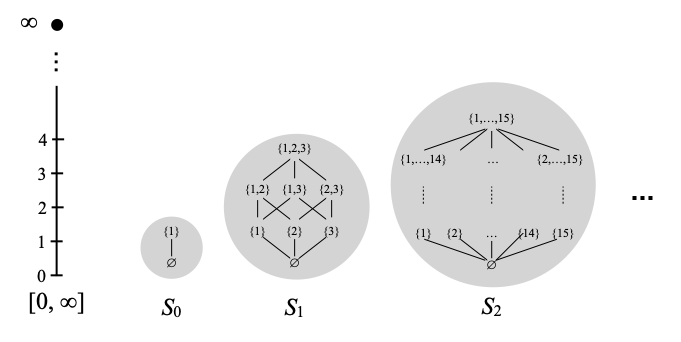
In order to understand what the points of L are, let me suggest the following explanation. (Please refer to the picture below.) In order to choose a point in L, one way is to pick an arbitrary element A0 of S0, an arbitrary element A1 of S1, and so on; then we pick s ∈ [0, ∞] in such a way that s≤σ0(A0), s≤σ1(A1), etc. In the example below, I have chosen A0 as the top element {1} of S0, and the associated constraint s≤σ0(A0) is vacuous (equivalent to s≤∞). I have then chosen A1 as {1, 3} in S1; then σ1(A1)=1, so that forces s≤1. Next, I have chosen A2 as {1,3,4,6,7} in S2; then σ2(A2) is roughly 0.21, and s has to be at most that. And so on, and so forth.
The specialization ordering of K is componentwise: (s, A0, A1, …) ≤ (t, B0, B1, …) if and only if s≤t, A0⊆B0, A1⊆B1, etc. Therefore the specialization ordering of L is also componentwise, and I will write ≤ for it.
Let me observe that, with that ordering, L is an inf-semilattice. The infimum (s, A0, A1, …) ⋀ (t, B0, B1, …) is (u, C0, C1, …) where:
- Ci ≝ Ai ∩ Bi for every i≥0;
- u ≝ min(s, t, infi≥0 σi(Ci)).
The term infi≥0 σi(Ci) in the definition of u is, of course, due to the fact that we require u to be smaller than or equal to every σi(Ci), if (u, C0, C1, …) is to be an element of L.
With that operation, it is clear that (L, ⋀) is a deflationary semilattice, and we must show that it is a topological semilattice, namely that ⋀ is jointly continuous from L × L to L.
The ⋀ operation is jointly continuous on L
In order to show this, we realize that a base of the topology of K is given by sets of the form U × ↑E0 × ↑E1 × … × ↑En × Πi>n Si where U is Scott-open in [0, ∞] (hence equal to the whole of [0, ∞] or of the form ]r, ∞] for some r>0), n≥0, and each Ei is a (necessarily finite) subset of Si for each i, 0≤i≤n. Hence a base of the topology of L is given by the corresponding sets L ∩ (U × ↑E0 × ↑E1 × … × ↑En × Πi>n Si).
Let therefore (s, A0, A1, …) and (t, B0, B1, …) be two points of L, whose infimum (u, C0, C1, …), given as above, lies in some basic open set W ≝ L ∩ (U × ↑E0 × ↑E1 × … × ↑En × Πi>n Si). We wish to find an open rectangle around the pair of points (s, A0, A1, …) and (t, B0, B1, …), and which would be mapped into W by ⋀.
- If U = [0, ∞], this is easy: we simply take W × W for that open rectangle. We do not need to care about the first components, which will always fall inside U; for every i≥0 with i≤n, Ci contains Ei, so both Ai and Bi contain Ei (since Ci = Ai ∩ Bi), and conversely, the intersection of any two sets that both contain Ei still contains Ei.
- We now examine the case where U is equal to ]r, ∞] for some r>0. Our assumption that (u, C0, C1, …) is in W can be rephrased as, first:
(a) for every i with 0≤i≤n, Ai and Bi contain Ei.
Second, u = min(s, t, infi≥0 σi(Ci)) > r, which means that there is a positive number τ such that r < τ < min(s, t, infi≥0 σi(Ci)), or explicitly:
(b) r<τ (c) τ<s,t (d) for every i≥0, τ<σi(Ai ∩ Bi).
Let ε>0 be such that r < τ–ε (thanks to (b)). Considering the number iτ,ε obtained in Fact (ii), we let m ≝ max(n, iτ,ε). The desired open rectangle is the product of V1 ≝ L ∩ (]τ, ∞] × ↑A0 × ↑A1 × … × ↑Am × Πi>mSi) and of V2 ≝ L ∩ (]τ, ∞] × ↑B0 × ↑B1 × … × ↑Bm × Πi>mSi). It is clear that (s, A0, A1, …) is in V1 and that (t, B0, B1, …) is in V2, using (b). It remains to verify that for every pair of points (s‘, A‘0, A‘1, …) in V1 and (t‘, B‘0, B‘1, …) in V2, their infimum (u‘, C‘0, C‘1, …) is in W.
By definition, C‘i = A‘i ∩ B‘i for every i≥0, and u‘ ≝ min(s‘, t‘, infi≥0 σi(C‘i)). We have:- for every i≥0, A‘i contains Ai, B‘i contains Bi, so C‘i = A‘i ∩ B‘i contains Ai ∩ Bi, which contains Ei by (a);
- s’>τ and t’>τ; for every i≥0, either i≤m, and then σi(C‘i) ≥ σi(Ai ∩ Bi) (since σi is monotonic) > τ by (d); or i>m, in particular i≥iτ,ε, so by Fact (ii) (this is the whole point of the construction!), and using the fact that τ<σi(Ai ∩ Bi)≤σi(Ai),σi(Bi), we obtain that σi(Ai ∩ Bi)>τ–ε. Putting all those inequalities together, u‘ = min(s‘, t‘, infi≥0 σi(C‘i)) > min(τ, τ–ε) = τ–ε > r. And we are done!
This finishes the proof of:
Lemma. (L, ⋀) is a deflationary topological semilattice.
L is also T0. In fact, with some extra effort, one can show that L is stably compact. (Hint: K is a product of stably compact spaces, hence is itself stably compact. Then L is a patch-closed subset of K, owing to the fact that each of the maps σi is patch-continuous… for the trivial reason that the patch topology on each Si is the discrete topology.) Also, one can show that L is not just an inf-semilattice, but in fact a complete lattice. (Beware, though, that its topology is most likely not the Scott topology. I have thought about it, and while I have no proof of it, I doubt that the topology would be the Scott topology.)
No small semilattices for L
Despite this niceness, we have:
Lemma. (L, ⋀) does not have small semilattices.
Proof. Let us consider any sub-semilattice A of (L, ⋀) whose interior contains the top element ⊤ ≝ (∞, N0, N1, …). That interior contains a basic open subset W ≝ L ∩ (U × ↑E0 × ↑E1 × … × ↑En × Πi>n Si), for some Scott-open subset of [0, ∞], etc. For every k ∈ Nn+1, let zk be the point (∞, N0, N1, …, Nn, Nn+1–{k}, Nn+2, …); namely it differs from the top element only at coordinate n+1, where we remove the single number k. The point zk is in W. Moreover, since Nn+1 is finite (that is crucial!), the sum (=infimum) of all the points zk, k ∈ Nn+1, is a finite sum. Since all the points zk are in W, hence in A, that sum is also in A. Let us write (s, A0, A1, …) for that sum. We see that Ai=Ni for every i≠n+1, but that does not matter. What does matter is that An+1 is the intersection of the sets Nn+1–{k} when k ranges over Nn+1, hence is empty. It follows that s≤σn+1(∅), namely that s=0.
Hence we have just proved that any sub-semilattice A whose interior contains ⊤ must contain an element (s, A0, A1, …) such that s=0. It follows that no basic open subset of the form L ∩ (]r, ∞] × ↑E0 × ↑E1 × … × ↑En × Πi>n Si) with r>0 can contain any sub-semilattice A that would be a neighborhood of ⊤. Hence (L, ⋀) does not have small semilattices. ☐
As a consequence, (L, ⋀) cannot be equipped with the structure of a Qfin-algebra. Let us (re)explain why. If there were a structure map α : Qfin(L) → L of a Qfin-algebra, α would have to map every non-empty finitary compact subset ↑{z1, …, zn} of L to the sum, namely to the infimum z1 ⋀ … ⋀ zn. But that map is not continuous (despite the fact that binary infimum ⋀ is continuous). Explicitly, if α were continuous, then the inverse image of the open set L ∩ (]r, ∞] × Πi≥0 Si) would be an open neighborhood of ↑{⊤}. Hence it would contain an open subset of the form ☐W, for some open neighborhood W of ⊤ in L. Taking zk as in the proof of the Lemma above, which are all in W, ↑{z1, …, zn} would be in ☐W hence in α–1(L ∩ (]r, ∞] × Πi≥0 Si)); but α(↑{z1, …, zn}) = z1 ⋀ … ⋀ zn is of the form (s, A0, A1, …) where s=0, which is impossible.
Lawson’s counterexample
The stably compact, deflationary topological semilattice (L, ⋀) is, in fact, not Lawson’s counterexample [3], but it is not far away!
Jimmie Lawson had proposed his counterexample in order to answer a conjecture of Dyer and Shields in the negative. I will refer you to [3] for that aspect of things. It is obtained as a Rees quotient of another topological semilattice (L’, ≤), which is a variant of (L, ≤), and which I will describe below.
In order to motivate (L’, ≤), I should say that perhaps the most interesting aspect of the theory of semilattices with small semilattices is the so-called fundamental theorem of compact semilattices [2, Theorem VI-3.4], which states an equivalence of categories between the category of compact Hausdorff semilattices with small semilattices on the one hand, and the category of bc-domains on the other hand. I will perhaps explain that one another time. That was found way earlier than everything else I have mentioned here, even before the term “bc-domain” was even coined. It is a pretty amazing result, too, in the sense that it says that a special form of continuous dcpo (bc-domains) arises from a situation with a priori no domain theory in it: a class of (compact) Hausdorff spaces, with a certain algebraic operation + on it.
Nowadays, Lawson’s counterexample serves mostly to show that there are compact Hausdorff semilattices that do not have small semilattices. Here it is.
Let L’ consist of the same set of points as L, but with the subspace topology induced by the inclusion in Kpatch. I have already hinted that K is stably compact. Hence its patch space (Kpatch, ≤) is a compact pospace (see Section 9.1 in the book). I have also hinted that L’ is closed in Kpatch. Therefore (L’, ≤) is also a compact pospace. In particular, L’ is a compact Hausdorff space.
One can show that (L’, ⋀) is also a topological semilattice, but beware that ⋀ is no longer the infimum operation corresponding to the specialization ordering of L’! In fact, since L’ is Hausdorff, the specialization ordering of L’ is simply equality, and therefore no two distinct elements have an infimum. For the same reason, (L’, ⋀) is certainly not a deflationary topological semilattice.
In order to see that (L’, ⋀) is a topological semilattice, one needs to show that ⋀ is jointly continuous on L’. The easiest way to show this is to realize that the topology of L’ is generated by the open subsets of L, plus sets of the form L ∩ (U × ↓E0 × ↓E1 × … × ↓En × Πi>n Si) where U is of the form [0, r[ or equal to the whole of [0, ∞]. Those sets L ∩ (U × ↓E0 × ↓E1 × … × ↓En × Πi>n Si) generate a dual topology on L, and I will call Lop the space L with that dual topology: that is simply the Scott topology of the opposite ordering. (As a side note, the patch topology on K is the product of the patch topologies on each component, and it has basic open subsets of the form I × {E0} × {E1} × … × {En} × Πi>n Si, where I is an interval of the form [0, b[, ]a, b[, ]b, ∞], or [0, ∞], but using that kind of base will force you to replay most of the arguments we have already done. Instead, it is easy to see that the topology generated by the sets I × {E0} × {E1} × … × {En} × Πi>n Si coincides with that generated by the sets U × ↑E0 × ↑E1 × … × ↑En × Πi>n Si where U is open and upwards-closed in [0, ∞], and by the sets U × ↓E0 × ↓E1 × … × ↓En × Πi>n Si where U is open and downwards-closed in [0, ∞].) Then, since we already know that ⋀ is jointly continuous on L, it suffices to show that it is also jointly continuous on Lop. I will let you verify this. This is much easier than the continuity of ⋀ on L, and in particular does not require fancy arguments such as Fact (ii).
Hence (L’, ⋀) is a compact Hausdorff, topological semilattice. By similar arguments as with (L, ⋀), it does not have small semilattices; to be precise, the argument is the same, simply replace ↑Ei by {Ei}.
Conclusion
The notion of semilattices with small semilattices occurs naturally in several places. The last place I have mentioned here is the fundamental theorem of compact semilattices, which I may talk about at more length another time. My first motivating example was Schalk’s characterization of the algebras of the finitary Smyth hyperspace monad Qfin on Top0.
Here is another case where small semilattices come into play.
For a sober space X, the sobrification of Qfin(X) is the space Qs(X) of so-called strong non-empty compact saturated subsets of X, not Q(X) as one might expect [1, Proposition 7.33]. Strong compact sets were initially introduced by Reinhold Heckmann [4], and I should definitely say a word about them some time! Then Qs also defines a monad on the category of sober spaces, and its algebras are exactly the deflationary sober semilattices with small semilattices [1, Theorem 7.37]. The proof is a pretty simple extension of what we have done with Qfin.
- Andrea Schalk. Algebras for Generalized Power Constructions. PhD Thesis, TU Darmstadt, 1993.
- Gerhard Gierz, Karl Heinrich Hofmann, Klaus Keimel, Jimmie D. Lawson, Michael W. Mislove, and Dana S. Scott. Continuous Lattices and Domains. Number 93 in Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, 2003.
- Jimmie D. Lawson. Lattices with no Interval Homomorphisms. Pacific Journal of Mathematics 32(2):459–465, 1970
- Reinhold Heckmann. An upper power domain construction in terms of strongly compact sets. In: Brookes, S., Main, M., Melton, A., Mislove, M., Schmidt, D. (eds) Mathematical Foundations of Programming Semantics. MFPS 1991. Lecture Notes in Computer Science, vol 598. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-55511-0_14

— Jean Goubault-Larrecq (April 19th, 2022)