Sheaves and streams I: sheaves of locally monotone maps

Let us talk about sheaves. My point is that you can play a few tricks with streams using sheaf technology. None of what I will say about sheaves is new, but the tricks I play between sheaves and streams are new. I have too much to say for just one post, so consider the present post as an introduction for things to come.

Oh, wait. If you already know about sheaves, do not expect too much from me. I will only talk about the most mundane notion of sheaves here, namely sheaves of sets over a topological space X. There are far-reaching generalizations of those notions. For example, we only really use the frame OX of open subsets of X to define a sheaf over X, so one should really define sheaves of sets over a locale L. There is nothing really special about locales here (from the outset), and one can define sheaves over posets, and in fact over small categories, with a so-called Grothendieck topology, forming so-called sites. You can also form sheaves of vector spaces or of modules instead of sets, and so on. If you wonder about those, go read MacLane and Moerdijk’s textbook [1]. But, as I said, I will simply work with the mundane notion of sheaves, those that sit above a topological space X, and sheaves of sets only, too.

Presheaves

We start with presheaves. Sheaves will be certain kinds of presheaves. A presheaf over a topological space X is given by:

• a collection of sets F_U, one for each open subset U of X;
• for each pair of open subsets U, V of X such that U ⊆ V, a so-called restriction map r_UV : F_V → F_U
• such that, whenever U ⊆ V ⊆ W, r_UV o r_VW = r_UW
• and such that for every open subset U of X, r_UU is the identity map.

A category theorist would simply say that such a presheaf over X is a functor from OX^op to Set, relying on the fact that every poset, and in particular OX, can be seen as a category. That is a much more elegant definition, but perhaps one that is harder to grasp the first time around.

Here are a few examples.

Sheaves

• If we define F_U as the set of all continuous maps from U to some fixed topological space R, then it is natural to define the restriction map r_UV as sending each continuous map f : V → R to its restriction f_|U to the smaller set U. This is a presheaf, the presheaf of locally continuous maps from X to R.
• If X is a manifold (for now, just a topological space with a well-behaved notion of differentiation on it, whatever that means), then we can instead define F_U as the set of all differentiable maps from U to the space R of real numbers, and restriction is defined as above.
• The last two examples are very classical. Here is a new one, which really follows exactly the same logic. Recall that a prestream is a pair (X, (⊑_U)_{U ∈ OX}) of a topological space X and a precirculation (⊑_U)_{U ∈ OX}. A precirculation is a collection of preorderings ⊑_U on U, one for each open subset U of X, with the following monotonicity property: if U ⊆ V, then for all points x, y of U such that x ⊑_U y, we also have x ⊑_V y. This can be seen as an axiomatization of the notion of local direction of time.
  Given a poset P (whose ordering I will write as ≤), we can define F_U as the set of monotone maps from U to P; its elements are the maps f : U → P such that, for all points x, y of U such that x ⊑_U y, f(x)≤f(y).
  The restriction map r_UV is defined as usual, by r_UV(f)≝f_|U for all open sets U ⊆ V and monotone maps f : V → P. Note that f_|U is indeed a monotone map from U to P, although the preordering on U may fail to coincide with the restriction of that on V to U: for all points x, y of U such that x ⊑_U y, the monotonicity property of precirculations entails that x ⊑_V y, so that f(x)≤f(y).
  Let me call this example the presheaf of locally monotone maps from the prestream (X, (⊑_U)_{U ∈ OX}) to P.
• A variant of the latter construction is the presheaf of locally monotone continuous maps from the prestream (X, (⊑_U)_{U ∈ OX}) to P, where F_U is now the set of monotone maps from U to P that are also continuous. In that case, we need P to be a poset with some topology on it, whatever it is.

All those examples are really sheaves, which are presheaves with the following additional property (which I will write on several lines to allow you to pause between quantifications, and to digest the various components as you ingest them):

• for every open subset U of X,
• for every open cover C of the subspace U (namely, each V ∈ C is open in X and included in U, and their union is the whole of U [added, Dec. 18, 2022]),
• for every consistent family of elements f_V ∈ F_V, one for each element V of the cover C,
• there is a unique element f_U ∈ F_U whose restriction to each open set V in C is f_V.

A family (f_V)_{V ∈ C} is consistent if and only if, for all V and W in C, f_V and f_W have the same restriction to V ∩ W, namely r_{(V ∩ W)V}(f_V)=r_{(V ∩ W)W}(f_W).

Let me explain. If we are given an element f ∈ F_U (think of it as a map from U to some set, as in the examples given earlier), and an open cover C of the subspace U, we can form the elements f_V≝r_VU(f). One can glue back the elements f_V together to form f: when those elements are functions, f maps every element x of U to f_V(x), where x is any element V of C that contains x. One can do this because the maps f_V are consistent, namely, for every point x of U, if x happens to belong to two elements V and W of C, then f_V(x)=f_W(x). Equivalently, for all elements V and W of C, f_V and f_W have the same restriction to V ∩ W. A presheaf in which you can glue back consistent families (in a unique way!) is a sheaf.

The sheaf of locally continuous maps on X to some fixed topological space R is an important example. As we will see next time (and as is well known), every sheaf on X can be seen up to some form of isomorphism as a sheaf of (certain) locally continuous maps on X (the so-called local sections of a local homeomorphism). By the way, that should be intriguing: for example, this certainly applies to the sheaf of locally monotone maps from a stream.

It is sometimes easier to understand a concept through counterexamples. A constant presheaf (with value a given set E) on a topological space X is given by defining each F_U as the set of constant maps from U to E. When U is non-empty, we can equate any constant function with its value, so that we can safely equate F_U with E itself. When U is empty, there is exactly one (constant) function from ∅ to E, so F_∅ is a one element set. Although that might seem surprising at first, that is almost never a sheaf. In order to see this, consider two disjoint, non–empty open sets V and W. They form an open cover of U≝V ∪ W. Now define f_V as the constant map with value, say, 1, and f_W as the constant map with value 2. Those form a consistent family, simply because V ∩ W is empty. All right, but surely both f_V and f_W are restrictions, to V and W respectively, of a unique map f from U to E, right? The point is that f is not a constant map, as specified in the definition of the constant presheaf.

That might ring a bell. We had had a similar issue with prestreams here. Explicitly, we had realized that every topological space with a preordering gave rise to a prestream, which was almost never a stream. And indeed, the presheaf of locally monotone maps from a prestream to a poset P will almost never be a sheaf… unless the prestream is a stream, which is what we show next.

When is the presheaf of locally monotone maps of a prestream a sheaf?

Oh, right, what is a stream? Of course, I have already said what it is there. But let me repeat. That is a prestream (X, (⊑_U)_{U ∈ OX}) whose precirculation (⊑_U)_{U ∈ OX} is a circulation:

• for every open subset U of X,
• for every cover C of the subspace U,
• for all points x, y in U,
• x ⊑_U y if and only if there are finitely many elements V₁, …, V_n of C and matching elements x₀, x₁, …, x_n such that x=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n=y.

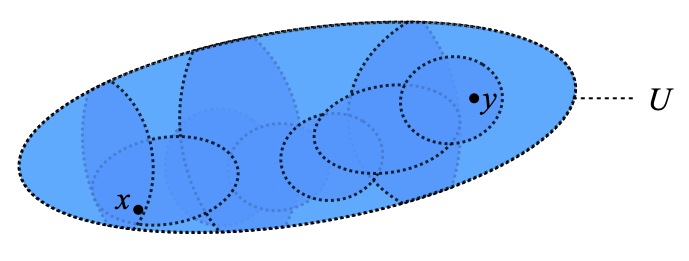
Last time, I used a picture like the following in order to illustrate the latter condition. We are given two points x and y in an open set U in blue, covered by a family C of open subsets of U, with dotted boundaries:

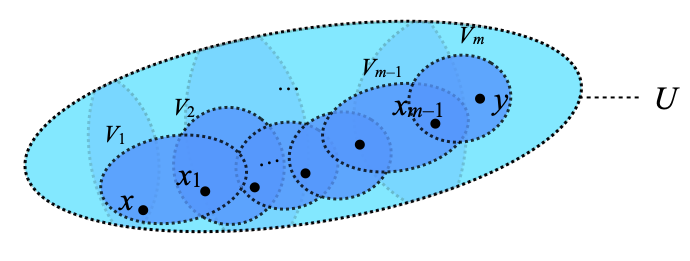
Then we can find a finite list of open subsets V₁, …, V_n in the cover C that are linked together as follows:

We can now make precise the statement that streams are to prestreams what sheaves are to presheaves.

Proposition A. Let (X, (⊑_U)_{U ∈ OX}) be a prestream.

• If it is a stream, then its presheaf of locally monotone maps with values in any poset P is a sheaf.
• Conversely, if its presheaf of locally monotone maps with values in S ≝ {0, 1}, ordered by 0<1, is a sheaf, then (X, (⊑_U)_{U ∈ OX}) is a stream.

Proof. For the first item, let U be an open subset of X, and C be an open cover of the subspace U. We assume we are given monotone maps f_V from V (with its local preordering ⊑_V) to P, for each V in C, such that f_V and f_W agree on V ∩ W for all V, W in C. (That is what the consistency condition of a sheaf says.)

There can be just one map f from U to P whose restriction to each V in C is equal to f_V, and it is defined by f(x)≝f_V(x) for every x in V. We only need to check that f is monotonic from U to P, where U is given the preordering ⊑_U. Hence, let x and y be any two points in U such that x ⊑_U y. By the definition of a circulation, there are finitely many elements V₁, …, V_n of C and matching elements x₀, x₁, …, x_n such that x=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n=y. Now x₀ and x₁ are both in V₁, and x₀ ⊑_V1 x₁, so f_V1(x₀)≤f_V1(x₁). By definition of f, f(x₀)≤f(x₁). Reasoning from the inequality x₁ ⊑_V2 x₂ instead, we obtain f(x₁)≤f(x₂), and so on, until f(x_n–1)≤f(x_n). Chaining all those inequalities together, we finally obtain that f(x)≤f(y).

For the second item, we assume that the presheaf of locally monotone maps with values in S is a sheaf. Let, once again, U be an open subset of X, and C be an open cover of the subspace U. Let also x and y be two points of U such that x ⊑_U y. For each V in C, we build a function f_V : V → S as follows. For every point z in V, we decide that f_V(z)≝1 if and only if there are finitely many elements V₁, …, V_n of C and matching elements x₀, x₁, …, x_n such that x=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n=z.

• For all points z and z’ of V, if f_V(z)≝1 and z ⊑_V z’, then we can extend the chain shown above to x=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n ⊑_V z’, showing that f_V(z‘)≝1; so f_V is monotonic from V to S.
• Given any other element W of C, for every z in V ∩ W, it is clear that f_V(z)=f_W(z): both sides of the equality are defined independently of V or W. Hence the family of maps f_V, V ∈ C, is consistent.
• By the sheaf property, there are all restrictions of a unique monotone map f from U to S, where U is equipped with the preordering ⊑_U. The important thing is that f is monotone with respect to ⊑_U, as we will see very soon.
• Also, f(x)=1 since f_V(x)=1, by definition of f_V, where V is any element of C such that x is in V. It suffices to take the trivial chain from x to x (n≝0, x₀≝x)
• Since f is monotone with respect to ⊑_U, f(y) is also equal to 1. Explicitly, this means that there are finitely many elements V₁, …, V_n of C and matching elements x₀, x₁, …, x_n such that x=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n=y.

This shows that (X, (⊑_U)_{U ∈ OX}) is a stream. ☐

When is the presheaf of locally monotone continuous maps of a prestream a sheaf?

We have a similar result with the presheaf of locally monotone continuous maps. However, the second part seems to require the following additional assumption on our presheaf. A binary relation R on a topological space is lower semicontinuous (or lsc, for short) if and only if the set of antecedents R^–1(U) ≝ {x | for some y in U, (x,y) is in R} of elements of U by R is open, for every open set U. Let me say that a precirculation (⊑_U)_{U ∈ OX} is lsc if and only if every local preordering ⊑_U is lsc on U, for every open subset U of X. A presheaf is lsc if and only if its precirculation is.

Proposition B. Let (X, (⊑_U)_{U ∈ OX}) be a prestream.

• If it is a stream, then its presheaf of locally monotone continuous maps with values in any poset P is a sheaf.
• Conversely, if (X, (⊑_U)_{U ∈ OX}) is lsc and if its presheaf of locally monotone continuous maps with values in Sierpiński space S ≝ {0, 1}, ordered by 0<1, is a sheaf, then (X, (⊑_U)_{U ∈ OX}) is a stream.

Proof. The proof of the first item is as above. We only need to check that the function f obtained by gluing the consistent family of locally monotone continuous maps f_V is not only monotone but continuous, and that is straightforward.

For the second item, the proof strategy is the same, but we need to replace the map f_V : V → S, which is monotone but not necessarily continuous, by another map f’_V : V → S. We define f’_V(z) as 1 if and only if, for every open neighborhood V’ of z included in V, there is an open neighborhood U’ of x such that, for every point x’ of U’, there are finitely many elements V₁, …, V_n of C and matching elements x₀, x₁, …, x_n such that x‘=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n and x_n is in V’. In other words, instead of requiring a chain of points from x to z, connected by open sets in the cover C, we require that starting from any point x’ that is closed enough to x, we can form a chain of points from x to a point that lies in an arbitrarily small open neighborhood V’ of z. The map f’_V is then continuous by construction, and f’_V(x)=1 (just take U’ equal to V’). The slightly tricky point is showing that f’_V is monotonic, and this is where we need the precirculation to be lsc. Explicitly, if f’_V(z)≝1 and z ⊑_V z’, then for every open neighborhood V” of z’, by the lsc property V’ ≝ ⊑_V^–1(V”) is an open neighborhood of z. By definition of f’_V, there is an open neighborhood U’ of x such that, for every point x’ of U’, there are finitely many elements V₁, …, V_n of C and matching elements x₀, x₁, …, x_n such that x‘=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n and x_n is in V’. Since V’ = ⊑_V^–1(V”), there is a point x_n+1 in V” such that x_n ⊑_V x_n+1. This allows us to extend the latter chain to x‘=x₀ ⊑_V1 x₁ ⊑_V2 … ⊑_Vn x_n ⊑_V x_n+1, with x_n+1 in V’‘, showing that f’_V(z’)≝1. ☐

Stalks

Earlier in this post, I said that, in a sense, every sheaf could be seen as a sheaf of (certain) locally continuous maps. I also said that I would not have time to explain the mathematics behind that result. However, I would like to set out the groundwork for that construction, and to give you an example of what this yields on some streams.

For each point x in X, we can form the stalk F_x of the presheaf at x. That is a kind of infinitesimally close view to the sets F_U as U becomes a smaller and smaller open neighborhood of x.

Categorically, F_x is the colimit of the diagram of those sets F_U and those restriction maps r_UV, where U and V are restricted to be open neighborhoods of x. (Even more abstractly, the colimit of the restriction of F to the full subcategory of OX^op consisting of open neighborhoods of x.)

Explicitly, one can check that F_x is built as follows.

• First, we build the disjoint union F[x] of the sets F_U, where U ranges over the open neighborhoods of x; its elements are pairs (U, f) where f ∈ F_U.
• We declare two elements (U, f) and (V, g) of F[x] to be equivalent, in notation (U, f) ≡_x (V, g), if and only if there is an open neighborhood W of x included in both U and V such that r_WU(f)=r_WV(g). (I will let you check that this is an equivalence relation.)
• F_x is the quotient F[x]/≡_x.

Let us look at the presheaf of locally monotone (resp., and continuous) maps from a prestream (X, (⊑_U)_{U ∈ OX}) to some fixed poset P. Then F[x] is the collection of pairs (U, f) where f is a monotone (resp., and continuous) map from some open neighborhood U of x to P. Let us be slightly less formal: F[x] is the collection of all monotone (resp., and continuous) maps from a open neighborhood of x (think: a small one) to P. And any two such monotone maps f and g are considered equivalent if and only if they coincide on an even smaller open neighborhood of x. Even less formally: we consider f and g to be equivalent if and only if f(x+dx)=g(x+dx) for every infinitesimally small value dx (whatever that may mean!). In other terms, an element of F_x is really just a value (of f at x) plus a “differential” df at x. Additionally, since we are working with (pre)streams and the local preordering is important, we only consider “positive” differentials, which exhibit a direction of movement that is forward in time.

The notion of “differential” here is very vague, of course. The locally monotone (resp., and continuous) maps I am considering here are far from being differentiable, even when the underlying topological space X is a manifold. Quite some time ago, Jimmie Lawson [2] studied manifolds with local directions of time, and if you have read that paper (or even just the beginning), you should recognize some very similar ideas, and notably the notion of cone fields; I may talk about that in another post, another time!

The stalks of the (sheaf of locally monotone maps on the) directed circle

One of my main examples of streams has constantly been the directed circle S₁^→ (pictured below): this is the space of complex numbers of modulus 1, namely the numbers of the form e^iθ, θ ∈ R, with the subspace topology induced by the inclusion in the complex plane; and x ⊑_U y holds if and only if we can write x as e^iθ, y as e^iθ’, with θ≤θ’, and such that for every t in the interval [θ, θ’], e^it is in U.

Let us consider the sheaf of locally monotone maps from S₁^→ to S, and let us compute its stalks. One should notice that a monotone map f from U to S is given equivalently by the upwards-closed f^–1({1}) (upwards-closed… with respect to ⊑_U). In the converse direction, we build a monotone map with codomain S by taking the characteristic function of an upwards-closed set. (In the case of the sheaf of locally monotone continuous maps, we only consider the upwards-closed open subsets of U.)

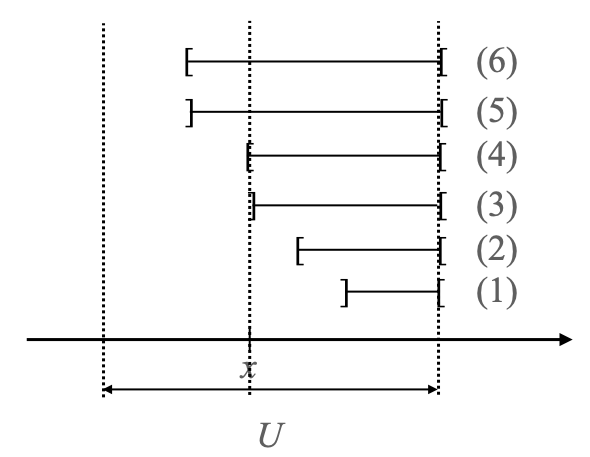
For sufficiently small open neighborhoods U around each point x of the directed circle, those upwards-closed subsets will just look like segments ]a, b[ or [a, b[ (plus the empty set). Let us examine several kinds of upwards-closed subsets of a sufficiently small open neighborhood U of x:

Of those, type (1) and (2) are equivalent: taking smaller and smaller open neighborhoods around U, you will eventually contain no point of intervals of type (1) or (2). (Namely, the corresponding characteristic maps of type (1) and type (2) vanish on sufficiently small open neighborhoods of x.) In fact, type (1), type (2), and the empty set are all equivalent with respect to ≡_x.

Then we find type (3), whose left endpoint is right at x, but does not contain x. That is an equivalence class of its own: whatever open neighborhood W of x, W will always intersect the type (3) interval, strictly to the right of x, but that interval does not contain x or any point to the left of x.

Similarly, type (4) is an equivalence class of its own: whatever open neighborhood W of x, W will intersect the type (4) interval at x and to its right, but not at any point strictly to the left of x.

Finally, type (5), type (6), and the whole of U are all equivalent: any sufficiently small open neighborhood of x will be completely included in any of them.

Hence the stalk F_x at any point x of S₁^→ contains just four points: “far-right” (equivalent to type (1) and (2)), “right-strict” (type (3)), “right-slack” (type (4)), and “anywhere” (type (5), type (6)).

In the case of the sheaf of locally monotone continuous maps to S, types (2), (4) and (6) do not occur. This simplifies the correspond stalks slightly, which in this case only contains three points, namely “far-right”, “right-strict”, and “anywhere”.

Before we continue, let us notice an additional property of the stalks F_x of the presheaf of locally monotone (resp., continuous) maps from a prestream to P. Let me write [f] for the equivalence class of a monotone (resp., and continuous) map f : U → P modulo ≡_x.

Fact. The stalks F_x of the presheaf of locally monotone (resp., and continuous) maps from a prestream to P, at any point x, are ordered, by [f] ≤_x [g] if and only if, for some sufficiently small open neighborhood W included in the domains of f and g, f_|W ≤ g_|W. (We order functions pointwise.)

The étale space of a (pre)sheaf

There is a fundamental construction, due to Alexander Grothendieck (as are a lot of things related to sheaves), of the étale space of a presheaf (X, F), where F is a functor from OX^op to Set. I will continue to write F_U for F(U), and r_UV : F_V → F_U for the usual restriction map (namely, r_UV is F applied to the inclusion map of U into V).

By the way, “étale” (pronounced ay-tahl, very approximately) is a corruption of the original word, which used to be “étalé” (ay-tahl-ay). In French, “étalé” means “spread out”, and indeed we are going to spread out the whole structure of the presheaf onto a much larger, new topological space. But “étale” means something else: “une mer étale” translates to “a slack sea”, and to a Frenchman such as me, an “étale space” has always sounded funny; I always seemed to picture it as a kind of large, calm ocean.

Anyway, here is the construction. The points of the étale space S(X, F) are those of the disjoint union of all the stalks F_x, where x ranges over the points of X. In other words, they are pairs (x, [f]), where x is a point in X and [f] is the equivalent class modulo ≡_x of an element f of a set F_U, where U is an open neighborhood of x. Notice that there is a projection map p : S(X, F) → X, which maps (x, [f]) to x.

One might think of defining the topology on S(X, F) as the coarsest one that makes p continuous, but that is not what we do. Instead, for every open subset U of X, for every f ∈ F_U, there is a map f : U → S(X, F) (overlined f) defined by f(x) ≝ (x, [f]) for every x in U — yes, that is quite a game with symbols! — and we declare the topology of S(X, F) to be the finest that makes all the underlined maps f continuous. The point is simply that we really want to consider any sheaf as a sheaf of locally-whatever (locally differentiable, locally monotone, etc.) continuous functions.

Explicitly, a subbase of the topology of S(X, F) is given by the subsets V of S(X, F) such that f^–1(V) is open (in U) for every open subset U of X and every f ∈ F_U.

It turns out that this makes the projection map p continuous, and a lot more than just that as well.

Lemma. We have the following.

1. For every open subset U of X, for every f ∈ F_U, the direct image f(U) is open in S(X, F).
2. The map p is continuous from S(X, F) to X.
3. The map p is a local homeomorphism: for every point (x, [f]) of S(X, F), there is an open neighborhood V of (x, [f]) such that p restricts to a homeomorphism of V onto some open neighborhood U of x.
4. The sets f(U), where U ranges over the open subsets of X, and f ranges over F_U, form a base of the topology of S(X, F).

Proof. 1. It suffices to show that g^–1(f(U)) is open for every open subset V of X and every g ∈ F_V. In order to do so, we pick any point x in g^–1(f(U)) (in particular, x is in V), and we will show that x has an open neighborhood entirely contained in g^–1(f(U)). By definition, since x is in g^–1(f(U)), g(x)=(x, [g]) is of the form (y, [f]) for some point y of U. In particular, x=y, and therefore x is both in V and in U. Moreover, f ≡_x g, so there is an open neighborhood W of x, included in both U and V, such that f and g have the same restriction to W; namely, r_WU(f)=r_WV(g).

This W is the open neighborhood we are looking for. For every point z in W, g(z)=(z, [g]) is also equal to (z, [f]) since f and g have the same restriction to W, an open neighborhood of z; and that is equal to f(z), which is therefore in f(U).

2. For every open subset U of X, p^–1(U) is the collection of elements (x, [f]) such that x is in U, and is therefore the union of all the sets f(U), where f ranges over F_U. All those sets are open by 1.

3. Given (x, [f]), where f is in F_U, we simply take V to be f(U). This is open by 1. Every element of V is of the form (y, [f]) for some unique y in U (with the same f). In other words, p is bijective from V onto U, with f as inverse. We have just shown that p is continuous, and we recall that f is continuous by definition of the topology on S(X, F).

4. Let us consider any open neighborhood W of any point (x, [f]) of S(X, F). By item 3, which we have just proved, (x, [f]) has an open neighborhood V = f(U) such that p restricts to a homeomorphism from V onto U, with inverse f. The image of V ∩ W by p is an open subset W of X included in U, and the restriction of the map f to W coincides with g, where g≝r_WU(f), simply because f and g have the same restriction to W in the sense that r_WU(f)=r_WW(g). Therefore V ∩ W is equal to g(W). The latter is therefore an open set (by item 1) of the desired form, containing x and included in W. ☐

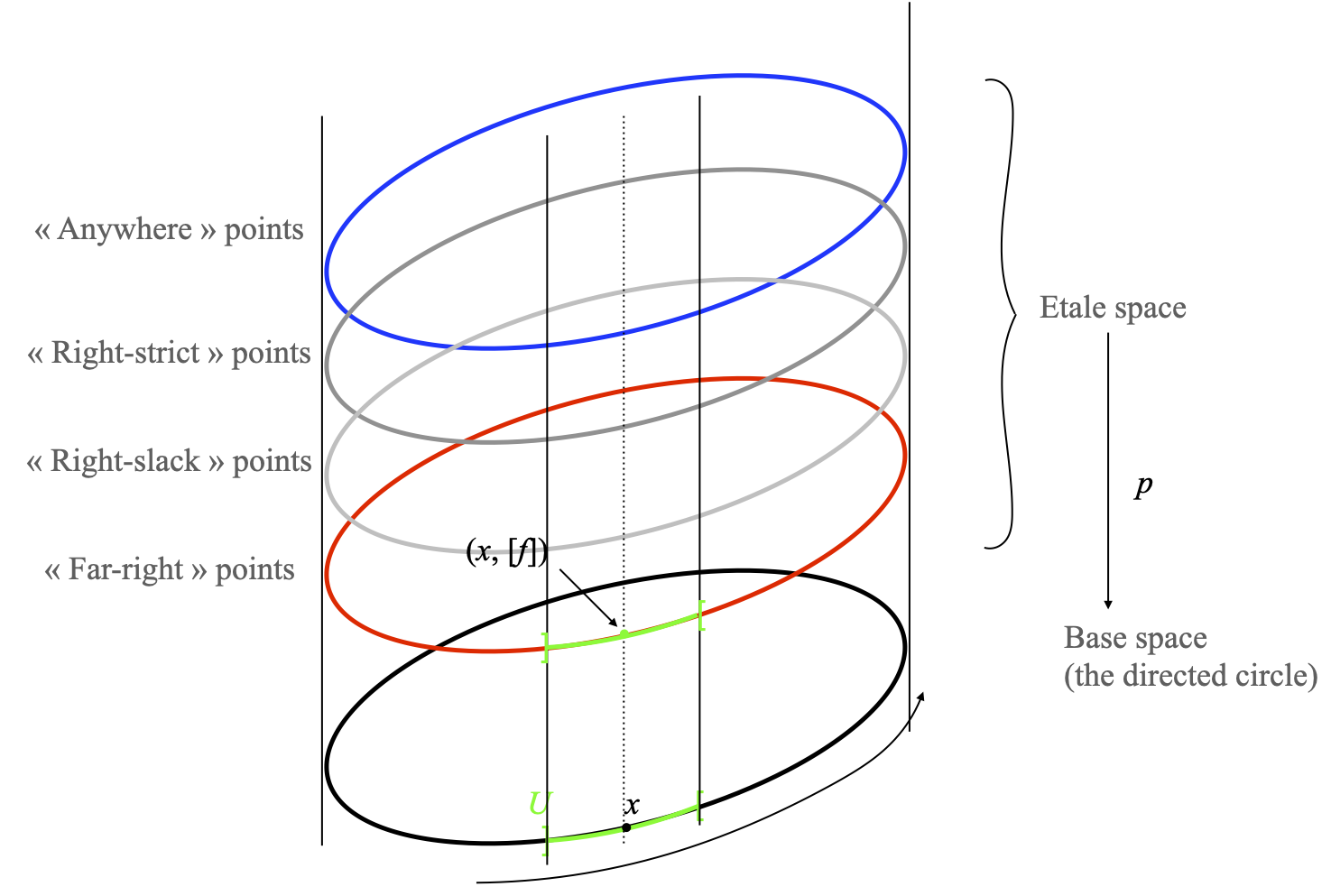
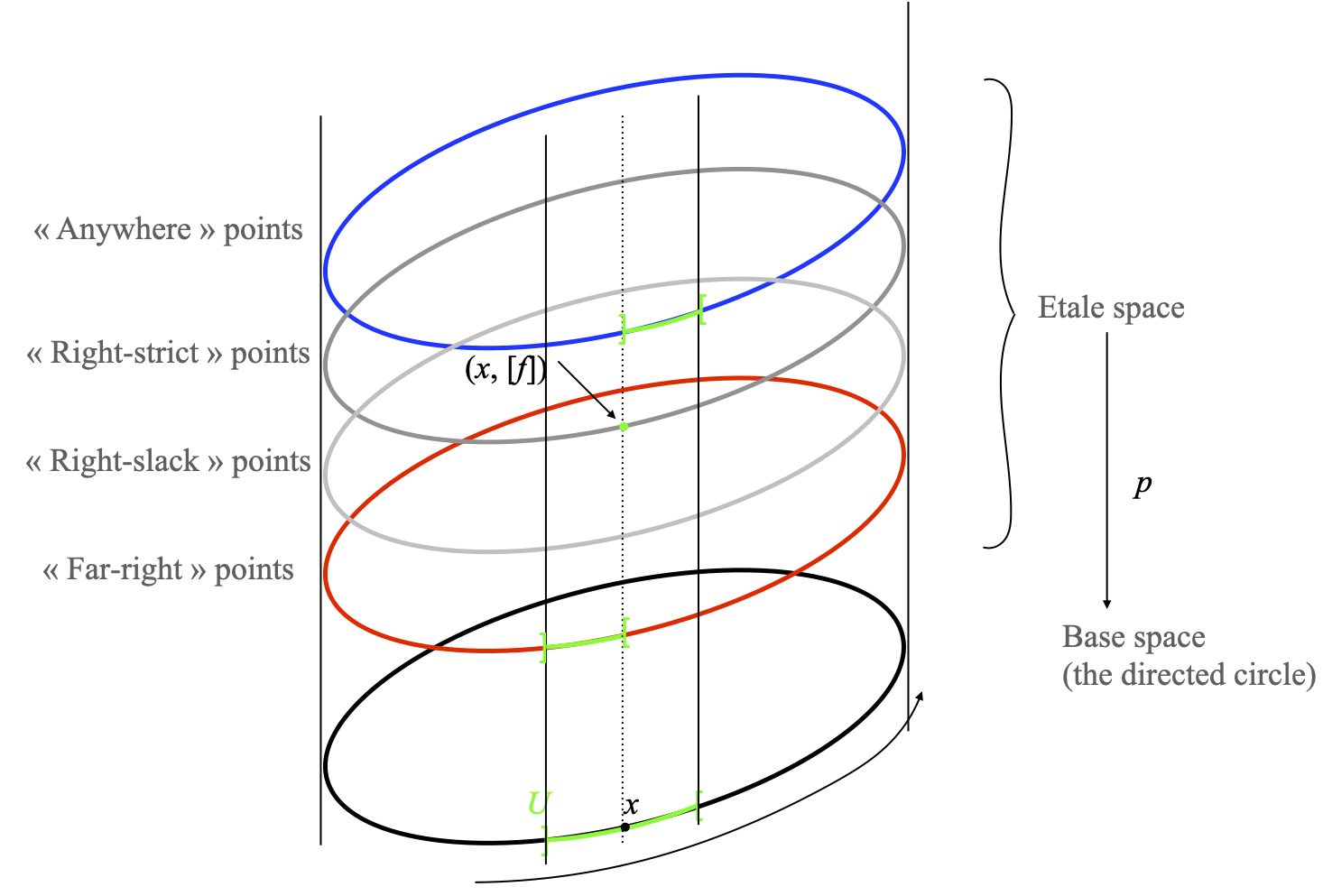
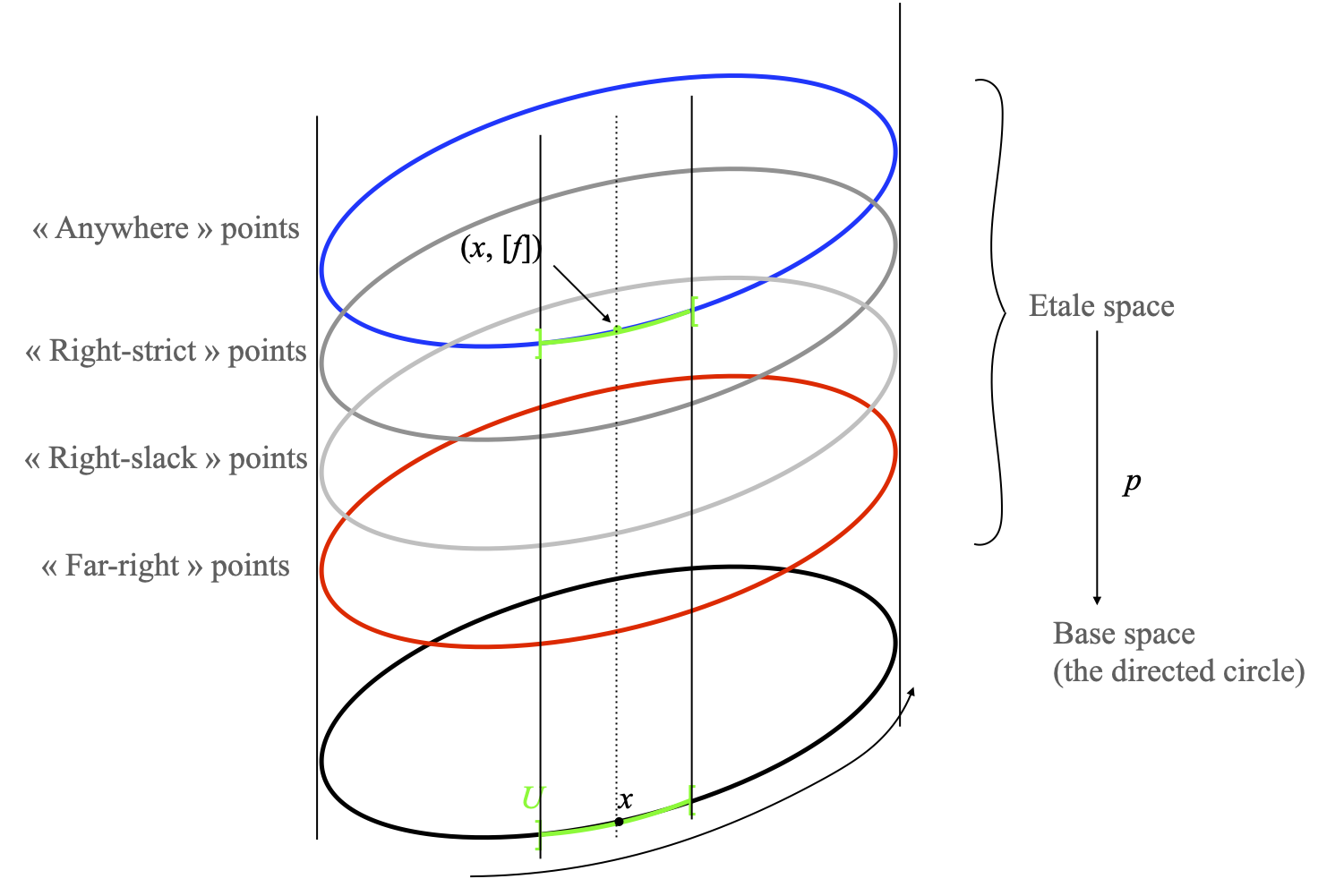
The étale space of the (sheaf of locally monotone maps on the) directed circle

Let us picture S(X, F) in the case of the sheaf of locally monotone maps from X to S. We recall that the stalk F_x at each point consists of four elements, which I have called “far-right”, “right-strict”, “right-slack”, and “anywhere”. F_x is also the set of antecedents of the point x by the projection map p, so S(X, F) just looks like a stack of four circles which all project down to the directed circle.

Now something must encode the local direction of time (the circulation) on the directed circle S₁^→ inside its étale space S(X, F) or its projection map p. And that is the topology on the étale space. As we will see, this is a pretty strange, non Hausdorff topology (although it is T₁, and locally Hausdorff, in the sense that every point has a Hausdorff neighborhood).

In order to understand the topology on the étale space of the directed circle, we use item 4 of the previous Lemma. Given any point x in the base space (the directed circle itself), there are four points (x, [f]) that project back to x through p. Correspondingly, we obtain four kinds of open neighborhoods f(U) of points of that form, one for each f. When f is of the “far-right” kind, namely when f : U → S is equal to 0 at x, to the left of x, and slightly to the right of x as well, then we obtain the open neighborhood shown in green below. Let me do the computation explicitly, but with loose notations. For U small enough, f is just equal to 0 on the whole of U. For every y in U, f(y)=(y, [f]) lies on the “far-right” layer:

Nothing weird yet. If f is of the “right-slack” kind, then f is equal to 0 strictly to the left of x, and to 1 at x and to its right. Hence, for every y in U, we have three cases for (y, [f]): if y is strictly to the left of x, then f will be equal to 0 both to the left and to the right of y, so (y, [f]) will be on the “far-right” layer; if y=x, then (y, [f]) will be on the “right-slack” layer; and if y lies strictly to the right of x, then f will be equal to 1 both a bit to the left and to the right of y, so (y, [f]) will be on the “anywhere” layer. This yields the following picture of our second kind of basic open set:

Observe how our new basic open set has a left part on the bottom layer, then an isolated point on the second layer from the bottom, then a right part on the top layer. The third kind of basic open set is obtained when (x, [f]) is of the “right-strict” kind. We obtain a basic open subset of the étale space of almost the same shape. The only change is that, when y=x, (y, [f]) is on the “right-strict” layer instead of the “right-slack” layer:

This is where we see how the local preorderings of the stream are encoded. Let me recall that the stalks F_x are ordered (by [f] ≤ [g] if and only if the locally monotone map f is pointwise below g on some sufficiently small open neighborhood of x). This ordering is the “from bottom to top” ordering in the pictures above, and the fact that the local preorderings on the directed circle turn along the curvy arrow shown at the bottom of the picture above are encoded by the fact that the latter two examples of basic open subsets “jump” from a lower to an upper layer when we travel in that direction.

Finally, when (x, [f]) is of the “anywhere” kind, then by choosing U small enough, f will be equal to 1 on the whole of U, and we obtain our fourth and final form of basic open subset in the étale space, lying entirely in the “anywhere” layer:

We can play exactly the same game with the sheaf of locally monotone continuous maps from the directed circle to S. The only change is that S(X, F) would now have only three, not four, circles stacked onto each other: there would be no “right-slack” layer at all.

Next time

Let me stop there. The construction of the étale space of a presheaf, and in particular that of the sheaf of locally monotone (resp., and continuous) maps from a stream to S, should be enough for one post! Next time, I plan to explain the fundamental equivalence between sheaves on X and local homeomorphisms onto X. That is not new, but I hope to illustrate the constructions with prestreams and streams once again, and that should be new.

1. Saunders MacLane and Ieke Moerdijk. Sheaves in geometry and logic. A first introduction to topos theory. Springer Science+Business Media New York (Universitext), 1992.
2. Jimmie D. Lawson. Ordered manifolds, invariant cone fields, and semigroups. Forum Mathematicum 1.3:273-308, 1989.

— Jean Goubault-Larrecq (November 22nd, 2021)