Last time, I had introduced two models of directed topological spaces, namely of topological spaces with a local direction of time:
- Marco Grandis’ d-spaces [1], which are pairs (X, dX) of a topological space and of a collection dX of paths (namely, continuous maps from [0,1] to X), the so-called d-paths, that contains all the constant maps, and is closed under concatenation and reparametrization;
- Sanjeevi Krishnan’s prestreams [2], which are pairs (X, (⊑U)U ∈ OX) of a topological space X and a precirculation (⊑U)U ∈ OX, namely a collection of preorderings ⊑U on U, one for each open subset U of X, with a monotonicity property: if U ⊆ V, then for all points x, y of U such that x ⊑U y, we also have x ⊑V y. (Oops, I had not mentioned the name “precirculation” last time; so yes, we are going to call those collections of preorderings precirculations, and there will be things called circulations below.)
I would like to explain how S. Krishnan’s notion of stream emerges naturally from the relation between the two notions. I initially had plans for explaining much more that what I am going to say below, but I am just returning from holidays, and I have not been able to devote the usual 3 to 4 days that it usually takes me to write one of my (now monthly) blog posts. There is some good in any evil, as one says, and this will allow me to concentrate on just one topic, instead of trying to attack too many questions at once.
Streams
The real subject of [2] is not prestreams, rather streams, which I will talk about today. Perhaps the simplest way of introducing them is to recall Emmanuel Haucourt’s S ⊣ D adjunction [3], and to find new properties of those prestreams produced by applying the S functor to an arbitrary d-space.
The situation is similar with the O functor from Top to the opposite of the category CLat of complete lattices, mapping every topological space to its complete lattice of open sets. Soon enough we realize that all such lattices obey the so-called frame distributivity law. We call such lattices frames, and we realize that they are interesting in their own right. Not all frames are obtained by applying O to a topological space. Similarly, the interesting property we will find of prestreams obtained by applying S to a prestream will turn them into so-called streams. This will be an interesting notion in its own right, although not all streams are obtained by applying S to a d-space.
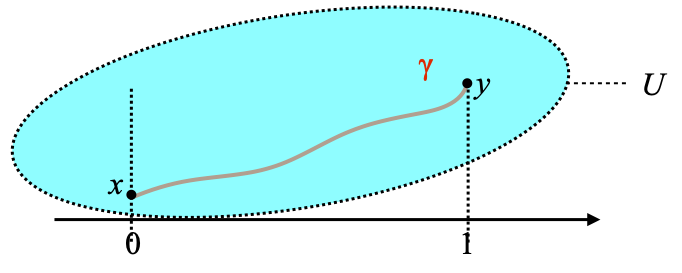
All right, so how does S work? Given a d-space (X, dX), we decide to define S(X, dX) as (X, (⊑U)U ∈ OX), where for every open subset U of X, as the following preordering on U: x ⊑U y if and only if there is a d-path γ from x to y (i.e., γ(0)=x and γ(1)=y), whose image Im γ is entirely included in U.
Fact. Let (X, (⊑U)U ∈ OX) ≝ S(X, dX). Then (⊑U)U ∈ OX is a circulation, namely: for every open subset U of X, for every open cover C of the subspace U (namely, each V ∈ C is open in X and included in U), ⊑U coincides with the “join” of the preorderings ⊑V, V ∈ C, in the sense that:
for all points x, y in U, x ⊑U y if and only if there are finitely many elements V1, …, Vn of C and matching elements x0, x1, …, xn such that x=x0 ⊑V1 x1 ⊑V2 … ⊑Vn xn=y.
The latter formulation implicitly entails that x0 and x1 are both in V1, x1 and x2 are both in V2, …, xn–1 and xn are both in Vn. I will explain what this “join” is, really, later.
Proof. This is a consequence of the compactness of [0,1], really, plus a certain form of connectedness. Let me recall that we equip [0,1] with its usual Hausdorff topology; not with its Scott topology, for example.
The if direction is trivial: if x=x0 ⊑V1 x1 ⊑V2 … ⊑Vn xn=y, we must have x=x0 ⊑U x1 ⊑U … ⊑U xn=y.
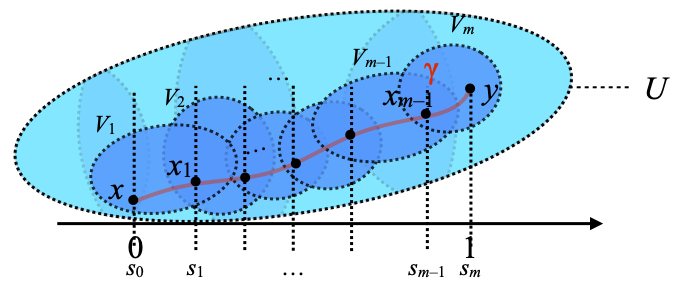
Conversely, we use the fact that (X, (⊑U)U ∈ OX) is equal to S(X, dX): hence there is a d-path γ : [0,1] → X such that γ(0)=x, γ(1)=y, and Im γ ⊆ U. The situation is as follows:
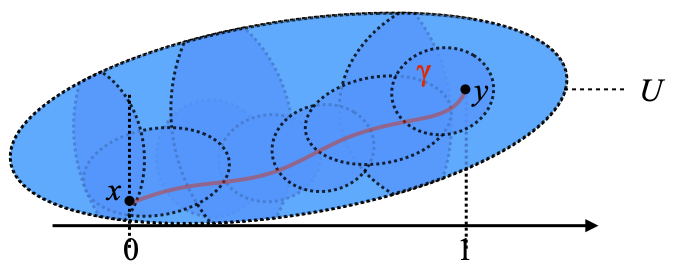
Also, U = ∪C, so U really is a union of open subsets, which we display as the following collection of darker blue potato shapes; each one is an open set V from the cover C.
Then γ–1(U) = ∪V ∈ C γ–1(V), and therefore the sets γ–1(V), V ∈ C, form an open cover of [0,1].
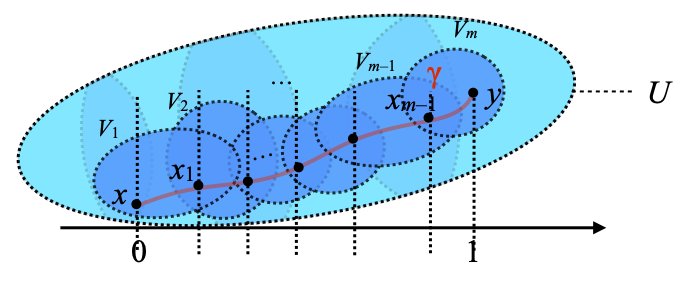
The desired sets V1, …, Vn are obtained by extracting a finite subcover of that open cover of [0,1], as you may guess. In pictures, here is what we are looking for:
Let us get on with the technical details.
A base of the topology of [0,1] is given by what I will call open intervals: those are the intersections of actual open intervals of R with [0,1], hence are sets of the form ]a,b[ with 0≤a<b≤1, and also sets of the form [0,b[ with 0<b≤1, and ]a,1] with 0≤a<1.
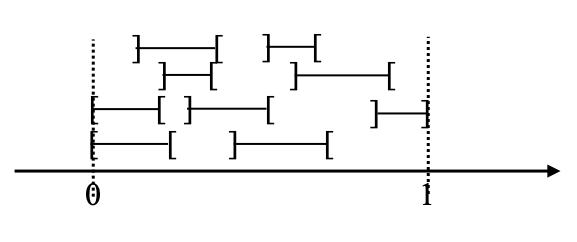
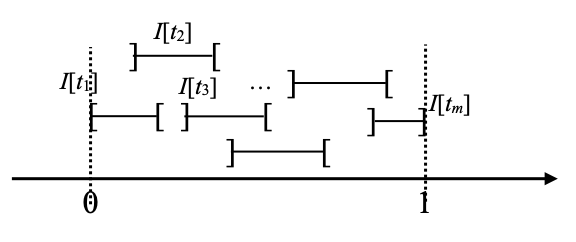
For each t ∈ [0,1], t is in γ–1(V) for some V ∈ C, and since γ–1(V) is open, t must be contained in some open interval I[t] contained in that set γ–1(V). The open sets I[t], t ∈ [0,1], themselves form an open cover of [0,1], and we extract a finite subcover I[t1], …, I[tm]. Here is how this finite subcover, consisting of open intervals, may look like.
We massage the latter list in order to ensure that none of the latter intervals contains any other, by removing any I[tj] that is included in some I[tk], for some k≠j, iteratively. For example, there are two intervals containing 0 in the picture above, and we keep only the larger of the two. In pictures, we obtain the following.
The result is a list of pairwise incomparable intervals, with respect to inclusion. We can then sort this list from left to right. This means that the left endpoint of I[t1] is smaller than or equal to the left endpoint of I[t2], which is smaller than or equal to the left endpoint of I[t3], etc., and similarly for right endpoints. This is how we sorted them in the picture above. Formally, this rests on the following observation: given any two intervals with endpoints a,b and c,d respectively that are incomparable with respect to inclusion, either a≤c and b≤d, or a≥c and b≥d, namely comparing them by left endpoints a,c gives the same result as comparing them by right endpoints b,d.
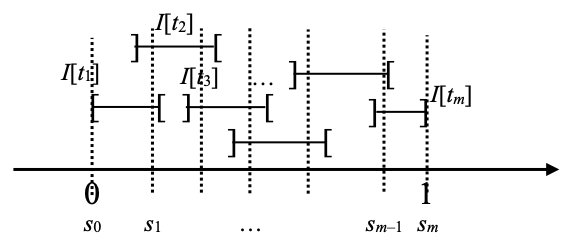
For each j with 1≤j≤m, let aj be the left endpoint of I[tj] and let bj be its right endpoint. Since 0≤a1≤a2≤…≤am≤1, and since I[t1], …, I[tm] cover [0,1], we must have a1=0. Similarly, bm=1. Also, successive intervals I[tj] and I[tj+1] must overlap: otherwise no point in the open interval ]bj,aj+1[ would belong to any I[tk]: those with k≤j cover only points that lie to the left of bj, and those with k≥j+1 cover only points that lie to the right of aj+1. Since they overlap, we pick an element sj in I[tj] and I[tj+1], for each j such that 1≤j≤m–1. Let us also define s0 be 0, and sm be 1. The situation is now as follows.
Let us look at the list of elements 0=s0≤s1≤s2≤…≤sm=1. It is easy to check that [s0,s1] is included in I[t1], [s1,s2] is included in I[t2], …, [sm–1,sm] is included in I[tm]. We define n as m+1, and the open subsets V1, …, Vn of U as follows. For each j, 1≤j≤n=m+1, [sj–1,sj] is included in I[tj], and the latter is included in an open set γ–1(V) for some V ∈ C: we let Vj be any such V. The situation is now as follows.
We now let xj ≝ γ(sj) for each j, 0≤j≤n. For each j with 1≤j≤n, γ has an obvious subpath from xj–1 to xj, which one obtains by reparametrization. In particular, that subpath is a d-path. Since [sj–1,sj] ⊆ I[tj] ⊆ γ–1(Vj), the image of that subpath is entirely included in Vj. Therefore xj–1 ⊑Vj xj. ☐
A prestream (X, (⊑U)U ∈ OX) whose precirculation (⊑U)U ∈ OX is a circulation (namely satisfies the condition of the above Fact) is called a stream.
A few examples, a few non-examples
- Recall the directed circle, defined as the following prestream S1→: this is the space of complex numbers of modulus 1, namely the numbers of the form eiθ, θ ∈ R, with the subspace topology induced by the inclusion in C, as in the d-space case.
For every open subset U, for all x, y in U, x ⊑U y holds if and only if we can write x as eiθ, y as eiθ’, with θ≤θ’, and such that for every t in the interval [θ, θ’], eit is in U. We had seen last time that this is a Haucourt stream, namely the image by the functor S of a certain d-space. As such, S1→ is a stream. In fact, every Haucourt stream is a stream. - The directed line segment I→ is a Haucourt stream, hence a stream. Let me recall that its (pre)circulation is defined as follows: for every open subset U of [0,1], for all x, y in U, x ⊑U y if and only if x≤y and the whole segment [x,y] is included in U.
- Every topological space X equipped with a preordering ≤ defines a prestream by declaring that ⊑U is the restriction of ≤ to U for every open subset U of X. This is almost never a stream. For that, you would need the circulation property to hold, namely “for every open subset U of X, for every open cover C of the subspace U, for all points x, y in U, if x ≤ y then there are finitely many elements V1, …, Vn of C and matching elements x0, x1, …, xn such that x=x0 ≤ x1 ≤ … ≤ xn=y, and each pair xi–1, xi lies in Vi“. (Do not forget the last part of the condition: when we say that xi–1 is below xi in the restriction of ≤ to Vi, this really means that not only xi–1 ≤ xi, but also that both xi–1 and xi are in Vi.)
For example, this condition fails if you take [0,1] for X, and its usual ordering for ≤: let U be the disjoint union of [0, 1/3[ and ]2/3, 1], x be 0, and y be 1, and let the cover consist of just the two open sets [0, 1/3[ and ]2/3, 1]. Imagine that you could find V1, …, Vn in the cover and elements x0, x1, …, xn as above. (By the way, we only have two sets in that cover, but the list V1, …, Vn can, and will usually, contain repeated copies of those two sets; I never insisted that V1, …, Vn be distinct open sets, right?) Now x=x0 is in [0, 1/3[ and not in ]2/3, 1], so V1 must be [0, 1/3[. Next, the pair x0, x1 lies in V1, so x1 is also in [0, 1/3[. Then the pair x1, x2 lies in V1, so x2 is also in [0, 1/3[. Continuing in the same way, we realize that every xi must be in [0, 1/3[. This is in particular true for xn=y=1, which is absurd. - Every topological space can be given the discrete precirculation, where ⊑U is the trivial preordering on U that makes every point below any other point. This is a special case of a preordered topological space (see previous bulleted item), where the preordering is the trivial one.
By a similar argument as above, the discrete precirculation cannot be a circulation if X contains a disconnected open set U, in other words if U can be written as a disjoint union of two non-empty open subsets. This rules out a lot of topological spaces! However, if X has a top element ⊤ in its specialization preordering, then the discrete precirculation is a circulation: given any two points x and y of an open set U, and an open cover C of the subspace U, we pick one element V1 from C that contains x, one element V2 from C that contains y, and we realize that x ⊑V1 ⊤ ⊑V2 y (recall that ⊑V1 and ⊑V2 are both trivial), that the pair x, ⊤ lies in V1, and that the pair ⊤, y lies in V2. - Every topological space can be given the indiscrete precirculation, where ⊑U is just equality. This is again a preordered topological space, with equality as preordering. This one is always a circulation: if x ⊑U y, then in fact x=y, and from there the circulation property is trivial.
A lattice-theoretic view
Earlier, I mentioned that a precirculation (⊑U)U ∈ OX is a circulation if ⊑U coincides with the “join” of the preorderings ⊑V, V ∈ C, for every open subset U of X and every open cover C of the subspace U. I also promised that I would explain the term “join”.
The typical view is that this condition is equivalent to requiring that the preordered set (U, ⊑U) be the colimit (up to isomorphism), taken in the category of preordered sets and monotonic maps, of the diagram of preordered sets (V, ⊑V), where V ranges over the open subsets of U, and with the obvious inclusions as morphisms. (I am saying that out of memory, and I have not checked it again, so please excuse me if that is incorrect.) Hence “join” means colimit.
This is a nice observation, and one that leads to the view of streams as cosheaves, which is most certainly how S. Krishnan came to invent them [2].
However, this view misses an important point, and one that will stare you in the face if you ever try to design a Stone duality theory for streams (something I planned to do, but that I have not completed yet): the points of the preordered set at index U ∈ OX should be the points of U itself (up to isomorphism). We are not defining precirculations as any old diagram of preordered sets indexed by the open subsets U of X; the set of points in those preordered sets must be the set of points of the index U itself. This is a pretty strong requirement, really.
I cannot resist mentioning another formulation of prestreams and streams, which I have not seen in the literature, and which avoids this pitfall entirely.
Let call a modified prestream any pair (X, (⊑’U)U ∈ OX) of a topological space X, and of a family of preorderings ⊑’U on X (not on U! this is the main modification) for each open subset U of X such that:
- the usual monotonicity condition holds: if x ⊑’U y and U is included in V, then x ⊑’V y;
- for each open subset U of X, ⊑’U is supported on U, namely: for all points x ⊑’U y in X, x and y are both in U or x=y. This may be clearer if I state that in the equivalent way: for all distinct points x ⊑’U y, x and y must be in U; or, equivalently again: for all points x ⊑’U y, if x or y is not in U then x=y.
Given any prestream (X, (⊑U)U ∈ OX), we can define an associated modified prestream (X, (⊑’U)U ∈ OX) by letting x ⊑’U y hold if and only if either both x and y are in U and x ⊑U y, or x=y is not in U. (⊑’U is the modification of ⊑U.) Conversely, given any modified prestream (X, (⊑’U)U ∈ OX), we obtain a prestream (X, (⊑U)U ∈ OX) by declaring that ⊑U is the restricting of ⊑’U to U, for each open subset U of X. The two constructions are inverse of each other.
There is a category PreStr’ of modified prestreams, whose morphisms f : (X, (⊑’U)U ∈ OX) → (Y, (⪯’V)V ∈ OY) are the continuous maps f from X to Y that are monotonic from the preordered set (X, ⊑’U) to (Y, ⪯’V), where U and V range over the pairs of open subsets such that U=f–1(V). (Yes, that means an infinite number of monotonicity conditions.)
It is easy to see that PreStr and PreStr’ are equivalent categories—in fact isomorphic categories; we have just described the natural isomorphism between the two categories.
Now there is yet another formulation of modified prestreams. There is a complete lattice of preorderings Pre(X) on the set X. The lattice structure is as follows. Preorderings are compared by inclusion: ⊑’ is included in ⪯’ if and only if for all points x and y such that x ⊑’ y, we also have ⪯’. Then infima are just intersections: x is below y with respect to the infimum of a family of preorderings if and only if x is below y with respect to each of the preorderings in the family. And since we have all infima, we have all suprema, too: the supremum of a family is the infimum of its set of upper bounds.
One can check that, explicitly, the supremum ⊑’ of a family of preorderings (⊑’i)i ∈ I on X is given by x ⊑’ y if and only if there are finitely many indices i1, …, in in I, and a matching sequence of points x=x0 ⊑i1 x1 ⊑i2 … ⊑in xn=y. (I guess you can see the connection with circulations emerge now.)
For every (open, although that is not essential) subset U of X, there is a largest preordering ⊑’0U on X that is supported on U. This is the preordering that declares x to be below y if and only if either both x and y are in U (without any further condition on U), or x=y. This defines a map dX from OX to Pre(X), which sends U to ⊑’0U. (“d” is for “discrete”.) This map is monotonic, and a preordering ⊑’ on X is supported on U if and only if ⊑’ is included in dX(U)=⊑’0U.
Hence a modified prestream is, equivalently, a pair of a topological space X and of a monotonic map U ↦ ⊑’U from OX to Pre(X) that is (pointwise) below the map dX. In other words, it is a pair (X, circ) where circ is an element of ↓dX, the downward closure of dX in the complete lattice of monotonic maps from OX to Pre(X). Through the isomorphism between PreStr and PreStr’, such elements of ↓dX are exactly the precirculations on X.
Now what is a circulation? That it is simply an element of ↓dX that preserves all suprema (up to the isomorphism between unmodified and modified precirculations).
Indeed, one can characterize circulations without relying on covers in the following way: a precirculation (⊑U)U ∈ OX on X is a circulation if and only if for every family C of open subsets of X, letting U≝sup C (the union of all the elements of C), ⊑U is the preordering on X defined by the fact that for all points x, y in U, x ⊑U y if and only if there are finitely many elements V1, …, Vn of C and matching elements x0, x1, …, xn such that x=x0 ⊑V1 x1 ⊑V2 … ⊑Vn xn=y. Relying on the explicit characterization of suprema in Pre(X) that I gave above, you will see that this means that the modification ⊑’U of ⊑U is required to be the supremum of the modifications ⊑’V of the preorderings ⊑V, V ∈ C.
In other words:
A (modified) stream is a pair (X, circ) where circ is an element of the complete lattice of supremum preserving maps from OX to Pre(X), below dX.
(In passing, beware that dX itself is not in general supremum preserving. The argument is exactly the same as the one that we used to show that the discrete precirculation on [0,1] is not a circulation.)
I was somehow hoping that this observation would perhaps lead to a nice theory of Stone duality for streams. One would consider general frames L (instead of OX) together with a supremum preserving map from L to some localic stand-in for ↓dX ⊆ Pre(X). The latter is the problem: in general, Pre(X) is very far from being a frame! In fact, it is in general not even distributive, as I will let you check for yourselves.
Well, another time, maybe.
The category of streams
There is a full subcategory Str of prestreams that consists of streams. Its morphisms are exactly the stream morphisms, namely the continuous, locally monotonic maps.
The adjunction S ⊣ D restricts to one between the category dTop of d-spaces and Str: by definition, S maps into Str.
One can show that Str is complete, cocomplete, and that colimits are computed exactly as in the larger category PreStr of prestreams. Hence in particular, the directed circle S1→ is also a quotient of the directed line segment I→ in Str, where by quotient I mean the relevant coequalizer, if that does not frighten you.
Limits are very different. One can show that Str is a coflective subcategory of PreStr, namely that the inclusion functor (of PreStr into Str) has a right adjoint (see [2], or Corollary 3 in [4]). This right adjoint is called cosheafification.
Intuitively, the cosheafification of a prestream (X, (⊑U)U ∈ OX) is obtained as follows.
- We first replace each preordering ⊑U by a new one ^⊑U (the hat ^ is written above ⊑ in [4], but this is hard to render in html), defined so as to repair the circulation condition. Namely, we define x ^⊑U y, for all points x and y of an arbitrary open set U as: for every open cover C of the subspace U, there are finitely many elements V1, …, Vn of C and matching elements x0, x1, …, xn such that x=x0 ⊑V1 x1 ⊑V2 … ⊑Vn xn=y.
The resulting family (^⊑U)U ∈ OX is another precirculation on X, and one such that x ^⊑U y implies x ⊑U y (take the open cover consisting of the sole set U). Let me call the new prestream (X, (^⊑U)U ∈ OX) the one-step cosheafification of (X, (⊑U)U ∈ OX). - The one-step cosheafification of (X, (⊑U)U ∈ OX) may fail to be a stream, so we iterate the process… transfinitely. The process stops at some ordinal, and what we obtain is the cosheafification of (X, (⊑U)U ∈ OX). Put in a simpler, albeit more abstract way, there is a complete lattice of precirculations on X, and one-step cosheafification defines a monotonic, deflationary operator on that complete lattice; cosheafification finds the largest fixed point of that operator below the initial precirculation ⊑U.
The lattice-theoretic view that we have seen earlier makes this easier to grasp, perhaps. We start with a (modified) precirculation circ, namely a monotonic map circ from OX to Pre(X), and below dX. The cosheafification is obtained by replacing circ by the largest supremum preserving map below circ. This can also be obtained by as the largest fixed point of some one-step cosheafification process. It is easier to realize that there is always a largest supremum preserving map below any map f, which one obtains as the pointwise supremum of the family of all supremum preserving maps below f. Indeed, any pointwise supremum of supremum preserving maps is itself supremum preserving.
As in the care of any coflective subcategory, limits in Str are obtained by applying the coreflection functor (cosheafification) to limits computed in the larger category PreStr. A nice things is that, in the case of products, cosheafification stabilizes at step 1: in other words, the product of two streams in Str is the one-step cosheafification of their product in PreStr [4, Proposition 12].
Sheaves
Why is the cosheafification called cosheafification? Well, simply because streams are cosheaves of preordered sets. In other words, the circulation condition really means that, for a prestream (X, (⊑U)U ∈ OX) to be a stream, each preordered set (U, ⊑U) must be the colimit, taken in the category of preordered sets and monotonic maps, of the diagram of preordered sets (V, ⊑V), where V ranges over the open subsets of U, and with the obvious inclusions as morphisms.
But talking about (co)sheaves would lead me too far away for now, so I’ll talk about them another time!
- Marco Grandis. Directed Algebraic Topology: Models of Non-Reversible Worlds. New Mathematical Monographs 13, Cambridge University Press, 2009. ISBN-13 978-0-521-76036-2.
- Sanjeevi Krishnan. A convenient category of locally preordered spaces. Applied Categorical Structures, 17(5):445–466, 2009.
- Emmanuel Haucourt. Streams, d-spaces, and their fundamental categories. Electronic Notes in Theoretical Computer Science 283, pages 111–151, 2012.
- Jean Goubault-Larrecq. Exponentiable streams and prestreams. Applied Categorical Structures 22, pages 515–549, 2014. The published version, available from Springer Link, contains two mistakes, which are repaired in the HAL report.

— Jean Goubault-Larrecq (August 24th, 2021)