Aliaume Lopez’ master theorem of Noetherian spaces

First of all, Season’s Greetings!

Second, I would like to mention that this blog has now been in existence for 10 years now, too. The first post dates from November 5th, 2012, and was a succinct summary of Matthew de Brecht’s quasi-Polish spaces. Another reason to celebrate!

But enough talking; let us get to today’s topic.

In the theory of any kind of spaces, it is useful to have ways of constructing spaces. For example, you may want to know that products of bc-domains, that spaces of Scott-continuous functions between bc-domains, all are bc-domains.

In the case of Noetherian spaces, I have given a few constructions in Section 9.7 of the book: the Hoare hyperspace of a Noetherian space is Noetherian, finite products and finite coproducts of Noetherian spaces are Noetherian, the space of finite words over a Noetherian alphabet is Noetherian, the space of finite trees over a Noetherian signature is Noetherian, etc. All of them are proved in pretty different ways, and one may wonder whether there would be some kind of master theorem that would include all, or at least most, of the constructions at once.

For the purpose of this post, let me say (or remind you) that a space X is Noetherian if and only if every monotone sequence of open sets (U_n)_{n ∈ N} stabilizes, namely: there is an index n₀ such that all the sets U_n with n≥n₀ are equal. Equivalently, X is Noetherian if and only if every open subset of X is compact. I will also say that a topology τ on a set X is Noetherian if and only if the space (X, τ) is Noetherian.

What Aliaume Lopez achieved

Aliaume Lopez proved such a theorem this year [1]. He found his proof by scrutinizing the proof of Theorem 9.7.46 in the book (the topological Kruskal theorem, on finite trees), and distilling its essence. The result is pretty remarkable. There have been pretty similar theorems for well-quasi-orders [2,3], and Aliaume shows how Ryu Hasegawa’s construction [2], for one, is a consequence of his theorem; his construction goes further, not just because it applies to the larger class of Noetherian spaces, but also because it shows the Noetherianity of spaces that are not obtained as initial constructions, contrarily to [2,3].

What he does is as follows. Imagine you start with some Noetherian topology on a set X, and that you have an operator E that maps Noetherian topologies on X to Noetherian topologies. Now iterate E, possibly transfinitely, and take the topology generated by the union of all the iterates. This gives you a new topology, which I will call the limit topology of E. When is that limit topology Noetherian?

(Oh, before you ask: that limit topology has nothing to do with categorical limits or colimits, in any sense that I know of.)

Aliaume discovered that the crucial property that is needed in order to achieve this is that E should be what he calls a topology expander. This is defined by a few conditions. The first one is pretty innocuous: E should be monotonic, in other words, it should map finer Noetherian topologies to finer Noetherian topologies. The important condition is pretty mysterious, and I will come back to it later.

Oh well, I am lying slightly, too. Aliaume considers maps E from all topologies to topologies, which the proviso that E respects Noetherianness. But we do not need to define E on non-Noetherian topologies.

Meanwhile, let us consider an example. This is also the example that Aliaume uses to motivate the construction [1, Definition 3.9, Lemma 3.10]. I modified it slightly; the result is a bit simpler in my view.

The example of words

Let me say, or recall, how the word topology on the set X* of finite words on Noetherian space X is constructed (see Definition 9.7.26 in the book).

The elements of X* are the words over the alphabet X. Let us call a subword of a word w any word obtained as a not necessarily contiguous subsequence of the letters of w. For example, cde is a subword of abcdefg, but bdeg is a subword as well. (This is not the word embedding preordering ≤* defined after Definition 9.7.26 in the book. Aliaume uses ≤*, but we will obtain similar results with the simpler notion of subwords.) For a more complicated example involving several occurrences of the same variable, aab is a subword of acacbc.

The word topology on X* has a base of open sets of the form X*U₁X*…X*U_nX*, where U₁, …, U_n are arbitrary open subsets of X. Another way of writing these basic open sets is as ⬆U₁…U_n, where:

• U₁…U_n is the set of words a₁…a_n, where each a_i is a letter in U_i;
• for every subset W of X*, I will write ⬆W for the set of words that have a subword in W; namely, the set of words such that, by removing enough occurrences of letters, we eventually obtain a word in W.

The word topology can be obtained as the limit topology of an operator E, starting from the indiscrete topology: for every topology τ on X*, E(τ) is the topology generated by the sets ⬆UW, where U ranges over the open subsets of X and W ∈ τ. (UW is the set of words aw with a ∈ U and w ∈ W, namely those which start with a letter in U, and whose remaining letters form a word in W.)

In order to see that the limit topology of E, starting with the indiscrete topology τ₀ on X*, is the word topology, we proceed as follows.

• The only open subsets of τ₀ are the empty set and X* itself.
• τ₁≝E(τ₀) is the topology with subbasic open sets ⬆UX*, where U is open in X: those sets are the sets X*UX* of words that contain a letter in U.
• τ₂≝E(τ₁) is the topology with subbasic open sets ⬆UX* and ⬆UX*VX*, where U and V are open in X, namely X*UX* and X*UX*VX*.
• In general, the mth iterate τ_m is generated by the open sets X*U₁X*…X*U_nX* where n≤m. Then the limit topology is the union of all those, and that is simply the word topology.

Now, it is pretty easy to check that E maps Noetherian topologies to Noetherian topologies. In order to show this, we use the version of Alexander’s subbase lemma that is suited to Noetherian spaces: a topological space Y, with a subbase B, is Noetherian if and only if every sequence (B_n)_{n ∈ N} of elements of B is good, meaning that there is an index n such that B_n ⊆ ∪_i<n B_i. (The hard direction is the bad sequence lemma, namely Lemma 9.7.15, in the book. The other direction is by definition.) Let τ be a Noetherian topology on X. Then a subbase B of the topology E(τ) is given by the sets ⬆UW with U open in X and W ∈ τ. We consider a sequence (⬆U_nW_n)_{n ∈ N} of elements of B. The sequence (U_n × W_n)_{n ∈ N} is a sequence of open sets in the topological product of X and (X*, τ), and the product of two Noetherian spaces is Noetherian (Proposition 9.7.18 (vii) in the book). Hence there is an index n such that U_n × W_n ⊆ ∪_i<n (U_i × W_i), and then it is immediate that ⬆U_nW_n ⊆ ∪_i<n ⬆U_iW_i. This argument is similar to Lemma 3.12 in [1], although Aliaume uses a different operator E.

Aliaume’s master theorem will imply that X* with the subword topology is Noetherian (under the assumption that X is Noetherian, which is what we assumed from the beginning).

In the book, showing that the subword topology is Noetherian is done by a special construction based on minimal bad sequences (Theorem 9.7.26); Aliaume’s master theorem saves you from doing that. Of course, it is itself proved using a minimal bad sequence argument.

The topology τ/V

The crucial condition in the definition of topology expanders is a pretty strange one, and Aliaume and I took ages to convince ourselves that it was somehow a natural condition. It does not resemble anything I know in topology, and it has no natural categorical explanation either, as far as I can see.

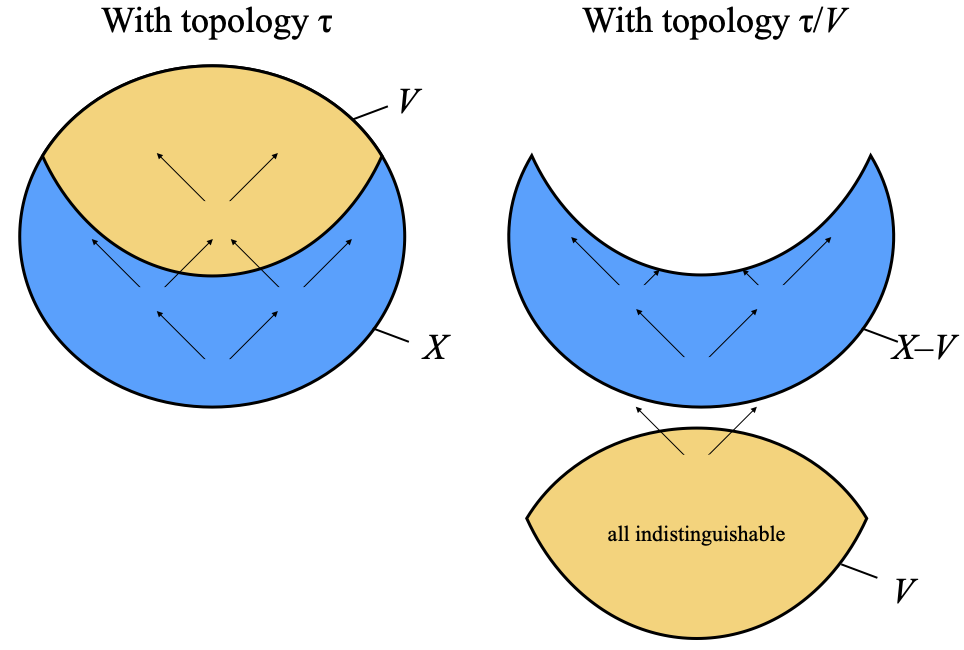
I will define that condition in a slightly different form as Aliaume, in order to only speak about open sets, not closed sets. (The topology τ/V below is what Aliaume writes as τ|C, where C is the complement of V.) We consider a Noetherian topology τ on X, and an element V of τ. From this, we can form a funny topology:

Definition. For every V ∈ τ, the topology τ/V is the topology with a base given by the sets U–V, where U ranges over τ.

The topology τ/V localizes τ with respect to V, in the sense that it makes one big lump of indistinguishable points out of all the points in V, where I consider two points to be indistinguishable if they belong to the same open sets, namely if they are both below and above each other in the specialization preordering. Also, it moves that big lump below all the remaining points. This is best understood by looking at the following picture, where V is shown in orange, and the arrows are indicative of ways of moving up in the specialization preordering.

Formally, let ≤/V be the specialization preordering of X under the topology τ/V, and ≤ be that of X under τ: x ≤/V y if and only if, for every U ∈ τ, x ∈ U/V implies y ∈ U/V. If x is in V, then this is always true, so every point of V is below any point whatsoever with respect to ≤/V. More generally, we have x ≤/V y if and only if x is in V, or both x and y are outside V and x≤y.

We note the following. In particular, given an operator E that takes a Noetherian topology as input, that means that if E(τ) makes sense, then E(τ/V) also makes sense.

Note. If τ is Noetherian, then so is τ/V.

Proof. Let us consider any monotone sequence U_n–V of elements of τ/V, n ∈ N. Then the sets U_n ∪ V are equal to (U_n–V) ∪ V, and therefore form a monotone sequence of elements of τ. If τ is Noetherian, there is an index n₀ such that all the sets U_n ∪ V with n≥n₀ are equal. Then all the sets U_n–V = (U_n ∪ V) – V are also equal for n≥n₀, so τ/V is Noetherian. ☐

Taking set differences of open sets, and making a topology out of them, is a pretty rarely used operation in topology, but not an unusual one. That is an important operation in the proof of the topological Kruskal theorem (theorem 9.7.46 in the book), and more specifically in the construction of Lemma 9.7.45. This should come as no surprise, as that is the proof that Aliaume took as a starting point of his generalization. Beyond that specific argument, the Skula topology of a topology τ, which has a base of set differences U–V, where both U and V range over τ; and look! It turns out that a space (X,τ) is Noetherian if and only if X is compact in the Skula topology of τ, by R.-E. Hoffmann’s theorem (exercise 9.7.16 in the book). Hence using set differences of open sets should not be frowned upon too much in this context. Of course, τ/V is not the Skula topology of τ, since V is fixed. But there is perhaps something deeper to be obtained by comparing the τ/V construction with the Skula topology.

Topology expanders

Now, given a Noetherian topology τ, we can compute E(τ), and we can also compute E(τ/V), since we have noticed that τ/V is also Noetherian. The crucial condition that Aliaume requires is almost the fact that E(τ)=E(τ/V) for every V ∈ τ, or rather that E(τ) is indistinguishable from E(τ/V) modulo the operation that localizes by V, namely that E(τ/V)/V = E(τ)/V.

In fact, he only needs the inclusion E(τ)/V ⊆ E(τ/V)/V, and only for those Noetherian topologies τ such that τ ⊆ E(τ), because those are the only topologies that are required in the proof. (This also saves us from assuming that τ ⊆ E(τ) for every topology τ on X.) Let us put that into a formal definition.

Definition. A topology expander on a set X is a monotonic map E from Noetherian topologies on X to Noetherian topologies on X such that:

1. for every Noetherian topology τ on X such that τ ⊆ E(τ), for every V ∈ τ, E(τ)/V ⊆ E(τ/V)/V.

Explicitly, condition 1 means:

• for every Noetherian topology τ on X such that τ ⊆ E(τ),
• for every V ∈ τ,
• for every set W in E(τ), W–V can also be written as W’–V for some W’ in E(τ/V).

In other words, we only need to apply E to the localization τ/V instead of τ itself in order to obtain the same set W–V. I will use the following criterion below; that is an easy verification.

Fact A. In order to check condition 1, it is enough to verify the above, not for all sets W in E(τ), but for the sets W taken from any given subbase of E(τ). In other words, let us imagine that E(τ) is generated by some subbase B. Then condition 1 for a Noetherian topology τ (such that τ ⊆ E(τ)),is equivalent to:

• for every V ∈ τ,
• for every set W in B, W–V can also be written as W’–V for some W’ in E(τ/V).

Here is (finally!) the master theorem.

Theorem [1, Theorem 3.21]. Let E be a topology expander on a set X, and τ₀ be a Noetherian topology on X such that τ₀ ⊆ E(τ₀). Then E has a least fixed point above τ₀ in the poset of Noetherian topologies. Explicitly, one can define finer and finer topologies τ_α on X by induction on the ordinal α, by:

• τ₀ is already defined;
• τ_α+1≝E(τ_α) for every ordinal α;
• τ_α is the topology generated by all the topologies τ_β, β<α, when α is a limit ordinal.

The topologies τ_α are all Noetherian, they form an ascending chain, and the least fixed point of E above τ₀ is obtained as τ_α, where α is the first ordinal such that τ_α+1=τ_α, necessarily a non-limit ordinal.

I will give the argument—in fact a slightly adapted argument that proves a bit more—in the Appendix. The argument is pretty technical, and this post is already long enough without it.

An example of a topology expander: the case of words

In the meantime, it is interesting to see why the operator E we took as an example for constructing the word topology on X* is a topology expander.

Let me recall that, for that operator, E(τ) is generated by the sets ⬆UW, where U ranges over the open subsets of X and W ∈ τ. In order to check that E is a topology expander, we assume a Noetherian topology τ such that τ ⊆ E(τ).

• We first observe that every set V in τ must be upwards closed in the subword ordering, namely that for every word w in V that occurs as a subword of some word w’, then w’ is also in V. Indeed, since τ ⊆ E(τ), V is also in E(τ), hence is a union of finite intersections of sets of the form ⬆UW, which are all upwards closed in the subword ordering, by construction.
• Now we use Fact A (see above). We take any element ⬆UW of the subbase defining E(τ), an element V of τ, and we claim that (⬆UW)–V can be written as some element of E(τ/V) minus V. It is entirely unimportant what the exact shape of V is: the important thing is that V is upwards closed in the subword ordering, as we have just argued.
  Let W’≝W–V: this is in τ/V by definition. Then we form ⬆UW’, which is in E(τ/V), and we claim that (⬆UW)–V = (⬆UW’)–V. Since W’ is included in W, (⬆UW’)–V is included in (⬆UW)–V. In the other direction, let us consider any word w in (⬆UW)–V. One can write w as …a…w’…, where a is in U, w’ is in W, and the ellipses “…” denote parts of the word of lesser importance. Now w’ is a subword of w: if w’ were in V, then w would be in V, too, so w’ is not in V; this is where we use that V is upwards closed in the subword ordering. Therefore w’ is in W–V, namely, in W’. As a consequence, w = …a…w’… is in ⬆UW’. By assumption, w is not in V, so w is in (⬆UW’)–V.

A non-expander

In order to understand a notion, it is useful to have not just examples of the notion, but also counterexamples. Aliaume and I discussed the following minimal counterexample last Thursday (December 15th, 2022). Let X be Z^– ∪ {–∞}, the set of non-positive integers 0, –1, –2, …, with an additional element –∞ added below all others.

We define a monotonic function F from Noetherian topologies on X to Noetherian topologies on X by letting F(τ) be the topology generated by the sets (U–1) ∪ {0}, where U ranges over τ; I am writing U–1 for {x–1 | x ∈ U}.

Starting from the indiscrete topology on X, the successive iterates of F will produce {0}, then {0, –1}, then {0, –1, –2}, etc., as successive new open sets. The limit topology, namely the topology generated by the union of all those collections of open sets, is the Alexandroff topology of X, with its obvious ordering. That topology is not Noetherian, because the ascending sequence of open sets {0}, {0, –1}, {0, –1, –2}, …, is not stationary.

Hence F cannot be a topology expander. What is failing? Well, let τ be the topology whose open sets are ∅, {0}, {0, –1}, {0, –1, –2}, and X itself. This is the second (or third) iterate of F; nothing special, really, and you could have taken any of the other iterates. Let V be {0, –1, –2}. Then τ/V consists of ∅, {–3, –4, …, –∞}=X–V, and X. Let W be {0, –1, –2, –3}.

• W is in F(τ), because it is equal to (V–1) ∪ {0};
• so W–V = {–3} is in F(τ)/V.
• The elements of F(τ/V) are {0}, {0, –4, –5, …, –∞}, X… plus the empty set;
• so the elements of F(τ/V)/V are ∅, {–4, –5, …, –∞}, and {–3, –4, …, –∞}, plus X.
  As you may realize, W–V = {–3} is not in that list.

Other applications

Returning to the example of the topology expander E we have used to rederive the word topology, we retrieve the topological Higman lemma: if X is Noetherian, then X* is also Noetherian, in the word topology. That is not really a big deal: that result was not too hard to prove by elementary means.

More interestingly, Aliaume shows that his master theorem also implies the topological Kruskal theorem. The latter has a much more intricate proof, so that is perhaps a more interesting application. The proof using the master theorem relies on a topology expander that is very close in spirit to the one I have used for words. Let T(X) be the set of finite trees (a.k.a., terms) with vertices labeled by elements of X. For every open subset U of X, and for every subset W of T(X)*, let U〈W〉 denote the set of terms of the form f(t₁,…,t_n) such that f is in U and the word t₁…t_n (in T(X)*) is in W. Let ⬆U〈W〉 denote the set of terms that have a subterm in U〈W〉. Now the function that maps any Noetherian topology τ to the topology generated by sets of the form ⬆U〈W〉, where U is open in X and W is open in the word topology on (T(X), τ), is a topology expander. The argument is entirely similar to the one I have used on words above.

The master theorem can also be used to show that certain spaces of infinitary data structures are Noetherian. For example, I had proved, together with Simon Halfon and Aliaume Lopez, that there is a natural way of topologizing the set X^<α of transfinite words of length <α (for any ordinal α that is either indecomposable or the successor of an indecomposable ordinal) over a Noetherian space X, such that X^<α is Noetherian. This now comes out of Aliaume’s master theorem almost for free; at least without any more effort than for the case of finite words.

Finally, this gives new results as well. Aliaume mentions the case of ordinal-branching, infinite trees with finite branches (Section 4.3 in [1]): if X is Noetherian, then the space of those kinds of trees with vertices labeled by X is Noetherian, too. Similarly, we can now imagine that all sorts of infinitary tree-like structures will be Noetherian as well: ordinal-branching trees with ordinal long branches, finitary or infinitary 2-trees (namely, trees in which vertices have trees instead of lists of successors), 3-trees (with 2-trees as successors), and so on.

1. Aliaume Lopez. Fixed Points and Noetherian Topologies. arXiv report 2207.07614, October 2022.
2. Ryu Hasegawa. Two applications of analytic functors. Theoretical Computer Science, 272
   (1):113–175, 2002. doi:10.1016/S0304-3975(00)00349-2.
3. Anton Freund. From Kruskal’s Theorem to Friedman’s gap condition. Mathematical Struc-
   tures in Computer Science, 30(8):952–975, 2020. doi:10.1017/S0960129520000298.
4. Jean Goubault-Larrecq, Simon Halfon, and Aliaume Lopez. Infinitary Noetherian Constructions II. Transfinite Words and the Regular Subword Topology. arXiv report 2202.05047, February 2022.

— Jean Goubault-Larrecq (November 19th, 2022)

Appendix: proving the master theorem

Although Aliaume proves it for Noetherian topologies on a set X, the proof of the master theorem really has nothing to do with points. One might think that it is a locale-theoretic proof, but it is not, either. That is a purely order-theoretic proof, and I will explain it in this way.

Instead of considering set differences, taken in P(X) for some set X, one can replace P(X) by a complete Boolean algebra S. Using a coframe instead would be enough to obtain a suitable analogue of set differences, but the next ingredient requires that it should be a frame, too. Instead of topologies τ, we work with subframes of S, namely with subsets of S that are closed under finite infima and arbitrary suprema. (The frame distributivity law is automatically inherited from S.)

Then I realized that the proof also worked if we take for S a Boolean algebra, not necessarily a complete one. In that case, since we no longer have infinite suprema, τ should vary among the sub-(bounded lattices), namely the subsets that are closed under finite infima and finite suprema.

I had a hint that maybe S only needed to be a co-Heyting algebra in the latter case, but that makes some details of the proof too complicated or perhaps even false. The point is that a co-Heyting algebra, namely a poset whose opposite is a Heyting algebra, has a natural notion of subtraction.

A final case where the proof I will give will work is when S is a subtractive semilattice, namely, a sup-semilattice with a subtraction operation such that for all u, v, w in S,

(*) u–v ≤ w if and only if u ≤ v ⋁ w.

(In general, I will write ⋁ for supremum, ⋀ for infimum, ⊤ for the top element, and ⊥ for the bottom element, if they exist.) In the case of subtractive semilattices, τ will have to vary among the subsemilattices of S, namely the subsets that are closed under binary suprema. By the way, every subtractive semilattice must have a least element ⊥. Indeed, pick any element u of S. Then, for every element w of S, u–u ≤ w if and only if u ≤ u ⋁ w, which is trivially true: so u–u is the desired least element.

None of these cases seems to subsume any of the others, and I have not found a neat way of saying what they have in common. Hence I will simply treat all three cases in parallel.

In summary, in the following we will assume that S is a universe and τ varies among the loci inside S, where those terms are defined in one of the following possible ways:

• universe = complete Boolean algebra, locus = subframe, or:
• universe = Boolean algebra, locus = sub-(bounded lattice), or:
• universe = subtractive semilattice, locus = subsemilattice.

The main technique difference will be the notion of locus generated by a family A. This will be the smallest locus containing A, and will differ depending on which notion of locus we take.

A sequence (u_n)_{n ∈ N} of elements of a sup-semilattice is good if and only if there is an index n such that u_n ≤ ⋁_i<n u_i; it is bad otherwise. Let us say that a sup-semilattice is good if and only if all its sequences are good. A topology is good, as a sup-semilattice of open sets, if and only if it is Noetherian. (Hence it would seem reasonable to call sup-semilattices where all sequences are good Noetherian; but Noetherian in that context usually means well-founded instead.)

Given a locus τ included in the universe S, and an element v of S, we form the set τ/v of all elements of the form u–v, where u ranges over τ. Whatever our notion of universe, S is a subtractive semilattice, so that makes sense.

Lemma. For every locus τ inside S, for every v in S, τ/v is also a locus inside S. If τ is good, so is τ/v.

Proof. For the first part, this is clear when S is a (possibly complete) Boolean algebra. When it is merely a subtractive semilattice, we observe that (u₁–v) ⋁ (u₂–v) is equal to (u₁ ⋁ u₂)–v: it suffices to show that they have the same upper bounds, and indeed, (u₁ ⋁ u₂)–v ≤ w iff u₁ ⋁ u₂ ≤ v ⋁ w, iff u₁ ≤ v ⋁ w and u₂ ≤ v ⋁ w, iff (u₁–v) ≤ w and (u₂–v) ≤ w, iff (u₁–v) ⋁ (u₂–v) ≤ w. Therefore τ/v is a subsemilattice of S.

For the second part, let τ be good, and let (u_n–v)_{n ∈ N} be any sequence in τ/v. Since τ is good, there is an index n such that u_n ≤ ⋁_i<n u_i. For each i, we have u_i ≤ (u_i–v) ⋁ v (since that is simply equivalent to (u_i–v) ≤ (u_i–v)), so u_n ≤ ⋁_i<n ((u_i–v) ⋁ v) = (⋁_i<n (u_i–v)) ⋁ v. Therefore u_n–v ≤ ⋁_i<n (u_i–v). ☐

Let us call expander on S any monotonic map E from the set of loci to itself such that:

1. for every good locus τ inside S such that τ ⊆ E(τ), for every v in τ, E(τ)/v ⊆ E(τ/v)/v.

We fix an expander E on S, and a good locus τ₀ inside S such that τ₀ ⊆ E(τ₀). We define an ordinal-indexed sequence of loci τ_α inside S by induction on the ordinal α, by:

1. τ₀ is already defined;
2. τ_α+1≝E(τ_α) for every ordinal α, provided that τ_α is defined and good;
3. τ_α is the locus generated by the union of the loci τ_β, β<α, when α is a limit ordinal, provided that they are all defined and form an ascending sequence of loci.

In principle, some of the loci τ_α may fail to be good, so that τ_α+1≝E(τ_α) may fail to be defined in clause 2 above. This is the reason of the precaution I am taking by saying “provided that τ_α is defined” and the like. We will see that all the loci τ_α are actually well-defined, and good.

I will leave you the task of showing that if all the loci τ_β with β<α are well-defined, then they form an ascending sequence, for every ordinal α. This is due to our assumption τ₀ ⊆ E(τ₀), then to monotonicity of E, using transfinite induction.

In the next few results, I will assume a limit ordinal α such that every τ_β with β<α is a well-defined, good locus inside S, and that they form an ascending sequence of loci; I will also define τ_α as the locus generated by their union, as in clause 3 above.

The description of τ_α is pretty simple. If loci are defined as subsemilattices or as sub-(bounded lattices), then ∪_β<α τ_β is already a locus, so τ_α = ∪_β<α τ_β. If loci are defined as subframes, then the elements of τ_α are the unions of elements of ∪_β<α τ_β. In any case, the union ∪_β<α τ_β is a subsemilattice of S, and the following holds. (Note, JGL, Dec. 20th, 2022. The case of subframes, as posted on Dec. 19th, 2022, was incomplete. The fix involved adding the following lemma, and replacing τ_α by ∪_β<α τ_β almost everywhere in subsequent arguments.)

Lemma (bad sequence lemma). If τ_α has a bad sequence, then ∪_β<α τ_β has a bad sequence, too.

Proof. Only the case where loci are subframes needs a proof. We show the contrapositive: we assume that every sequence in ∪_β<α τ_β is good, and we will show that every sequence in τ_α must be good, too. To this end, we will simply show that τ_α=∪_β<α τ_β. Now let us imagine that this equality fails. Then we can find an element u in τ_α–∪_β<α τ_β. We can write u as a supremum of a family F of elements of ∪_β<α τ_β, by definition of τ_α. The family F is non-empty, otherwise u would be equal to ⊥, which is in ∪_β<α τ_β; so let us pick an arbitrary element u₀ from F. We note that u₀ is in ∪_β<α τ_β, so u₀ < u. There must be an element u₁ of F such that u₀ ⋁ u₁ is strictly larger than u₀, otherwise u₀ would be the supremum of F, and that would imply u=u₀, which is impossible. Next, there must be an element u₂ of F such that u₀ ⋁ u₁ ⋁ u₂ is strictly larger than u₀ ⋁ u₁, otherwise u₀ ⋁ u₁ would be the supremum of F, namely u₀ ⋁ u₁ = u; but each of u₀ and u₁ is in some τ_β with β<α, so u₀ ⋁ u₁ is also in some τ_β with β<α, and u is not. We continue in the same way, finding elements u_n in F in such a way that the sequence (u₀ ⋁ … ⋁ u_n)_{n ∈ N} is a strictly increasing of elements of ∪_β<α τ_β. However, since by assumption every sequence in ∪_β<α τ_β is good, we reach a contradiction. Hence there is simply no term u in τ_α–∪_β<α τ_β. It follows that τ_α=∪_β<α τ_β, and therefore that every sequence in τ_α is good. ☐

Every element u of ∪_β<α τ_β then occurs in τ_β for some β<α, and we can choose that β to be minimal, since the ordering relation on ordinals is well-founded. I will call that minimal β the depth of u (in ∪_β<α τ_β), and I will write it as d(u). We note that d(u) cannot be a limit ordinal (because no new element is added to τ_α that did not already exist in τ_β for some β<α). We can compare elements of ∪_β<α τ_β by their depths, and I will call this the depth ordering: this is a strict ordering where u is (strictly) less than v if and only if d(u)<d(v).

A minimal bad sequence in τ_α is a bad sequence (u_n)_{n ∈ N} in ∪_β<α τ_β that is minimal with respect to the lexicographic extension of the depth ordering; in other words, any lexicographically smaller sequence, necessary of the form u₀, u₁, …, u_n–1, v, … where v has strictly smaller depth than u_n, must be good.

Lemma (minimal bad sequence lemma). If ∪_β<α τ_β has a bad sequence, then it has a minimal bad sequence.

Proof. First, among any non-empty set of elements of ∪_β<α τ_β, we can always find one of minimal depth, because the ordering on ordinals is well-founded. Let u₀ be a minimal element of ∪_β<α τ_β that starts some bad sequence. Fixing u₀, let u₁ be a element of ∪_β<α τ_β of minimal depth such that there is a bad sequence beginning with u₀ and u₁. In general, once we have fixed u₀, u₁, …, u_k so that those start some bad sequence Σ_k, we let u_k+1 be any element of ∪_β<α τ_β of minimal depth such that u₀, u₁, …, u_k, u_k+1 starts some bad sequence Σ_k+1. Let Σ be the sequence u₀, u₁, …, u_k, … If it were good, then we would have u_n ≤ ⋁_i<n u_i for some n ∈ N, and therefore Σ_n would be good. Therefore Σ is bad. By construction, Σ is minimal bad. ☐

We will need to massage bad sequences slightly, and to this end, we use the following.

Lemma (massaging lemma). For every bad sequence (u_n)_{n ∈ N} in ∪_β<α τ_β:

1. every infinite subsequence is bad;
2. for every β < α, there are only finitely many elements u_n at depth β;
3. there is a strictly monotonic map ρ: N → N such that for all m,n ∈ N such that n < ρ(m), d(u_n) < d(u_ρ(m)).

Proof. Item 1 is clear. If item 2 failed, then we could extract an infinite subsequence of (u_n)_{n ∈ N} consisting of elements all at depth β. By item 1, that subsequence would be bad. This is impossible since τ_β is good. As far as item 3 is concerned, we define ρ(m) by induction on m. Let ρ(0)≝0. Assuming we have already defined ρ(0), . . . , ρ(m), there are only finitely many indices n such that d(u_n)=0 or d(u_n)=1 or … or d(u_n)=m. Hence there is an index n such that d(u_n) > m, and we define ρ(m+1) as the least one. ☐

The difficult, central piece of the argument is the following.

Proposition. Let α be a limit ordinal, and let us assume that every τ_β with β<α is a well-defined, good locus inside S, and that they form an ascending sequence of loci. Then τ_α is good.

Proof. This will take quite some time. We assume that τ_α is not good, and we aim for a contradiction. By the bad sequence lemma and the minimal bad sequence lemma, ∪_β<α τ_β has a minimal bad sequence (u_n)_{n ∈ N}.

Let us write Down(u_n) for the subsemilattice of all elements of depth strictly smaller than d(u_n); this is just a τ_β for some β<α, so Down(u_n) is good by assumption.

For every n≥1, let u_<n denote u₀ ⋁ … ⋁ u_n–1. We let τ’ be the locus generated by the union of all the loci Down(u_n)/u_<n, where n≥1. In other words, the elements of τ’ consists of the suprema of finite non-empty families of elements in ∪_n≥1 Down(u_n)/u_<n (in case a locus is a subsemilattice; when loci are sub-(bounded lattices), we need to take finite suprema of finite infima; when loci are subframes, we need to take arbitrary suprema of finite infima). We claim:

Claim. τ’ is good.

Instead of proving the claim, let us proceed with the proof. We will prove the claim later.

Let d_n ≝ d(u_n) for every n ∈ N. The sequence (d_n)_n∈N is monotonic: otherwise, let m be the smallest natural number such that d_m > d_m+1, then the sequence obtained from (u_n)_{n ∈ N} by removing its mth entry u_m would still be bad, by item 1 of the massaging lemma, and would be strictly smaller in the lexicographic extension of the depth ordering.

Let ρ be the strictly monotonic map given in item 3 of the massaging lemma. Let us fix an arbitrary m≥1. We have defined ρ in such a way that d(u_n) < d(u_ρ(m)) for every n<m; hence d(u_<ρ(m)), which is the maximum of the depths of the (finitely many) elements u_n, n<m, is also strictly smaller than d(u_ρ(m)). In other words, d(u_<ρ(m))<d(u_ρ(m)), and this means that u_<ρ(m) is in Down(u_ρ(m)).

Since E is an expander, we have E(Down(u_ρ(m)))/u_<ρ(m) ⊆ E(Down(u_ρ(m))/u_<ρ(m))/u_<ρ(m), and the latter is included in E(τ’)/u_<ρ(m) by monotonicity.

We recall that the depth d(u_i) cannot be a limit ordinal, for any i. Since m≥1, and since ρ is monotonic, ρ(m)>ρ(0), and therefore d(u_ρ(m)) is a limit ordinal that is different from 0, hence is a successor ordinal β+1. By definition of depth, u_ρ(m) must therefore be in E(τ_β), namely in E(Down(u_ρ(m))). Then u_ρ(m)–u_<ρ(m) is in E(Down(u_ρ(m)))/u_<ρ(m), and therefore, as we have seen above, in E(τ’)/u_<ρ(m). Hence we can write u_ρ(m)–u_<ρ(m) as v_m–u_<ρ(m), for some v_m ∈ E(τ’).

This holds for every m≥1. Using the Claim, the sequence (v_m)_m≥1 is good. Therefore v_m ≤ ⋁_1≤i<m v_i for some m≥1. Then u_ρ(m)–u_<ρ(m) = v_m–u_<ρ(m):

• is less than or equal to (⋁_1≤i<m v_i) – u_<ρ(m),
• which is equal to ⋁_1≤i<m (v_i – u_<ρ(m)) (because suprema in E(Down(u_ρ(m)))/u_<ρ(m) are computed as in E(Down(u_ρ(m))), namely as in S),
• which is less than or equal to ⋁_1≤i<m (v_i – u_<ρ(i)) (because ρ is monotonic),
• which is equal to ⋁_1≤i<m (u_ρ(i) – u_<ρ(i)) (by definition of v_i),
• which is less than or equal to ⋁_n<ρ(m) (u_n – u_<n) (since ρ is strictly monotonic, so that the sequence of indices ρ(1), …, ρ(m–1) is included in the sequence of indices 0, 1, …, ρ(m)–1),
• which is less than or equal to ⋁_n<ρ(m) u_n (because a–b≤a for all a and b in S; by definition of subtraction, that inequality is equivalent to a≤b ⋁ a, which is obvious),
• which is equal to u_<ρ(m).

We have obtained u_ρ(m)–u_<ρ(m) ≤ u_<ρ(m). By definition of subtraction, this is equivalent to u_ρ(m) ≤ u_<ρ(m) ⋁ u_<ρ(m), namely to u_ρ(m) ≤ u_<ρ(m). But look: we have just shown that (u_n)_{n ∈ N} is good! And that is impossible. This would finish the proof of the proposition, for the fact that we still have not proved the Claim.

Hence let us prove the Claim, namely that τ’ is good, where τ’ is the locus inside S consisting of all finite suprema (resp., all finite suprema of finite infima, resp., all suprema of finite infima) of elements in ∪_n≥1 Down(u_n)/u_<n.

Once again, we reason by contradiction. We assume a bad sequence (w_m)_{m ∈ N} in τ’. There is a map ρ : N → N such that, for each m ∈ N, w_m is in Down(u_ρ(m))/u_<ρ(m). We write w_m as v_m–u_<ρ(m), where v_m ∈ τ_α has depth strictly smaller than d(u_<ρ(m)).

If, for some k ∈ N, there were infinitely many values of m such that ρ(m)=k, say m₀<m₁< ··· <m_i< ···, then the following would happen. Let β ≝ d(u_k): we have β < α, hence by assumption τ_β is good. It follows that the sequence v_m0, v_m1, ··· , v_mi,··· is good. In other words, v_mi ≤ ⋁_j<i v_mj for some i ∈ N. Then, w_mi =v_mi–u_<k ≤ (⋁_j<i v_mj)– u_<k = ⋁_j<i (v_mj–u_<k) = ⋁_j<i (w_mj–u_<k) ≤ ⋁_j<i w_mj ≤ ⋁_p<mi w_p, contradicting the fact that (w_m)_{m ∈ N} is bad.

Hence, for every k ∈ N, there are only finitely many values of m such that ρ(m)=k. In particular, the sequence (ρ(m))_{m ∈ N} cannot be bounded, and therefore it has a strictly monotonic subsequence. It follows that, taking subsequences if necessary, we may assume that ρ itself is strictly monotonic. By item 1 of the massaging lemma, the corresponding subsequence of (w_m)_{m ∈ N}, which we will write as (w_m)_{m ∈ N} again, is bad, too.

This being done, we define a new sequence (u’_n)_{n ∈ N} of elements of ∪_β<α τ_β as u₀, u₁, …, u_ρ(0)–1, v₀, v₁, …, v_m, … In other words, for every n<ρ(0), we let u’_n≝u_n, and for every n≥ρ(0), we let u’_n≝v_n–ρ(0). Since u’_ρ(0)=v₀ has depth strictly smaller than d(u_<ρ(0)), which is smaller than or equal to d(u_ρ(0)) since ρ is monotonic, this new sequence is strictly smaller than (u_n)_{n ∈ N} in the lexicographic extension of the depth ordering, and is therefore good. We obtain that u’_n ≤ ⋁_m<n u’_m for some n ∈ N. But, as we now claim, this is impossible:

• If n<ρ(0), then we obtain that u_n ≤ ⋁_m<n u_m, contradicting that (u_n)_{n ∈ N} is bad.
• If n≥ρ(0), then, letting m≝n–ρ(0), we have that u_n=v_m is less than or equal to in (⋁_i<ρ(0) u_i) ⋁ v₀ ⋁ v₁ ⋁ … ⋁ v_m–1 = u_<ρ(0) ⋁ v₀ ⋁ v₁ ⋁ … ⋁ v_m–1. Hence (and using the fact that a–b is monotonic in a), w_m = v_m–u_<ρ(m) is less than or equal to the supremum of:
  • u_<ρ(0)–u_<ρ(m), which is equal to ⊥, since ρ(0)≤ρ(m) (ρ is monotonic): indeed u_<ρ(0)≤u_<ρ(m), and the properties of subtraction imply that for all a, b with a≤b, a–b is the least element ⊥ (for every w in S, a–b≤w if and only if a≤b ⋁ w, which is simply true);
  • the elements v_j–u_<ρ(m), for each j such that 0≤j<m, which are all less than or equal to v_j–u_<ρ(j) since ρ(j)<ρ(m) (ρ is monotonic) and since subtraction is antitonic in its second argument; in other words, they are all less than or equal to w_j.
  • Summing up, w_m is less than a supremum of elements which are equal to ⊥ or to w_j with 0≤j<m. Therefore w_m ≤ ⋁_i<m w_i, and that is impossible since (w_m)_{m ∈ N} is bad.

Hence, as promised, we have reached a contradiction. This finishes to prove the Claim, and that was the last thing we had to prove in order to prove the Proposition (phew!). ☐

We are almost there. We induct on the ordinal α in order to show that τ_α is well-defined and good for every α. (In that case, they form an ascending chain of loci inside S, as we have noticed earlier). Since we start from a good locus τ₀ by assumption, this is true for α=0. If that is true for α, then that is also true for α+1, since τ_α+1=E(τ_α) and E maps good loci to good loci. If α is a limit ordinal and τ_β is well-defined and good for every β<α, then τ_α is also good by the Proposition.

By cardinality matters, the ascending sequence of loci τ_α must eventually stabilize at some ordinal. (Otherwise there would be as many such distinct loci as there are ordinals, but that is impossible since ordinals form a proper class, not a set.) It is clear that the first ordinal α such that τ_α+1=τ_α cannot be a limit ordinal, too. Hence we have proved:

Theorem. Let S be a universe (namely, a sup-semilattice with subtraction, resp. a Boolean algebra, resp. a complete Boolean algebra), E be an expander on S, and τ₀ be a good locus S such that τ₀ ⊆ E(τ₀) (where a locus is a subsemilattice, resp. a sub-(bounded lattice), resp. a subframe). Then E has a least fixed point above τ₀ in the poset of good loci. Explicitly, one can define larger and larger good loci τ_α of S by induction on the ordinal α, by:

1. τ₀ is already defined;
2. τ_α+1≝E(τ_α) for every ordinal α;
3. τ_α is the locus generated by the union of the subsemilattices τ_β, β<α, when α is a limit ordinal.

The good loci τ_α form an ascending chain, and the least fixed point of E above τ₀ is obtained as τ_α, where α is the first ordinal such that τ_α+1=τ_α, necessarily a non-limit ordinal.

We obtain Aliaume’s master theorem as a corollary: we let S be the complete Boolean algebra P(X), where X is a fixed set, and we define loci as subframes, namely as topologies on X.