L-domains, stable open sets and stable Stone duality

Stone duality relates topological spaces and locales (or frames). But there are really many sorts of Stone dualities. I have already mentioned a personal one here between convergence spaces and so-called convergence coframes.

In 1997, Yixiang Chen studied Stone dualities that relate so-called L-domains to so-called distributive D-semilattices. He called the latter slightly differently in [1], and I am using the name that he and Achim Jung used in [2].

Explaining all this will give me the opportunity to explain what an L-domain is. As in [2], I will not require L-domains to be continuous or algebraic, although, as we will see, algebraicity lurks behind. To be fair, most of this blog post will be a paraphrase of selected parts of [2], and most specifically Section 5.

L-domains

An L-domain is a dcpo X in which every principal ideal ↓x is a complete lattice. That is a very subtle notion. We equip each principal ideal ↓x with the ordering inherited from X, but that does not mean that suprema are computed as in X (or even exist in X).

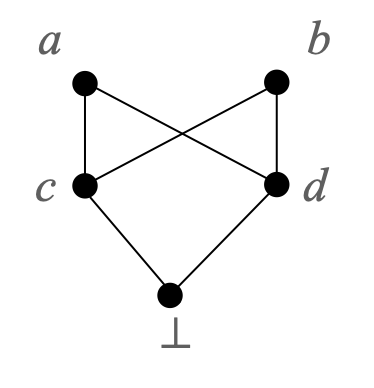
The following example should be kept in mind.

This is an L-domain, in fact even an algebraic L-domain, and one that is not a complete lattice. In order to verify that it is an L-domain, look: ↓a is the four-element complete lattice {a, c, d, ⊥}, ↓b is the four-element complete lattice {b, c, d, ⊥}, ↓b is the two-element complete lattice {c, ⊥}, similarly for ↓d, and ↓⊥={⊥} is trivially a complete lattice.

This example is important because it illustrates the following pitfall: all the principal ideals ↓x are ordered by the same ordering (rather, the restriction to ↓x of the same ordering), but suprema in those complete lattices may differ.

In the example above, notably, the supremum of {c, d} in ↓a is a, but its supremum in ↓b is b instead. Please do check this for yourself, until you understand what happens!

It is traditional to write y ⋁_x z for the supremum of two elements y and z in ↓x.

There is no similar difficulty for non-empty infima. If F is a non-empty family of elements of X, which are all both in ↓x and in ↓y, then the infimum of F in ↓x coincides with the infimum of F in ↓y, and is in fact the infimum of F in X. This is because the lower bounds of F in each of ↓x, ↓y, and X, are the same.

However, please (once again) pay attention that I said non-empty infima, namely infima of non-empty families. The infimum of the empty family in ↓x is the largest element of ↓x, namely x, and that definitely differs from the infimum of the empty family in ↓y if y≠x.

It is useful to realize that L-domains can be characterized in another way, which does not rely on this error-prone notion of lattices ↓x whose suprema may vary when we change x. A subset A of a poset X is consistent if and only if it is non-empty and has an upper bound.

Lemma ([2], Proposition 5.1). A dcpo X is an L-domain if and only if every consistent subset has an infimum.

Proof. Let X be an L-domain, and A be a consistent subset of X. By definition, A has an upper bound x, so A is included in ↓x. Since A is consistent, it is non-empty, and we have seen that its infimum in ↓x is in fact its infimum in X.

Conversely, let X be a dcpo in which every consistent subset has an infimum. Let x be an arbitrary point in X. For every family A of elements of ↓x, either A is empty and then A admits x as infimum in ↓x, or A is non-empty, and then A is consistent, hence has an infimum in X. It is easy to see that this must also be the infimum of A in ↓x, since the lower bounds of A in X and in ↓x are the same. This shows that ↓x has arbitrary infima. This implies that it also has arbitrary suprema (the supremum of A being computed as the infimum of its set of upper bounds in ↓x), so ↓x is a complete lattice. ☐

Stable maps

There is a category of L-domains and Scott-continuous maps. This is a very nice category, and, if I am correct, it is Cartesian-closed: products are the expected ones, and one can check directly that every family (f_i)_{i ∈ I} of Scott-continuous maps all below a fixed Scott-continuous map f has a supremum in ↓f, which simply maps every x to the supremum of (f_i(x))_{i ∈ I} in ↓f(x). (Infima of consistent sets seem harder to describe.)

The category of continuous L-domains and Scott-continuous maps is also Cartesian-closed. For that, we show that every Scott-continuous map f from a continuous L-domain X to a continuous L-domain Y can be approximated by a directed family of step functions below f. In fact, the category of continuous L-domains is one of the two maximal Cartesian-closed full subcategories of continuous dcpos and Scott-continuous maps [3].

We will concentrate on another category: the category of L-domains and stable continuous maps. The notion of stability originates from Gérard Berry’s work on dI-domains and stable maps, with the aim of finding semantical characterizations of sequential computation [4]. The point is that, when you give semantics to a programming language where types are interpreted as dcpos and programs as Scott-continuous maps, you will obtain maps that can only be implemented by some inherently parallel computational device, such as G. Plotkin’s parallel or: B_⊥ × B_⊥ → B_⊥. (Here B_⊥ = {true, false, ⊥}, ordered by letting true and false be incomparable, and above ⊥. The parallel or is required to map (true, y) and (x, true) to true, whatever the values of x and y are, and to map (false, false) to false. This forces (⊥,⊥), (⊥,false) and (false,⊥) to be mapped to ⊥, by monotonicity. The only way to implement parallel or is to evaluate its two arguments in parallel, returning true as soon as one evaluates to true, even if the other has not terminated, and returning false only when both arguments have evaluated to false. As usual in denotational semantics, ⊥ denotes the value of computations that do not terminate.)

I will take the following as a definition, although that usually appears as an equivalent characterization: a stable function from an L-domain X to an L-domain Y is a function f that is (1) Scott-continuous (2) and preserves all infima of consistent subsets. (The image of a consistent subset by a monotone function is consistent: given any consistent family (x_i)_{i ∈ I} in X, let x be any upper bound of that family, then f(x) is an upper bound of (f(x_i))_{i ∈ I}.) Hence the latter has an infimum in Y.)

Now you may realize that parallel or is not stable: the subset {(true,⊥), (⊥,true)} is consistent, since (true, true) is an upper bound. Its infimum is (⊥,⊥), which is mapped to ⊥ by parallel or, but ⊥ is not the infimum of the image subset {true, true}. This is a good sign that stability would be a candidate for a semantical notion of sequential (not parallel) function.

It turns out that there are still inherently parallel functions among the stable functions. The most well-known is Gustave’s function. This is the function G : B_⊥ × B_⊥ × B_⊥ → B_⊥ that maps:

• every triple of the form (true, false, x), (x, true, false) or (false, x, true) to true, whatever x;
• (true, true, true) and (false, false, false) to false,
• and all other triples to ⊥.

(Oh, don’t look for a mathematician or a computer scientist named Gustave. From what I have heard, Gustave used to be Gérard Berry’s nickname in the 1970s, while he was in the so-called “bâtiment 8” group at INRIA Rocquencourt, with Gérard Huet and Gérard Boudol. When you all have the same first name, resort to nicknames! Just be sure to keep the initial.)

It is easy to see that G is monotonic, and therefore Scott-continuous, since B_⊥ × B_⊥ × B_⊥ does not have any infinite directed subset. Checking that it preserves all infima of consistent subsets is a nightmare, unless you know the following—which happens to be the official definition of “stable”—and then a further equivalent lemma.

Lemma. A monotonic function f : X → Y between L-domains preserves infima of consistent subsets if and only if for every x ∈ X and for every y ∈ Y such that y≤f(x), there is a least element x’ in X such that x’≤x and y≤f(x’).
In particular, a Scott-continuous function f : X → Y between L-domains is stable if and only if for every x ∈ X and for every y ∈ Y such that y≤f(x), there is a least element x’ in X such that x’≤x and y≤f(x’).

Proof. In one direction, let f be stable and let us assume y≤f(x). Since X is an L-domain, the family A≝f^–1(↑y) ∩ ↓x, which is consistent (as it is included in ↓x), has an infimum x’. Since f preserves infima of consistent sets, f(x’) is the infimum of the direct image f[A] = {f(x”) | x”≤x and f(x”)≥y}, which is certainly larger than or equal to y. Also, x’≤x, so x’ is in A, showing that x’ is in fact the least element of A, namely the least element x’ of X such that x’≤x and y≤f(x).

In the other direction, let A be a consistent subset of X: hence A is included in ↓x for some x in X. Let also y be the infimum of the consistent set f[A], which exists since the latter is consistent (because f is monotonic) and since Y is an L-domain. We wish to show that y=f(inf A). We have y≤f(x), since A is non-empty and any of its points is below x. Hence, by assumption, there is a least element x’ in X such that x’≤x and y≤f(x’). All the elements x” of A are such that x”≤x (since A is included in ↓x) and y≤f(x”) (because y is the infimum of f[A]), so they are all larger than or equal to the least element x’ with those properties. This entails that x’≤inf A. Since f is monotonic, f(x’)≤f(inf A), so y≤f(inf A), since y≤f(x’). We also have f(inf A)≤y=inf f[A], by monotonicity of f. ☐

The Lemma does not say that f^–1(↑y) is empty or has a least element: for each x in f^–1(↑y), there is a least element x’ in f^–1(↑y) below x. If you take two elements x₁ and x₂ in f^–1(↑y), those least elements x’₁ and x’₂ in f^–1(↑y) respectively below x₁ and below x₂ may be different. Hence we have two cases:

• x’₁ and x’₂ are equal. This happens notably if x₁ and x₂ form a consistent set, namely if they have a common upper bound x. Indeed, in that case the least element in f^–1(↑y) below x₁ coincides with the least element in f^–1(↑y) below x₂, and with the least element in f^–1(↑y) below x.
• Or x’₁ and x’₂ are different. In that case, I claim that they must form an inconsistent set, namely that ↑x’₁ and ↑x’₂ do not intersect. Otherwise, since X is an L-domain, x’₁ and x’₂ would have an infimum x’, and since f is stable, it must preserve that infimum, so that f(x’)=inf (f(x’₁),f(x’₂))≥y. In particular, x’ is in f^–1(↑y) and below x’₁≤x; since x’₁ is the least element of f^–1(↑y) below x₁, this implies that x’₁≤x’. But remember that x’ is the infimum of x’₁ and x’₂, so x’≤x’₁, whence x’=x’₁. Similarly, x’=x’₂, and therefore x’₁=x’₂, which is impossible.

Therefore:

Proposition. A monotonic (resp., Scott-continous) function f : X → Y between L-domains preserves infima of consistent subsets (resp., is stable) if and only if for every y ∈ Y, f^–1(↑y) is a union of pairwise disjoint principal filters ↑x’.

Let us check that Gustave’s function G is stable. We look at f^–1(↑y) for all possible values of y.

• f^–1(↑true) consists of the triples (true, false, x), (x, true, false) or (false, x, true), for every x: that is the union of the principal filters ↑(true, false, ⊥), ↑(⊥, true, false), ↑(false, ⊥, true), and those are indeed pairwise disjoint;
• f^–1(↑false) consists of (true, true, true) and (false, false, false), which is the disjoint union of the principal filters ↑(true, true, true) and ↑(false, false, false);
• f^–1(↑⊥) is the whole space of all triples, which is the single principal filter ↑(⊥, ⊥, ⊥).

Hence G is indeed stable. But you cannot implement it in a purely sequential fashion, as you need to evaluate all three of its arguments in parallel. (You can make this into a formal argument, but that would take me too far, using Jung and Tiuryn’s logical relations of varying arity or Ehrhard’s hypercoherences.)

Stable maps and finite elements

If f is stable, then for element y of Y, f^–1(↑y) is a union of pairwise disjoint principal filters ↑x’, where x’ is necessarily minimal in f^–1(↑y). If additionally y is finite (namely, way-below itself), then ↑y is Scott-open, so f^–1(↑y) is Scott-open as well, since f is Scott-continuous. We claim that all the elements x’ are finite. This is because of the following.

Lemma. If a Scott-open set U can be written as a disjoint union of principal filters ↑x’, then each of the elements x’ is finite.

Proof. For every directed family (x_i)_{i ∈ I} whose supremum x is above one such element x’, x is in U, so some x_i is in U already. By assumption x_i must be in a principal filter ↑x”, for some minimal element x” of U. If x’=x”, then we are done: x’≤x_i establishes that x’ is finite. Otherwise ↑x’ and ↑x” are disjoint (by assumption), but x”≤x_i≤x, while x’≤x, and that is impossible. ☐

This entails that if Y is an algebraic L-domain, and X is a mere L-domain, then a function f : X → Y is stable if and only if for every finite element y of Y, f^–1(↑y) is a disjoint union of principal filters ↑x’ with x’ finite.

Stable open sets

Let us say that a subset U of an L-domain X is a stable open set if and only if its characteristic function χ_U is a stable function from X to Sierpiński space S = {0 < 1}. Then U = χ_U^–1(↑1) must be a disjoint union of principal filters ↑x’, where each x’ is finite in X, as we have just seen, using the fact that S is an algebraic L-domain.

Conversely, any disjoint union U of principal filters ↑x’_i, i ∈ I, where each x’_i is finite in X, is stable open. We just have to check that χ_U preserves infima of consistent subsets, or equivalently that given any consistent family F, say with upper bound x, such that F is included in U, then inf F is also in U. Since F is consistent, it is non-empty, and since U is upwards-closed, x must be in U. Then there is a unique index i ∈ I such that x is in ↑x’_i, and then x’_i≤inf F, so inf F is indeed in U.

Let me sum up:

• A stable open subset of an L-domain X is a disjoint union of principal filters ↑x’_i, i ∈ I, where each x’_i is finite in X;
• A stable open subset of an L-domain X is a Scott-open subset U such that, for every consistent family F included in U, inf F is in U.

In general, the stable open subsets of an L-domain do not generate its (Scott) topology. For example, consider the complete lattice [0, 1]. As a complete lattice, it is an L-domain. It only has one finite element, 0, so its only stable open sets are [0, 1] and the empty set, which is far from enough to generate the Scott-open subsets of [0, 1].

However, if X is an algebraic L-domain, then every Scott-open subset is a union of sets of the form ↑x’ with x’ finite, and all those sets are stable open. Hence the stable open sets form a base of the Scott topology in that case.

It is now easy to verify that:

• For every stable function f : X → Y between L-domains, the inverse image f^–1(V) of any stable open subset V of Y is stable open (indeed, χ_V o f is stable, since clearly the composition of any two stable maps is stable, and χ_V o f is simply the characteristic function of f^–1(V)).
• If f : X → Y is a function between L-domains such that the inverse image f^–1(V) of any stable open subset V of Y is stable open, and if Y is algebraic, then f is a stable map. Indeed, the stable open subsets form a base of the Scott topology on Y, so f is continuous, hence Scott-continuous. Additionally, every subset ↑y with y finite in Y is stable open, so by assumption f^–1(V) is stable open, hence a disjoint union of principal filters whose least elements are finite, so f is stable.

D-semilattices and distributive D-semilattices

The collection sn(X) of all stable open subsets of an L-domain X is such that:

• sn(X) is closed under disjoint unions (even infinite ones), namely under unions of pairwise disjoint families of stable open sets; this is easy to see if we use the definition of stable open sets as disjoint unions of principal filters ↑x’, where each x’ is finite;
• sn(X) is closed under finite intersections; this is easy to see if we use the characterization of stable open sets as Scott-open sets that are closed under infima of consistent subfamilies.

This leads to the following definition. A D-semilattice (short for disjunctive semilattice) is a poset L such that:

• Every finite subset of L has an infimum; we write ⊤ for the infimum of the empty family, and u ⋀ v for the infimum of u and v.
• L itself has a least element ⊥. This allows us to say that two elements u and v of L are disjoint if and only if u ⋀ v=⊥.
• Every disjoint subset D of L has a supremum ⩒D. (A subset is disjoint if and only if it consists of pairwise disjoint elements.) I will also write this as ⩒_{i ∈ I} u_i if D=(u_i)_{i ∈ I}, and I will call such special suprema disjoint suprema.

Additionally, a D-semilattice is distributive if and only the law u ⋀ ⩒_{i ∈ I} v_i = ⩒_{i ∈ I} (u ⋀ v_i) holds. This is the same thing as the frame distributivity law, except with disjoint suprema instead of arbitrary suprema.

This definition is tailored to sn(X): sn(X) is always a distributive D-semilattice, with finite intersections for finite infima, and disjoint unions for disjoint suprema.

Additionally, for every stable map f : X → Y between L-domains, there is a map sn(f) : sn(Y) → sn(Y), which sends every stable open subset V of Y to f^–1(V). This map preserves all finite infima and all disjoint suprema. In other words:

• There is a category LDom of L-domains and stable maps.
• There is a category dDSL of distributive D-semilattices, whose morphisms are the maps that preserve finite infima and disjoint suprema.
• sn defines a functor from LDom to the opposite category dDSL^op.

The points of a disjunctive D-semilattice

The functor sn has a right adjoint, as we will see, and the construction is very similar to ordinary Stone duality. We observe that Sierpiński space S is also a distributive D-semilattice, simply because it is a frame, and then we define a point of a distributive D-semilattice L as a morphism φ : L → S in dDSL.

In order to make a comparison, in ordinary Stone duality, we defined the points of a frame as its completely prime filters F. Those are exactly the sets whose characteristic maps χ_F are frame homomorphisms to S (exercise!). Doing the exercise in reverse in our case gives us the following: a point of a distributive D-semilattice L is the characteristic map χ_F of disjunctively completely prime filters F in L, namely subsets such that:

• ⊤ is in F;
• for all u, v in F, u ⋀ v is in F;
• for every disjoint subset D of L, if ⩒D is in F, then some element of D must be in F already.

We let pt(L) be the set of points of L. In traditional Stone duality, we would put a topology on pt(L), but one surprising aspect of the construction in [2] is that one should use the obvious ordering on pt(L) (inclusion of completely prime filters=the pointwise ordering on morphisms from L to S), and this makes pt(L) an L-domain right away.

In the sequel, we adopt the view that pt(L) consists of disjunctively completely prime filters, ordered by inclusion, since that will most probably make our arguments more readable; Chen and Jung make the same choice.

Lemma. For every distributive D-semilattice L, pt(L) is an L-domain. Directed suprema are computed as unions, intersections of consistent families are computed as intersections.

(Oh, is it an algebraic L-domain? The answer is at the end of this page.)

Proof. It is fairly easy to see that pt(L) is a dcpo, and the supremum of a directed family (F_i)_{i ∈ I} of disjunctively completely prime filters is the union F≝∪_{i ∈ I} F_i. In order to verify this, it is enough to check that F is a disjunctively completely prime filter.

• ⊤ is in F, because it is in F_i, for any i ∈ I (I is non-empty);
• for any two elements u and v of F, u is in some F_i, v is in some F_j, by directedness F_i and F_j are included in some F_k, and then u ⋀ v is in F_k, hence in F;
• for every disjoint subset D of L, if ⩒D is in F, then if ⩒D is in some F_i, so there is an element u of D in some F_i, hence in F.

In order to show that pt(L) is an L-domain, we claim that any consistent family in pt(L) has an infimum. Let therefore (F_i)_{i ∈ I} be a consistent family of disjunctively completely prime filters of L. Since it is consistent, I is non-empty, and there is a disjunctively completely prime filter F that contains every F_i. We claim that the intersection G≝∩_{i ∈ I} F_i is the desired infimum. It suffices to check that it is a disjunctively completely prime filter.

• ⊤ is in G, because it is in every F_i;
• for any two elements u and v of G, u ⋀ v is in every F_i, hence in G;
• for every disjoint subset D of L such that ⩒D is in G, we have that for every i ∈ I, ⩒D is in F_i, so there is an element u_i in D that is also in F_i. There seems to be a difficulty: there is apparently no reason why the elements u_i would be equal.
  But look more closely: the family D is disjoint, so any two distinct elements u_i and u_j among those that we have found must be such that u_i ⋀ u_j = ⊥. Then, u_i is in F_i, u_j is in F_j, hence both are in F (this is where we use the fact that the family (F_i)_{i ∈ I} is consistent), and since F is a filter, u_i ⋀ u_j is in F. This would mean that ⊥ is in F, which is impossible: ⊥ is the supremum of the empty family (which is trivially disjoint), and disjunctive complete primality would entail that this empty family should contain an element of F, which is plainly absurd.
  In other words, all the elements u_i that we have found are equal. Since I is non-empty, they are all equal to a common element u, which is then in D and in every F_i, hence in G. ☐

Stable Stone duality

We can now turn pt into a functor from dDSL^op to LDom, by declaring that for every morphism φ : L → L’, pt(φ) maps every F’ in pt(L’) to φ^–1(F’). The latter is a point of L, because its characteristic map is simply χ_F’ o φ, which is a morphism of dDSL, as the composition of two morphisms. We check that pt(φ) is a stable function: the map F’ ↦ φ^–1(F’) preserves all intersections and all unions that make sense, in particular it is monotonic and preserves directed unions and intersections of consistent families.

Theorem [2, Theorem 5.11]. There is an adjunction sn ⊣ pt between LDom and dDSL^op. The unit η : X → pt(sn(X)) maps every point x of an L-domain X to the set of its stable open neighborhoods. The counit ε : L → sn(pt(L)) (written as a morphism in dDSL, not dDSL^op), maps every u ∈ L to the set of disjunctively completely prime filters F of L such that u ∈ F.

(Note: ε(u) is written as O_x in [2], where x stands for u.)

Proof. We first check that η(x) is a disjunctively completely prime filter. The whole space X (=⊤) is in η(x), the intersection of any two stable open sets that contain x also contains x, and any pairwise disjoint union of stable open sets that contains x must be such that one of the stable open sets contains x.

Second, we check that η is a stable map. If x≤x’, then every stable open neighborhood of x is a stable open neighborhood of x’, since every open set is upwards-closed: so η is monotonic. For every directed family (x_i)_{i ∈ I} with supremum x in X, every stable open neighborhood of x is a stable open neighborhood of some x_i. This shows that η(x) ⊆ ∪_{i ∈ I} η(x_i), and the converse inclusion is by monotonicity. In order to show that η is stable, let (x_i)_{i ∈ I} be any consistent family (say, with upper bound x), let x’≝inf_{i ∈ I} x_i, and let us show that η(x‘) = inf_{i ∈ I} η(x_i). The inequality η(x‘) ≤ inf_{i ∈ I} η(x_i) follows from monotonicity. The reverse inequality takes the form ∩_{i ∈ I} η(x_i) ⊆ η(x‘), and is proved as follows. Let U be any stable open subset of X that lies in ∩_{i ∈ I} η(x_i). For every i ∈ I, U is in η(x_i), so that x_i is in U. Since U is stable, x’ is in U, so U is in η(x‘).

Third, we verify that ε(u) = {F ∈ pt(L) | u ∈ F} is a stable open subset of sn(pt(L)). Clearly, ε(u) is upwards-closed. Given any directed family (F_i)_{i ∈ I} of disjunctively completely prime filters of L, with supremum (=union) F, if F is in ε(u), namely if u is in F, then u is in some F_i, so F_i is in ε(u). Therefore ε(u) is Scott-open. Given any consistent directed family (F_i)_{i ∈ I} of disjunctively completely prime filters of L in ε(u), say with upper bound F, let G≝∩_{i ∈ I} F_i be its infimum. Since every F_i is in ε(u), u is in every F_i, hence in G, so G is in ε(u).

Fourth, we verify that ε is a morphism of distributive D-semilattices, namely that its preserves finite infima and disjoint suprema. For finite infima, we have ε(⊤)=pt(L), since every disjunctively completely prime filter contains ⊤, and ε(u ⋀ v) = ε(u) ∩ ε(v), since the elements F of pt(L) are filters (hence u ⋀ v is in F if and only if both u and v are in F). For disjoint suprema, let (u_i)_{i ∈ I} be a disjoint family in L, with (disjoint) supremum u. For every F ∈ pt(L), u is in F if and only if some u_i is in F, because F is disjunctively completely prime. Hence ε(u) is the union of the sets ε(u_i), and this is their supremum in sn(pt(L)).

Finally, we check the two adjunction laws:

• pt(ε) o η : pt(L) → pt(sn(pt(L))) → pt(L) should be the identity map. A confusing point here is that we have ε : L → sn(pt(L)), and I have written pt(ε) as the second arrow, from pt(sn(pt(L))) → pt(L), apparently in the wrong direction. You should keep in mind that ε is an arrow L → sn(pt(L)) in dDSL, hence an arrow from sn(pt(L)) to L in dDSL^op, to which we apply the function pt.
  In any case, pt(ε) o η maps every point (=disjunctively completely prime filter) F of L to pt(ε) (η (F)) = ε^–1 (η (F)) = {u ∈ L | {F‘ ∈ pt(L) | u ∈ F‘} ∈ η (F)} = {u ∈ L | F ∈ {F‘ ∈ pt(L) | u ∈ F‘}} = {u ∈ L | u ∈ F} = F.
• sn(η) o ε : sn(X) → sn(pt(sn(X))) → sn(X) (arrows written in dDSL, not dDSL^op) should also be the identity map. For every stable open subset U of X, sn(η) (ε (U)) = η^–1 (ε (U)) = {x ∈ X | U ∈ η(x)} = {x ∈ X | x ∈ U} = U. ☐

The unit of stable Stone duality, and algebraic L-domains

In usual Stone duality, building the space of points of the frame of open subsets of a space X gives you the sobrification SX of X, and the unit X → SX is injective, a topological embedding if X is T₀, and a bijection if and only if it is a homeomorphism if and only if X is sober.

Here we have the surprising fact that the unit η : X → pt(sn(X)) is always surjective.

Proposition [2, Theorem 5.14]. For every L-domain X, every disjunctively completely prime filter of stable open subsets of X is the filter of stable open neighborhoods of some point x of X. In other words, the unit η : X → pt(sn(X)) is surjective.

Proof. Let F be a disjunctively completely prime filter of stable open subsets of X. We have seen that a stable open subset U of X is a disjoint union of sets of the form ↑x’, where x’ is finite. If such a set U is in F, then one of its summands ↑x’ must be in F, since F is disjunctively completely prime. Let D be the set of finite points x’ such that ↑x’ is in F. Hence F is the collection of stable open neighborhoods of points of D.

D is non-empty, otherwise F would be empty, and that is impossible since the top element (X itself) is in F. Given any two elements x’₁ and x’₂ in D, ↑x’₁ and ↑x’₂ are in F, so their intersection is in F, too. That intersection is a stable open set in F, and we have just seen that it must therefore contain a summand ↑x’ with x’ finite. In other words, x’ is an element of D, and since x’ is in ↑x’₁ ∩ ↑x’₂, we conclude that D is directed.

Let x be the supremum of D. For every stable open set U, x is in U if and only if some element of D is in U (using the fact that U is Scott-open), if and only if U is in F (as we have seen in the first paragraph of this proof). This shows that F is exactly the collection of stable open neighborhoods of x. ☐

This begs the question: when is η an order isomorphism? Well, exactly when there are enough stable open subsets of X to separate the points of X, namely when for all points x≰x’, there is a stable open set containing x but not x’. Hence, for example, [0,1] with its only two stable open sets [0,1] and ∅, is an L-domain which will separate no point whatsoever. The implication 3 ⇒ 1 in the following proposition is Theorem 5.14 of [2].

Proposition. The following are equivalent for an L-domain X:

1. η : X → pt(sn(X)) is an order isomorphism;
2. The stable open subsets of X separate the points of X;
3. X is algebraic.

Proof. 1 ⇒ 2: if x≰x’, then by 1 η(x) must be strictly included in η(x’), so there is an element of η(x’) (a stable open neighborhood U of x’) that is not in η(x) (U does not contain x).

2 ⇒ 3. We first show that, under the assumption 2, every point x of X is the supremum of the family D of finite elements x’≤x. In order to see this, we form the supremum y of D in the complete lattice ↓x. Clearly, y≤x. If y were different from x, then we would have x≰y. Using 2, there would be a stable open neighborhood U of x that does not contain y. We write U as a disjoint union of principal filters ↑x‘_i, i ∈ I, where each x’_i is finite in X. Since x is in U, we must have x‘_i≤x for some i ∈ I. In particular, x‘_i is in D, so x‘_i≤y, since y is the supremum of D in ↓x. But that would entail that y is in U, which is impossible.

Next, we show that D is directed. We consider any finite list x‘₁, …, x‘_n of elements of D. Since x‘₁, …, x‘_n are finite, ↑x‘₁, …, ↑x‘_n are stable open sets. They all contain x, so their intersection U ≝ ↑x‘₁ ∩ … ∩ ↑x‘_n is a stable open neighborhood of x. We can write U as a disjoint union of principal filters ↑x‘ with x’ finite, so one of them contains x. It follows that x’ is in D, and since x’ is in U = ↑x‘₁ ∩ … ∩ ↑x‘_n, x’ is above x‘₁, …, x‘_n.

We conclude that x is the supremum of a directed family of finite elements below x. Since x is arbitrary, X is algebraic.

3 ⇒ 1. Since η is surjective, it suffices to show that η reflects the ordering, namely that η(x) ⊆ η(y) implies x≤y. For every finite element x’≤x, ↑x‘ is a stable open neighborhood of x, hence is in η(x), and therefore also in η(y); namely, ↑x‘ is a stable open neighborhood of y, so that x’≤y. Since x is the supremum of all such elements x’, we obtain x≤y, as desired. ☐

The algebraicization of L-domains

By analogy with ordinary Stone duality, we might imagine that pt(sn(X)) would then be an algebraic L-domain, for every L-domain X, and then a universal one that one would obtain as a kind of quotient of X (precisely, as the image by a surjective map). And that is indeed true:

Proposition. For every L-domain, pt(sn(X)) is an algebraic L-domain.

Proof. Let F be any element of pt(sn(X)), namely any disjunctively completely prime filter of stable open subsets of X. Since η is surjective, F is the collection of stable open neighborhoods of some point x in X. For every finite point x’≤x, η(x’) is included in η(x)=F. Conversely, every element U of F is a stable open neighborhood of x, and is therefore a disjoint union of sets ↑x‘ with x’ finite. One of them is below x; then U is a stable open neighborhood of x’, so U is in η(x’). It follows that F is the union of the elements η(x’), where x’ ranges over the finite elements below x.

That union is directed. It suffices to show that if x‘₁ and x‘₂ are two finite elements below x, then there is another finite element x’ below x and above x‘₁ and x‘₂. This is obvious, since ↑x‘₁ ∩ ↑x‘₂ is a stable open neighborhood of x’, and since every stable open set is a disjoint union of sets ↑x‘ with x’ finite.

Hence F is the directed union, hence also the directed supremum in pt(sn(X)), of the disjunctively completely prime filters η(x’), where x’ ranges over the finite elements below x.

It remains to show that η(x’) is a finite element of pt(sn(X)) for every finite element x’ of X. Let (F_i)_{i ∈ I} be any directed family of disjunctively completely prime filters of stable open subsets of X whose supremum (=union) contains η(x’). The stable open set ↑x‘ belongs to η(x’), so it must be an element of some F_i. Since F_i is upwards-closed, the whole of η(x’), which happens to be the collection of stable open sets that are supersets of ↑x‘, is included in F_i, and we are done. ☐

We now have a monad Alg ≝ pt o sn, with unit η, on LDom. For every L-domain X, Alg(X) is an algebraic L-domain, so let us call Alg(X) the algebraicization of X. The unit η at X is a surjective, stable map from X to Alg(X), which exhibits Alg(X) as a form of algebraic quotient of X.

Since Alg(X) is an algebraic L-domain, the unit at Alg(X) defines an isomorphism between the latter and Alg(Alg(X)). Since it is a left inverse to the monad multiplication (as with every monad), the monad multiplication is itself an isomorphism. This is the definition of an idempotent monad. All this sounds a lot like what happens with ordinary Stone duality, in which sobrification defines an idempotent monad as well.

It turns out that an adjunction whose associated monad is idempotent is called an idempotent adjunction. That notably implies that the unit η of the adjunction, evaluated at any L-domain of the form pt(L), for any distributive D-semilattice L, is an isomorphism. In turn, we have seen that this means that pt(L) is an algebraic L-domain for every distributive D-semilattice L. (I hope I haven’t made any mistake here. This sounds too good to be true!)

Conclusion

Chen and Jung also characterize the analogues of spatial frames in this context, namely the distributive D-semilattices that are of the form sn(X) for some L-domain X, up to isomorphism. Those are exactly the coprime-generated distributive D-semilattices, namely those in which every element is a disjoint supremum of coprimes; and a coprime is an element u such that for every disjoint family A whose supremum lies above u, some element of A is above u already [2, Theorem 5.17].

They also characterize L-domains through theories in a logic, much in the spirit of Scott’s information systems, but I will not explain that part now! You should not be surprised that this is a logic of entailments between formula built from finite conjunctions and disjoint disjunctions.

1. Yixiang Chen. Stone duality and representation of stable domain. Computers & Mathematics with Applications 34(1):27–41, 1997.
2. Yi-Xiang Chen and Achim Jung. A logical approach to stable domains. Theoretical Computer Science 368(1–2):124 – 148, 2006.
3. Achim Jung. The Classification of Continuous Domains. Pages 35–40 of Proceedings of the Fifth Annual IEEE Symposium on Logic in Computer Science. IEEE Computer Society Press, 1990.
4. Gérard Berry. Stable models of typed lambda-calculi. In Giorgio Ausiello and Corrado Böhm, editors, ICALP, volume 62 of Lecture Notes in Computer Science, pages 72–89. Springer, 1978.

— Jean Goubault-Larrecq (February 21st, 2022)