Plotkin’s powerdomain and the hedgehog

I would like to present a funny dcpo, which appears in an exercise in [1], and serves as a counterexample in the theory of the so-called Plotkin powerdomain. Its shape evokes a hedgehog to me, whence the title. I would first have to explain a few things about the Plotkin powerdomains. I will be very quick on that topic, because doing it in detail would take me a lot of time, and I would like to devote more time to the hedgehog itself.

Powerdomains in brief: Hoare, Smyth, Plotkin

In denotational semantics, one usually identifies three kinds of non-deterministic behavior: angelic, demonic, and erratic. This is modeled using so-called powerdomains, namely dcpos consisting of certain families of subsets. See Section 6.2 of [1] for information on all that.

For instance, angelic non-determinism is modeled using the Hoare powerdomain H(X), where X is the dcpo of possible computation states. (This was invented by Plotkin, by the way; but there will also be a Plotkin powerdomain below. Gordon Plotkin seems to prefer to call H(X) the lower powerdomain, to call the Smyth powerdomain the upper powerdomain, and to call the Plotkin powerdomain the convex powerdomain.)

H(X) can be defined as the dcpo of all non-empty closed subsets of X, with the inclusion ordering. As such, it also has the structure of an inflationary dcpo semilattice, namely it has an associative, commutative and idempotent operation + that is also Scott-continuous, and which satisfies the law a ≤ a+b. Explicitly, + is simply binary union. Categorically, H(X) is also the free inflationary dcpo semilattice over X.

Demonic non-determinism is modeled using the Smyth powerdomain. Here the topological and categorical views start to disagree. Categorically, we would like to define the Smyth powerdomain as the free deflationary dcpo semilattice over X. Topologically, we would like to define it as Q(X), the poset of non-empty compact saturated subsets of X under reverse inclusion. The two views must disagree, since Q(X) fails to be a dcpo in general. But it is a dcpo, with directed suprema computed as intersections, if X is well-filtered, and that happens notably when X is a continuous dcpo. In fact, if X is a continuous dcpo, then X is not just well-filtered, but also locally compact, and then Q(X) is a continuous dcpo again (Proposition 8.3.25 in the book). Then the topological and categorical views agree (Theorem 6.2.14 in [1]).

Erratic non-determinism, finally, is modeled using something called the Plotkin powerdomain. That one is rather elusive. Instead of two views that disagree, there are even disagreeing topological views. Here are some of the choices that we have.

1. The categorical definition, as the free dcpo semilattice over X (no inflation or deflation involved), as in [1].
2. The rounded ideal completion of the abstract basis of finitary lenses 〈E〉 under ≪_EM. A finitary lens is a set 〈E〉 ≝ ↑E ∩ ↓E, where E is a non-empty finite subset of X. The relation ≪_EM is only defined when X is a continuous dcpo (or, more generally, an abstract basis), by: 〈E〉 ≪_EM 〈F〉 if and only if every element of E is way-below some element of F and conversely, for every element of F, there is an element of E way-below it. When X is a continuous dcpo, this is isomorphic to the categorical definition (again, see [1]). One can also replace the finitary lenses 〈E〉 by those such that E is a subset of any basis of X given in advance.
3. The poset of all lenses L, under the so-called Egli-Milner ordering ≤_EM. A lens L is the intersection Q ∩ F of a compact saturated subset Q of X and of a closed subset F of X, provided that intersection is non-empty. Note that finitary lenses are special cases. Some authors instead call lens any patch-compact, order-convex subset of X, but that only coincides with this definition when X is stably compact, as far as I know. (Every lens L is patch-compact. It is also order-convex, meaning that if x≤y≤z and both x and z are in L, then y is also in L.) The Egli-Milner ordering is defined by L ≤_EM L’ if only if every element of L is below some element of L’, and every element of L’ is above some element of L (equivalently, if ↓L ⊆↓ L’ and ↑L ⊇↑ L’).
4. The poset of all lenses, under the topological Egli-Milner ordering ≤_TEM, defined by: L ≤_EM L’ if only if cl(L)⊆cl(L’) and ↑L ⊇↑ L’. This coincides with the previous relation ≤_EM when X is stably compact, because then the downward closure of a lens L (and more generally, of any patch-compact subset) is also closed, so that ↓L=cl(L). This is Exercise 9.1.43 in the book.
5. The space of A-valuations, due to Heckmann [2]. I have a soft spot for those, but I will not give their definition, and I will not consider them here.

So we have quite a choice of definitions, for not quite the same spaces. They all coincide in the case of stably compact, continuous dcpos, or even just coherent, continuous dcpos (not that there would be much of a difference, though). Definitions 1, 2, 3, and 4 are equivalent when X is a coherent continuous dcpo by Theorem 6.2.22 of [1], and definitions 2 and 5 coincide when X is a continuous dcpo by Corollary 6.2 of [2].

It turns out that Definitions 1, 2, 4 (and 5, using the same corollary) are also equivalent when X is an ω-continuous, not necessarily coherent, dcpo (Theorem 6.2.19 of [1]); in other words, when X is not just continuous, but also countably-based (see Norberg’s Lemma 7.7.13 in the book).

That is an intriguing situation. Coherence or having a countable base for the topology is enough for most, if not all, of the definitions above to produce isomorphic dcpos. Is there an example that would show that those assumptions are needed?

You have guessed it: there is one, and it is given in Exercise 6.2.23-11 of [1]. My purpose here is to describe this counter-example. Its shape is similar to a hedgehog, in that it has spines. I was tempted to call it a porcupine, too, but a porcupine has very long quills, and the spines are rather short here. The body of the hedgehog will contain uncountable directed families, but the spines will only contain countable, hence relatively short, directed families.

I will change the presentation of the hedgehog completely, by the way. In [1], it is described in an way that should make it clear how the counter-example is built so as to explicitly be a counterexample. But there are clever aspects to the construction that make it a bit miraculous somehow. I usually prefer to find a synthetic description of such counter-examples, and this is what I will do. As a result, it looks like it comes out of a hat, but verifying its properties should be somewhat simpler.

The hedgehog, part 1: the basis K

We first fix an uncountable set. Let us call it R, as we can as well imagine that it is the set of real numbers. Most of what we will do only requires it to be infinite, not uncountable, though… except showing that the hedgehog is not countably-based, and the final touch about Plotkin powerdomains.

We build the hedgehog as the ideal completion I(K) of a poset K, so that it will automatically be algebraic. Don’t worry, we will give an explicit description of I(K) later. The poset K consists of two parts:

• First, there are all the finite subsets of R, ordered by inclusion; in Exercise 6.2.23-11 of [1], those are called the white elements.
• Second, there are all the finite sequences of distinct elements of R. For example, 1;π;e_² is such a sequence, but 1;1 is not, because the elements are not distinct. In Exercise 6.2.23-11 of [1], those are called the black elements. We agree that sets and sequences are distinct. We order sequences by prefix: e.g., the sequences below 1;π;e_² are 1;π;e_² itself, 1;π, the one-element sequence 1 (again written as 1), and the empty sequence ε. I will write ‘elems σ’ for the set of elements of the sequence σ.
• Additionally, we declare that a finite set E is less than or equal a finite sequence σ if and only if E is a proper subset of elems σ.

There is no other relation between elements. In particular, no finite sequence is below any finite set. Therefore, the elements below a finite set are themselves finite sets, and the elements of K above finite sequences are themselves finite sequences. In other words, the layer of finite sets is entirely below the layer of finite sequences.

Here is how K looks like. This is only an excerpt, of course. The upper layer of sequences is shown on the right, while the lower layer of sets is shown on the left. (More comments below the picture.)

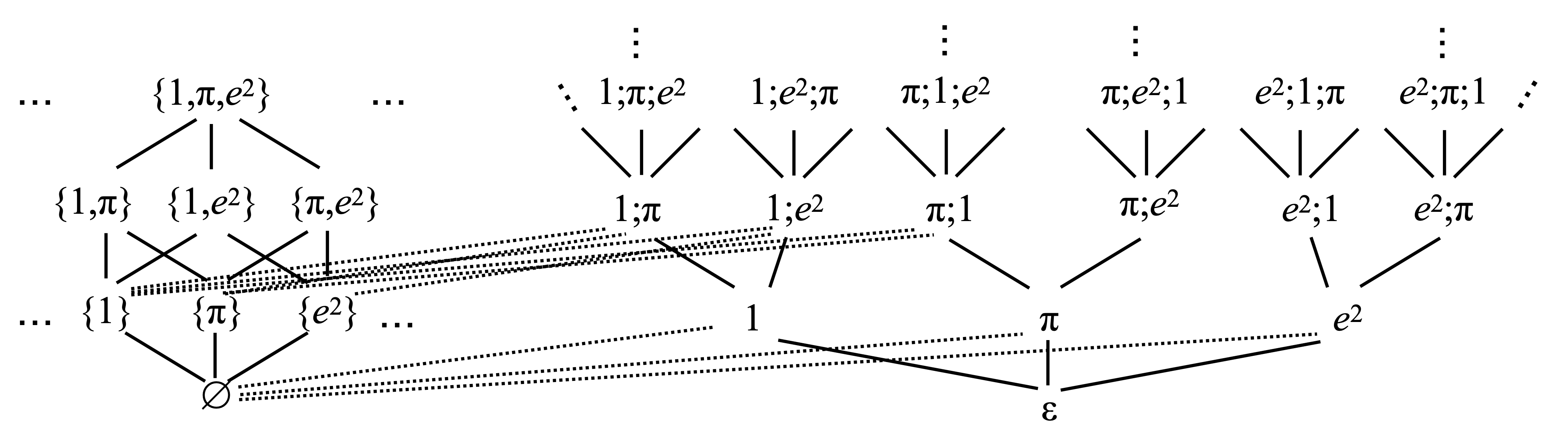
On the left, I have drawn a wee bit of the family of finite subsets of R, and the solid edges represent the basic inclusion relations. The right part displays some of the finite sequences (with pairwise distinct elements), ordered by prefix. I should have drawn a gazillion dotted edges representing the ordering relationships between sets and sequences, but that would have been really messy. Still, let us take an example. Take any sequence, for example 1;π. It has only one sequence immediately below it, and that is 1. It has two sets immediately below it, {1} and {π}. As for the elements immediately below 1;π;e_², you should find just one sequence, 1;π, and three sets: {1,π}, {1,e_²}, and {π;e_²}.

The hedgehog, part 2: the ideal completion I(K)

What do the elements of I(K) look like? We of course have all the trivial ideals obtained as downward closures of elements of K. Let us have a look at the other ideals. Let I be any non-trivial ideal in K, namely that does not contain its own supremum.

• If I only contains finite sets, then it is just an ideal of finite subsets of R under inclusion. We let A be the union of the sets in I, and then I must be equal to the set P_fin(A) of finite subsets of A.
• If I contains at least one finite sequence, we contend that there must be a unique infinite sequence ς of pairwise distinct real numbers such that I consists exactly of the finite prefixes of ς, plus all elements below them (namely, all finite subsets of elems ς; by the way, ς is the other form of the letter σ [sigma] in Greek, which you would use at the end of words).
  We prove this as follows. I contains a finite sequence σ₀. Since I is non-trivial, σ₀ is not the largest element of I, so there is an element σ’₀ in I that is not below σ₀. Since I is directed, σ₀ and σ’₀ have a common upper bound in I; let us call it σ₁. By construction, σ₀ is a proper prefix of σ₁. We repeat that process: since σ₁ is not maximal, it is a proper prefix of another element σ₂ of I, and so on. We let ς be the infinite sequence obtained in the limit; formally, its ith element is defined as the ith element of any sufficiently long finite sequence σ_n.
  Note that ς is an infinite sequence of pairwise distinct elements, too.
  Since I is downwards closed, I must contain all the finite prefixes of ς. It must also contain all the finite sets E that are properly included in elems σ_n for some n, and those are exactly the finite subsets of elems ς. (Properness does not play a rôle here. If E is a non-proper subset of elems σ_n, namely if E=elems σ_n, then E is a proper subset of elems σ_n+1, because all the elements of σ_n+1 are pairwise distinct.)
  I have not shown that ς is unique yet. But, if ς and ς’ were two distinct infinite sequences of pairwise distinct elements whose finite prefixes are all in I, we would reach a contradiction as follows: since ς and ς’ are distinct, their longest common prefix σ is finite, and then ς would be of the form σ;x;… and ς’ would be of the form σ;x’;… with x≠x’; but then the finite prefixes σ;x and σ;x‘ are both in I and simply have no common upper bound in K, which is impossible since I is directed.

Hence, I(K) is isomorphic to the following poset H. This is the hedgehog. There are two kinds of elements in H:

• The subsets of R (not necessarily finite), ordered by inclusion. This is the body of the hedgehog.
• The finite or infinite sequences of pairwise distinct elements of R, ordered by prefix. Those are the spines.
• Additionally, no sequence is below any set, and a set E is below a finite or infinite sequence ς if and only if E is a finite subset of elems ς.

Here is H, in picture. Yes, I know, I am probably overrating my animal drawing talents.

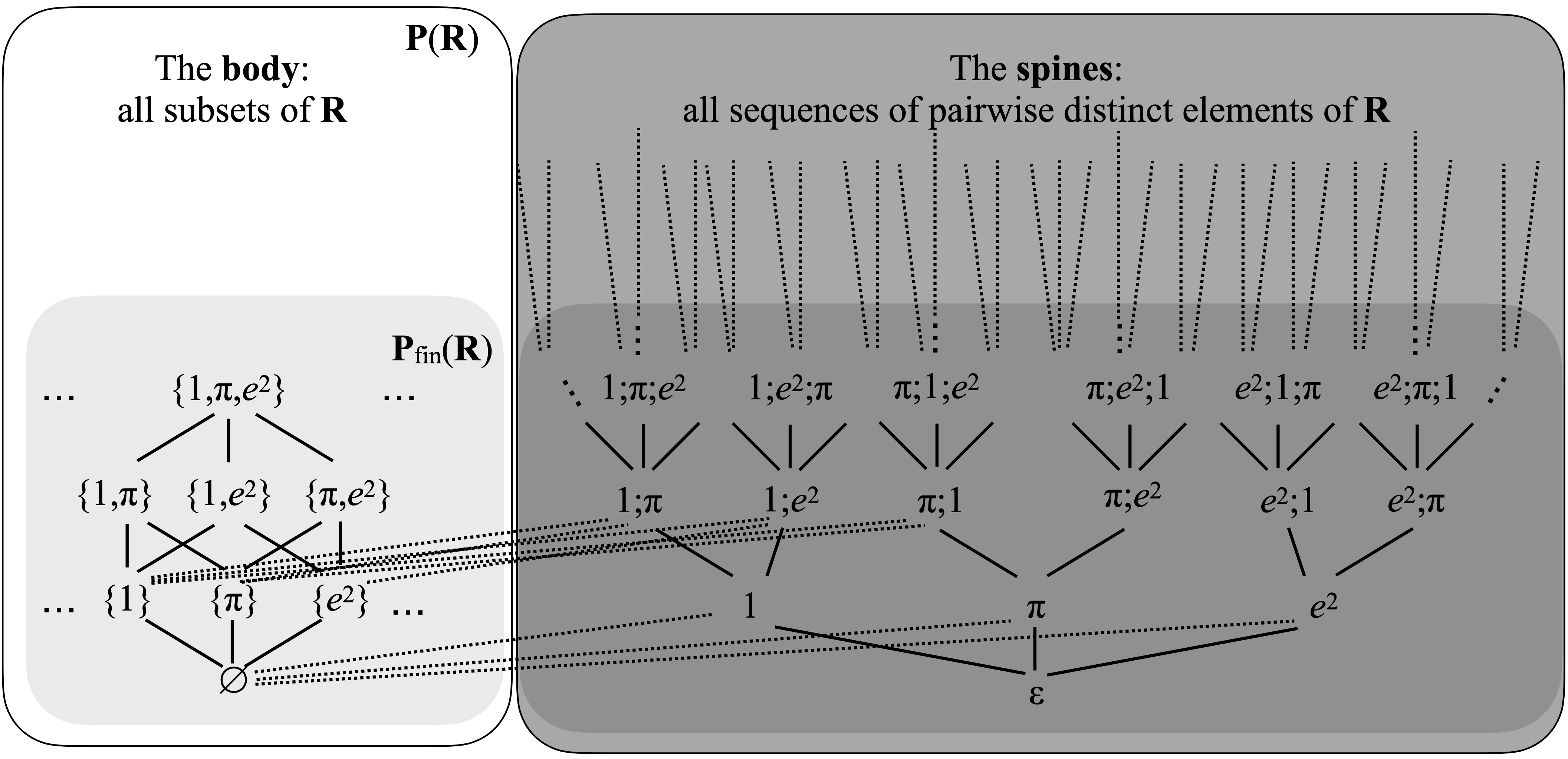
Since H is isomorphic to I(K), H is an algebraic domain, whose finite elements are the elements of K, namely the finite sets and the finite sequences, where the last two occurrences of ‘finite’ are taken in the ordinary sense of the word.

The picture may give you the impression that the spine part is much larger than the body part. However, this is exactly the opposite. The spine part has the cardinality of the continuum, namely c=2^ℵ0, the same as the cardinality of R, and is therefore much smaller than the body part, which has cardinality 2^c.

Before we go on, H is much more than an algebraic dcpo: it is even a quasi-ideal domain. Namely, all the elements below a finite element are themselves finite.

The hedgehog is not coherent, and not countably-based

Let Q₁ be the upward closure of the empty sequence ε in H. Being the upward closure of a point, it is a compact saturated set. It can be described explicitly, too: this is just the set of all finite or infinite sequences of pairwise distinct elements of R. The picture should make that clear.

Let Q₂ be the upward closure of the empty set ∅ in H. This is also a compact saturated set. As the picture shows, this is not the whole of H: it misses just one point, namely ε. Formally, a set E is below a sequence if and only if it is a proper subset of the elements of the sequence. It follows that Q₂ is the set of all subsets of R, plus the set of all non-empty finite or infinite sequences of elements of R.

We now look at Q₁ ∩ Q₂. This is the set of non-empty finite or infinite sequences of pairwise distinct elements of R. That has an open cover that consists of the upward closures ↑x of elements x of R (or rather, where x is any one-element sequence of real numbers). This open cover is minimal: if you remove just one open set ↑x from it, the result is no longer a cover—because it would miss the one-element sequence x. Quite an extreme example of an open cover without a finite subcover! It does not even have a countable subcover.

In particular, Q₁ ∩ Q₂ is not compact (it is not even Lindelöf). Therefore H is not coherent.

As for being countably-based, we know that a continuous poset is countably-based in its Scott topology if and only if it is ω-continuous, by Norberg’s Lemma (7.7.13 in the book), that is, if and only if it has a countable basis. We also know that, in an algebraic poset, there is a smallest basis, and that it consists of the finite elements (Exercise 5.1.25). Hence an algebraic poset is countably-based if and only if it has countably many finite elements. This is certainly not the case of H: there are uncountably many elements in its smallest basis K. Even just the one-element sequences, or the one-element subsets already form uncountable collections.

Therefore H is not countably-based.

Lenses of the hedgehog

We now build specific finitary lenses, as in the already mentioned exercise of [1]. For every finite subset α of R, let M_α be the subset of K consisting of:

• the element α itself (a finite set—a white element in the parlance of [1], if I may recall);
• all the finite sequences σ such that elems σ=α (those are the black elements of M_α).

M_α is finite, but pretty big: it contains |α|!+1 distinct elements, of which only one is white.

Then 〈M_α〉 is a finitary lens, by definition, but we should observe that this is just M_α. This can be shown as follows. First, we extend the notation elems k to any element k of K: we have already defined it for a sequence, and we let elems E≝E for every subset E of R. The map elems : I(K) → P(R) is monotonic, and in fact Scott-continuous. The set M_α is then just the inverse image of {α} by elems. Since {α} is (trivially) order-convex and elems is monotonic, its inverse image is also order-convex; and that immediately implies that 〈M_α〉 = M_α.

Let us look at a picture (below). When α is the set {1,π}, pictured against a blue background on the left, M_α is the collection of the three points shown against a blue background, namely {1,π}, 1;π, and π;1.

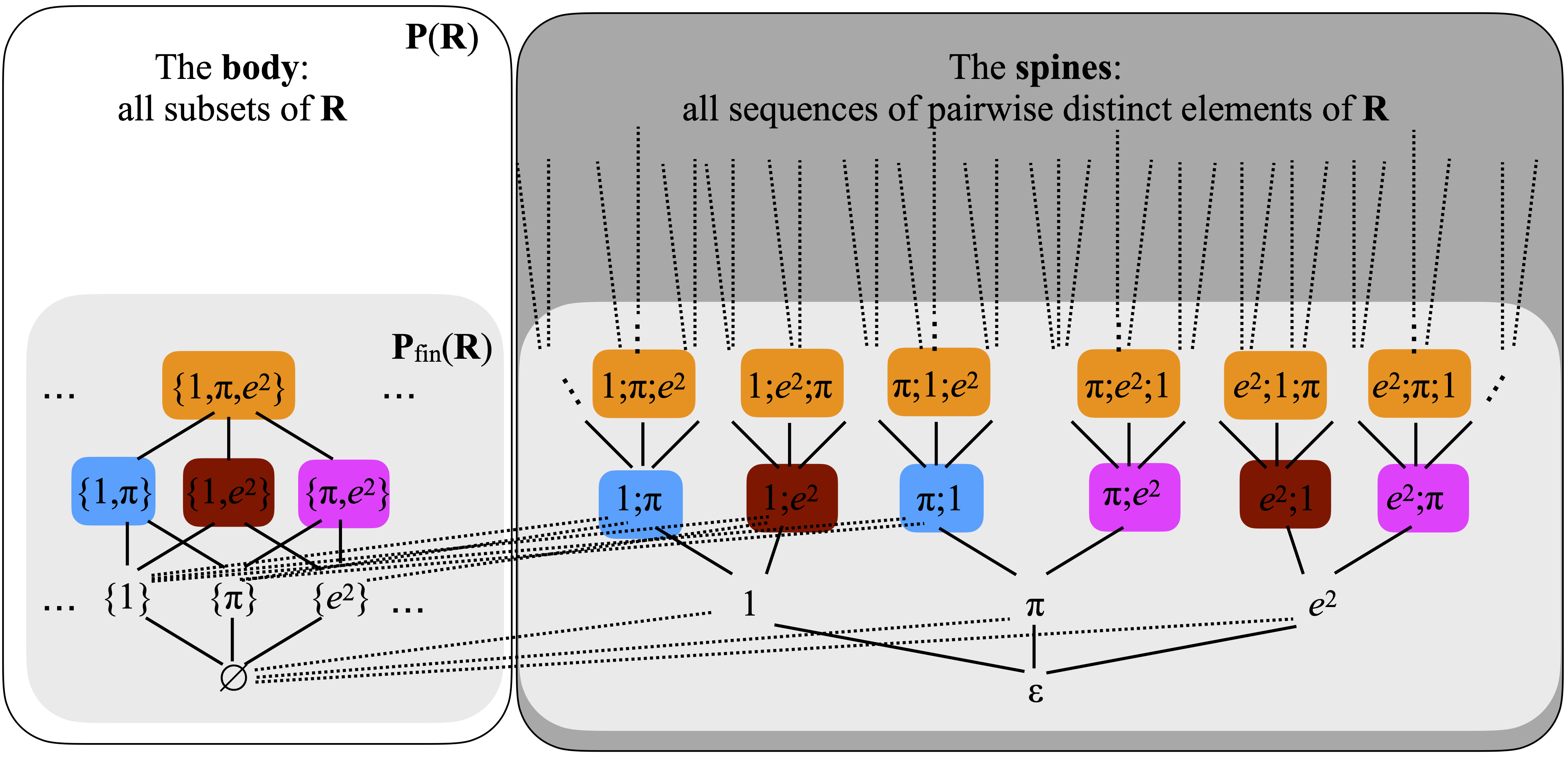
It may help to reorganize that picture, and group elements by color. This way, the sets M_α appear more clearly. Let me do that, concentrating on the elements built out of 1, π, and e^₂ alone. By now, the picture starts to match the definition of Exercise 6.2.23-11 of [1] more visibly. (Again, the dotted lines are not all the inclusion relations that exists between sets, in the body part, and sequences, in the spines part. But I have shown all of those that exist among the top four lenses—the ones I colored.)

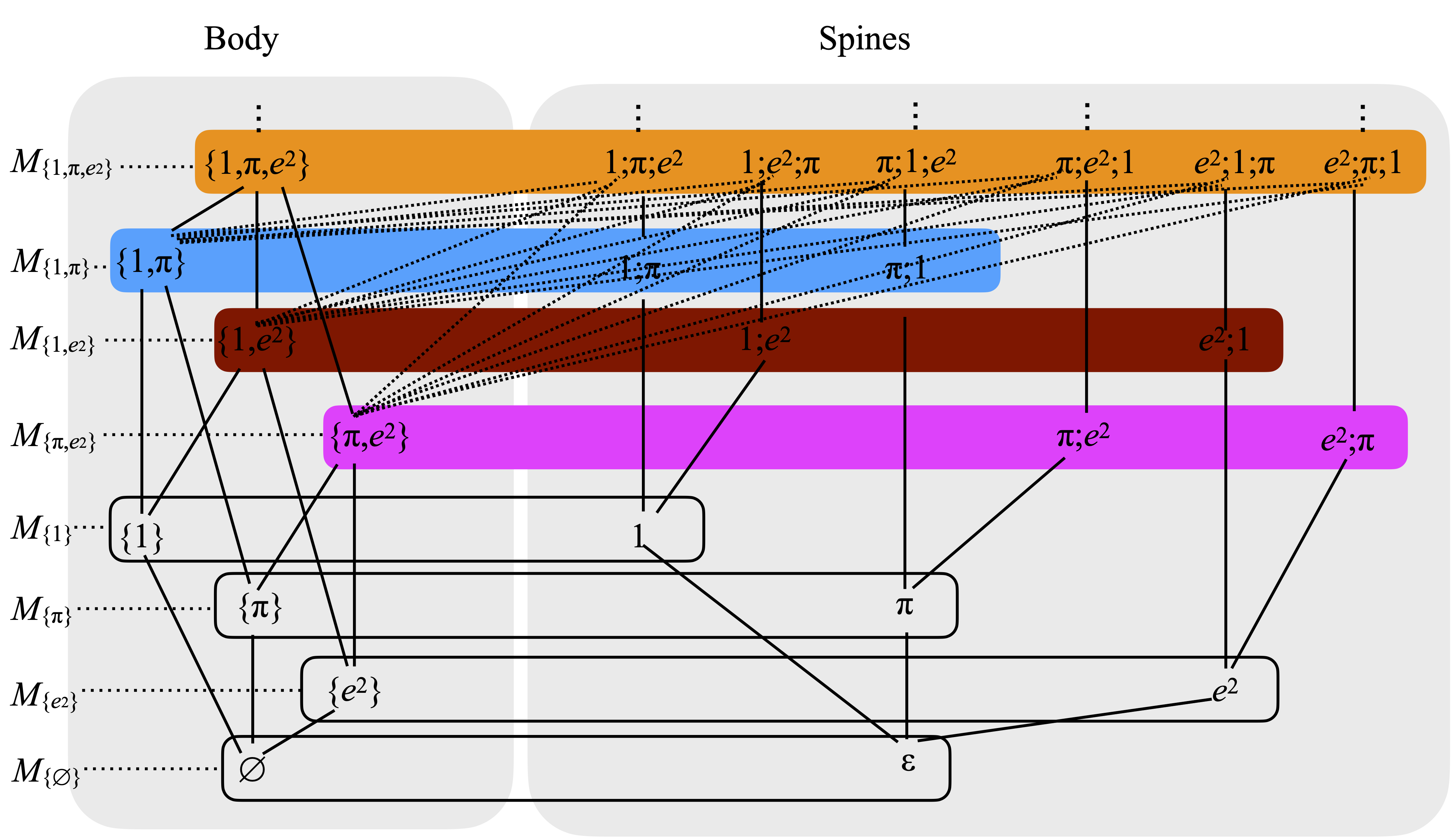
We now show that the family of all the finitary lenses M_α, when α ranges over P_fin(R), is directed.

It is of course non-empty. Next, we consider two of those lenses, M_α and M_β, and we will show that they are below some lens of the form M_γ. We simply take γ ≝ α ∪ β, because the map α ↦ M_α is monotonic, as we now claim.

Fact. For all α, β in P_fin(R), if α ⊆ β, then M_α ≤_TEM M_β, and M_α ≤_EM M_β.

Proof. Since α and β are finite, we can proceed by induction on the number of elements of β–α. Hence the proof reduces to the case where β has exactly one more element than α. Let us call that element x₀. Also, since the downward closure of a finite set is also its closure, the two statements M_α ≤_TEM M_β and M_α ≤_EM M_β are equivalent. So it is enough to show that M_α ≤_EM M_β.

We observe that the unique set (white element) α of M_α is below the white element β = α ∪ {x₀} of M_β. It is also below every sequence (black element) σ of M_β, because α is indeed properly included in elems σ = β = α ∪ {x₀}. It follows that every element of M_β is above some element of M_α—namely, its white element α. We must now show that every element of M_α is below some element of M_β. We have already seen that the white element α of M_α is below β. The other elements are sequences, namely black elements σ (with elems σ = α), and each one of them is below exactly one element of M_β, which is the extended sequence σ;x₀. Note that this is indeed a sequence whose elements are pairwise distinct, because x₀ is not in α. ☐

Comparing the Plotkin powerdomains of the hedgehog

We had five possible contenders for so-called Plotkin powerdomains. Contenders 1, 2, and 5 were isomorphic if X was a continuous dcpo. Certainly, I(K) is continuous. In fact, since it is algebraic, contender 2 has the following simpler description: it is the ideal completion I(FinLens(K)) of the family of finitary lenses over K, ordered by ≤_EM. Let me call it P₂ (“2” as in “contender 2”), but do not worry, we will not have to understand anything precise about its definition, just that it is an (algebraic) dcpo.

Let us imagine that there is an order-isomorphism φ from P₂=I(FinLens(K)) to contender 3, the poset P₃ of lenses of I(K) ordered by ≤_EM. (Reasoning with contender 4 P₄, namely with ≤_TEM, would be entirely similar.)

Well, that cannot be, because P₃ is not even a dcpo! (Remember that P₂ is.)

In order to see this, we examine the upper bounds of the directed family of lenses M_α in P₃. We will see that there is none, so that this family in particular has no supremum. We reason as follows. Let L be any lens above every M_α with respect to ≤_EM.

• We first show that L cannot contain any sequence (finite or infinite) ς. Let us imagine that it did: for every finite subset α of R, ς would be above some element k_α of M_α; but, since elems is monotonic, elems ς would have to contain elems k_α = α; since that holds for every finite subset α of R, elems ς would have to be the whole of R. But that is impossible, since elems ς, being the set of elements of a sequence, is at most countable. (This is only the second time we ever use that R is uncountable, not just infinite. The first time was to show that H is not countably-based.)
• Hence the elements of L must be subsets E of R. Each of them must be above the unique white element of each M_α, namely α, so E must be the whole of R. In other words, L must be the lens {R}.
• However, no M_α is below {R} in the ≤_EM ordering. Sure, R is above some element of M_α, namely the white element α. But none of the other elements of M_α is below any element of {R}, because no sequence is below any set in the ordering of I(K).

The same argument applies to P₄ as well: it is not a dcpo, hence is not isomorphic to P₂ either.

A final note

As I wrote that, I suddenly realized that the argument for the non-existence of upper bounds of the lenses M_α is similar to the argument used in order to show that Waterhouse’s example (see Example 2 there) of an empty projective limit is indeed empty. Note that the sequences in M_α can be encoded as injective maps from α to N. For example, 1;π;e^₂ can be encoded as the map sending 1 to 1, π to 2, and e^₂ to 3. We only obtain the injective maps from α to N whose images are initial segments of N this way, while the space at index α in Waterhouse’s example is the set of all injective maps from α to N. In spite of this, there seems to be some kind of connection between the two constructions. Most certainly a form of the Grothendieck construction. Who knows whether that construction would be fruitful in domain theory as well?

1. Samson Abramsky and Achim Jung. Domain Theory. Pages 1–168 of Abramsky, S., Gabbay, D. M., and Maibaum, T. S. E. (eds.), Handbook of Logic in Computer Science, vol. 3. Oxford University Press, 1994.  Corrected and expanded version.
2. Reinhold Heckmann. Abstract Valuations: A Novel Representation of Plotkin Power Domain and Vietoris Hyperspace. Proceedings of the 13th International Symposium on Mathematical Foundations of Programming Semantics (MFPS’97). Stephen Brookes and Michael Mislove, editors. Electronic Notes in Theoretical Computer Science 6, 1997.

— Jean Goubault-Larrecq (March 21st, 2021)