Peter Johnstone once showed the existence of a dcpo J that is not sober in its Scott topology [1]. That dcpo is not well-filtered either (Exercise 8.3.9 in the book). Is there a dcpo that is not sober but is well-filtered?
That turns out to be true, and the first one who proved this is Hui Kou [2]. There are several other constructions available to show this, and most notably a pretty simple one due to X. Xi and D. Zhao [4, Example 2]. The latter is uncountable. (Added April, 16th, 2020: and there is yet another one, due to D. Zhao, X. Xi, and Xiyang Chen [5]!) I would like to explain another simple example, due to Xiaodong Jia [3, Section 2.6], and which is countable, in addition. This is obtained, roughly, as countably many copies of J strung together.
I initially wanted to explain Xi and Zhao’s example of [5] as well, however it eventually turned out that this post was going to be long enough while just explaining how Jia’s example works. Hence I will only explain the latter. This is all the more useful as, as far as I can tell, this can only be obtained from X. Jia’s PhD thesis, which might be difficult to some.
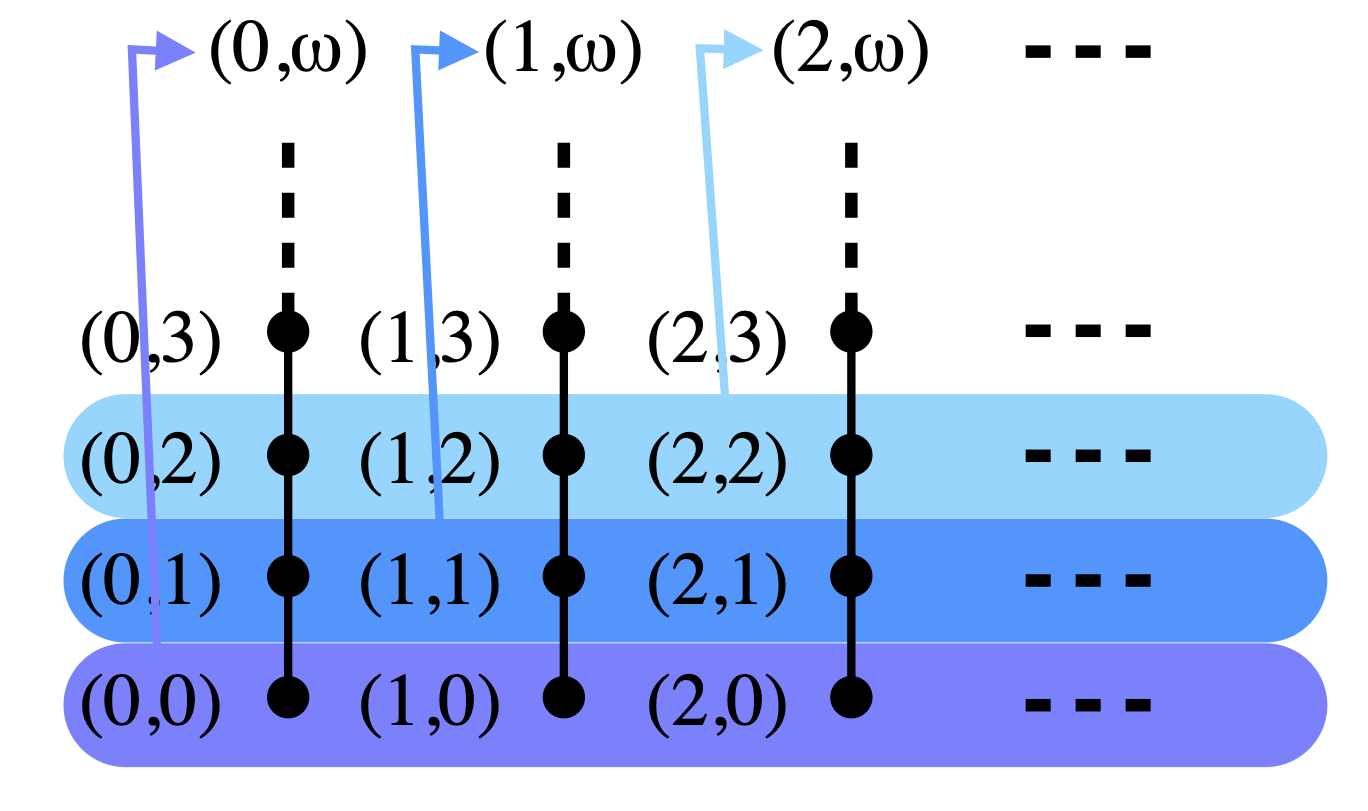
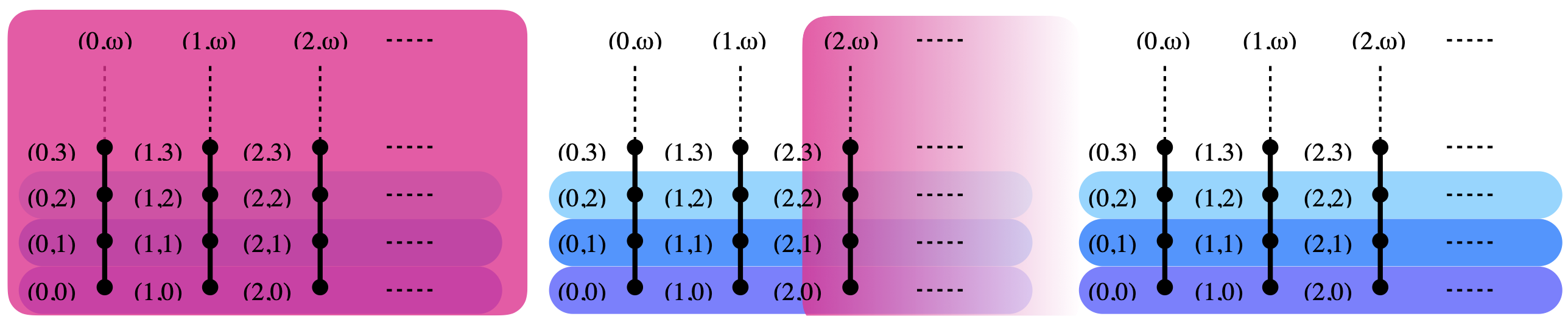
Let me recall how J is defined. This is the set of pairs (j, k) in N × (N ∪ {ω}), ordered by (j, k) ≤ (j’, k’) if and only if either j=j’ and k≤k’, or k≤j’ and k’=ω. In pictures, this is the set of points displayed below. To go up in the Johnstone ordering, you can either go up vertically, following one of the black lines; or you can follow one of the colored arrows right to the top (for example, if you are on the third row from the bottom, colored with the lightest shade of blue, you can move right to the point (2,ω ).)
X. Jia’s dcpo L is very similar. We build countably many copies of N × (N ∪ {ω}) side by side, which I will call the blocks.
We again have two ways of moving up. Either we move vertically, following one of the black lines; or we move right to the top, as in Johnstone’s dcpo J, but we also go sideways, to the block immediately to the right:
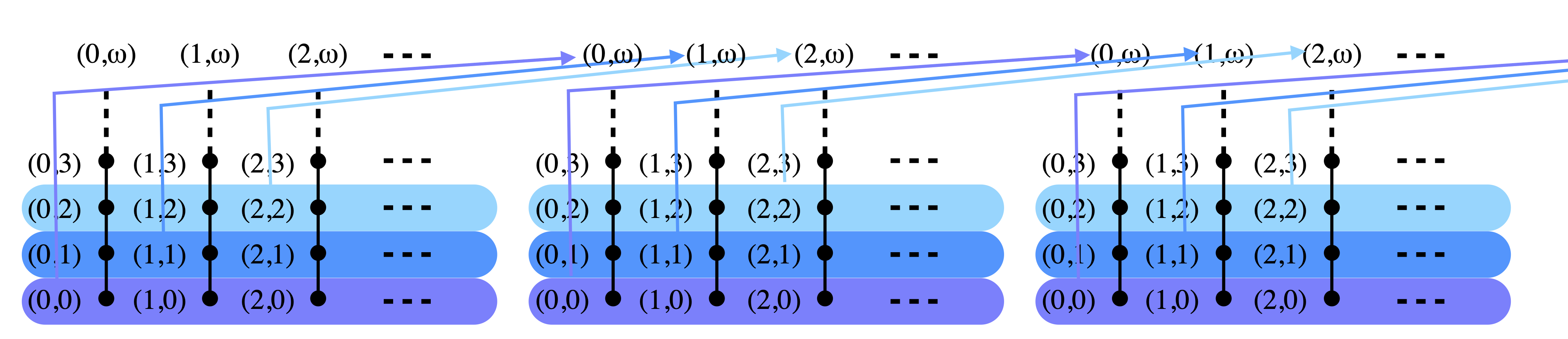
Formally, L is defined as N × N × (N ∪ {ω}), where (i, j, k) ≤ (i’, j’, k’) if and only if: either i=i’ (we stay in the same block), j=j’ (in the same column), and k≤k’ (and we move up, vertically); or i’=i+1 (we move sideways, to the next block to the right), k≤j’ and k’=ω (as in J).
In the sequel, instead of mentioning elements as triples (i, j, k), I will most often say “element (j, k) in block i“.
L is not sober
Following X. Jia, we first show that L is not sober. That is not too hard.
To this end, we simply show that the whole of L itself is irreducible (closed), but not the closure of any point. And this necessitates that we look at the shape of non-empty Scott-open subsets of L. This works exactly as with J, by the way. But please pay attention: we are going to need the following construction exactly three times in this post.
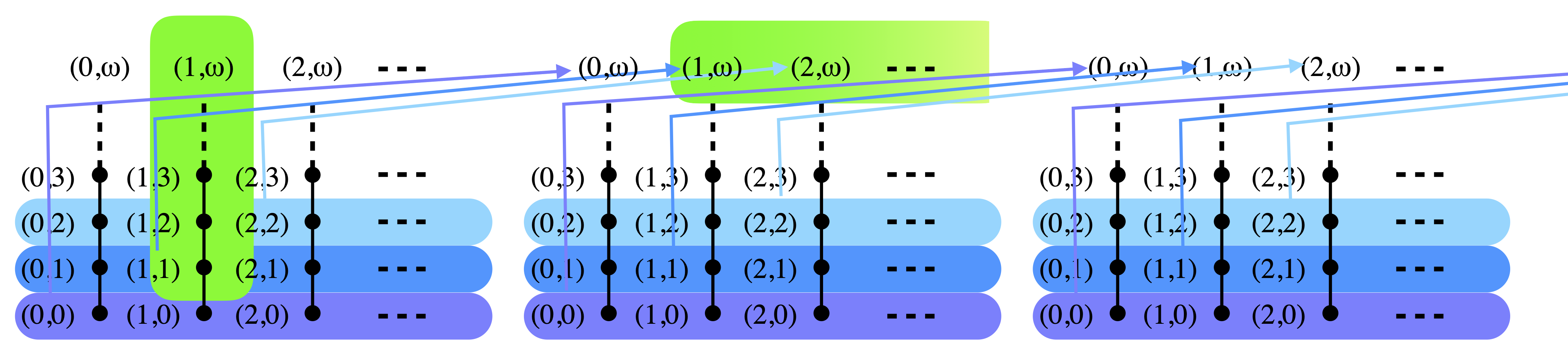
Consider any non-empty Scott-open subset U of L. It contains some maximal element, that is an element (j, ω) in some block i. That element is the directed supremum of the column below it, so some element (j, k) in block i is in U, for some k<ω. Since U is upwards-closed, U must therefore also contain every element (j’, ω) with k≤j’ in the next block, numbered i+1. We repeat the argument: there is a k’<ω such that U contains every element (j”, ω) with k‘≤j” in block i+2. Again: there is a k”<ω such that U contains every element (j”’, ω) with k”≤j”’ in block i+2. And so on.
Hence, if we look at the elements of U that lie on the top row of L, they contain at least the elements in the red region shown below. Explicitly, there is a block (number i in the above argument) such that, in this block and all blocks to its right, U contains all the maximal elements of that block except finitely many.

Now, if U and V are two non-empty open subsets of L, it should be obvious that their red regions intersect (at all but finitely many points in each block sufficiently to the right). This shows that L is irreducible. Of course L is Scott-closed, and not the (downwards-)closure of any point, so L is not sober.
Principal filters in L
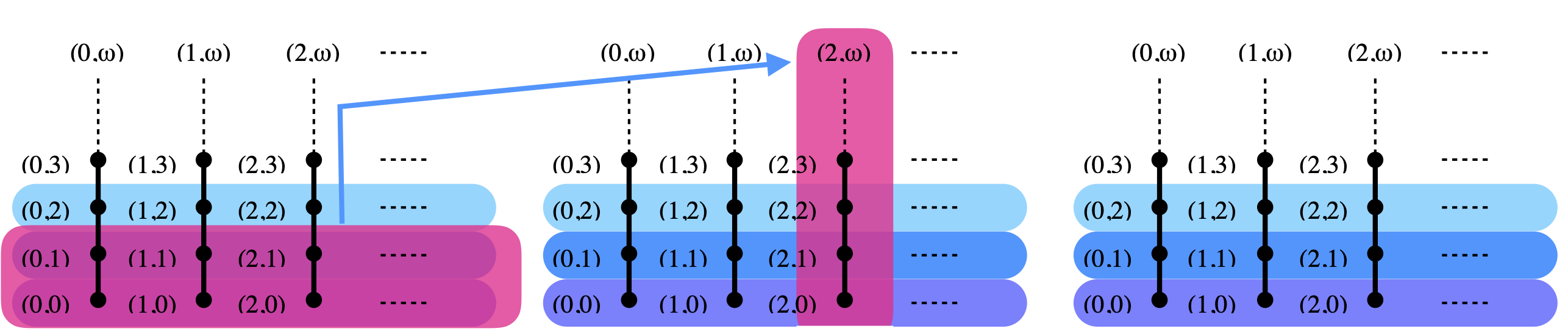
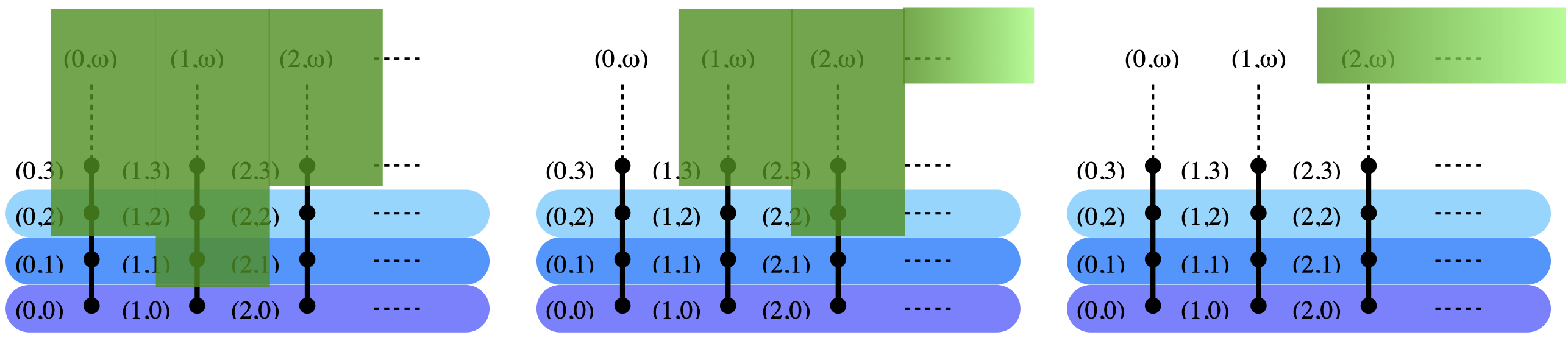
The shape of a principal filter ↑x is very simple. Letting x be (j, k) in block i, either k=ω and then ↑x is just {x}, or k<ω and ↑x consists of just two regions: the vertical column above x, and the points (k, ω), (k+1, ω), (k+2, ω), … in block i+1. Those are the two green regions depicted below (for i=0, x=(1,1)).
Let me call such sets, obtained as the unions of two green regions in neighboring blocks, type I sets. (I will call the sets ↑x = {x} when x is (j, ω) in block i, type III sets below. Please forgive me if the numbering seems awkward to you. I had forgotten that I had already introduced them above.)
Now let us try to understand what ↑x ∩ ↑y looks like. If x≤y or if y≤x, then this is just ↑y, resp. ↑x, so let us assume that x and y are incomparable.
If x and y lie in in the same block i, they must sit in different columns, otherwise they would be comparable. In that case, letting x be (j,k) and y be (j’,k’) (both in block i), ↑x ∩ ↑y is just the set of points {(max(k,k’), ω), (max(k,k’)+1, ω), (max(k,k’)+2, ω), …}, at least if none of x and y are on the top row of L; otherwise ↑x ∩ ↑y is empty. This should be clear from the picture above. Let me call such sets {(max(k,k’), ω), (max(k,k’)+1, ω), (max(k,k’)+2, ω), …} (which are essentially just the second green region from type I sets) type II sets.
If x lies in block i and y lies in block i+1, then ↑x ∩ ↑y contains at most one point of the form (j, ω) in some block. (Similarly if x is in block i+1 and y is in block i.) Let me call type III sets such one-element sets. In all other cases, ↑x ∩ ↑y is empty.

Directed families in L
This study of principal filters will make the examination of directed families easier.
Let me call trivial any directed family which contains its own supremum, namely which has a largest element. We can safely ignore them in the study of closed and open sets. For example, for all natural numbers i and j, the family Dij of points of the form (i, j, k), where k ranges over N but i and j are fixed, is a non-trivial directed family. Here is D12, shown in pink:

Conversely, I claim that:
- Every non-trivial directed family D in L is a chain, that is, a non-empty totally ordered subset.
- Every non-trivial directed family D in L is obtained by selecting infinitely many points from some Dij, plus finitely many points not on the top row of L.
In order to show item 1, for any two points x and y in D, there must be a point z in D above both x and y, hence in ↑x ∩ ↑y. If ↑x ∩ ↑y is of type III, then D is trivial. If ↑x ∩ ↑y is of type II, then notice that all the elements of ↑x ∩ ↑y are pairwise incomparable, so that ↑x ∩ ↑y can contain at most one point of D; hence D is trivial again. Of course ↑x ∩ ↑y cannot be empty. Therefore ↑x ∩ ↑y must be of type I. But the only case where this happens is when x and y are comparable. It follows that D is a chain.
Item 2 follows, or so I claim. Since D is non-trivial, it cannot contain any point that sits on the top row of L, namely of the form (i, j, ω), because those points are all maximal. We fix a point (i, j, k) in D, with k<ω. There are only finitely many points below (i, j, k), namely those under it in the same column. The other points of D must then be in ↑(i, j, k), and since none of them are on the top row, they must all be in the same column j of the same block i. It follows that D consists of a finite number of points, plus points that are all taken from Dij. Since D is non-trivial, it is infinite. Therefore there are infinitely many points of Dij in D.
This is the reason why L is a dcpo: any non-trivial directed family has a supremum, which is the same as the supremum of Dij given by item 2, namely (i, j, ω).
Some Scott-closed subsets of L
In every dcpo, sets of the form ↓x are Scott-closed, hence also any finite union of such sets. Here is the shape that ↓x has when x is not on the top row (in pink):

Here is the shape of ↓x when x is on the top row (in pink again):
But L contains plenty of infinite unions of such sets. For example:
(Closed sets I) Any union of sets ↓x, where each x is on the top row of L, and is taken from a different block, is Scott-closed.
Explicitly, let I be any set of natural numbers. For each i in I, pick a natural number ji. What we claim is that F = ↓{(i, ji, ω) | i ∈ I} is Scott-closed. Indeed, consider any chain Dij included in F. Any element (i, j, k) of Dij, being in F, must be such that i or i+1 is in I. But, if i is not in I, there will be elements (i, j, k) of Dij with k so large that they will get out of F. (In the last picture, i would be the leftmost block. Clearly the infinite chain Dij cannot be included in that block.) Hence i is in I, and then j must be equal to ji. Finally, sup Dij = (i, ji, ω) is in F.
One should be careful. The infinite union of sets of the form ↓x where all the points x are taken from the same block is in general not Scott-closed. For example, the infinite union of the sets ↓(1, j, ω), j ∈ N, is equal to the whole of block 0 expect its top row, plus the whole of block 1. That is not Scott-closed, because it contains the directed sets D0j, j ∈ N, but none of their suprema.
In general, taking the Scott-closure of an infinite union of sets of the form ↓x where all the points x are taken from the same block yields a Scott-closed set of the following form:
(Closed sets II) For all m, n in N, the set Fmn of points (i, j, k) of L such that i<m, or such that i=m and j≥n, is Scott-closed.
Here is what this looks like in pictures:
I will leave it to you to verify that Fmn is Scott-closed. That should be mostly obvious.
We will need a final form of Scott-closed sets.
(Closed sets III) Any union of sets ↓x, where each x is taken from a different column (possibly in the same blocks) and not on the top row, is Scott-closed.
The reason is simpler than in other cases: such a set does not contain any of the non-trivial directed sets Dij. Here is a depiction of a closed sets of that kind.

We are now ready to proceed: we have all the types of Scott-closed sets that we will require below!
The compact saturated subsets of L
What can a compact saturated subset Q of L look like? In order to discover this, we will repeatedly use the following equivalent characterization of compactness: given any filtered family of closed sets, if each of the closed set in the family intersects Q, then the intersection of all the closed sets in the family also intersects Q.
We first note that:
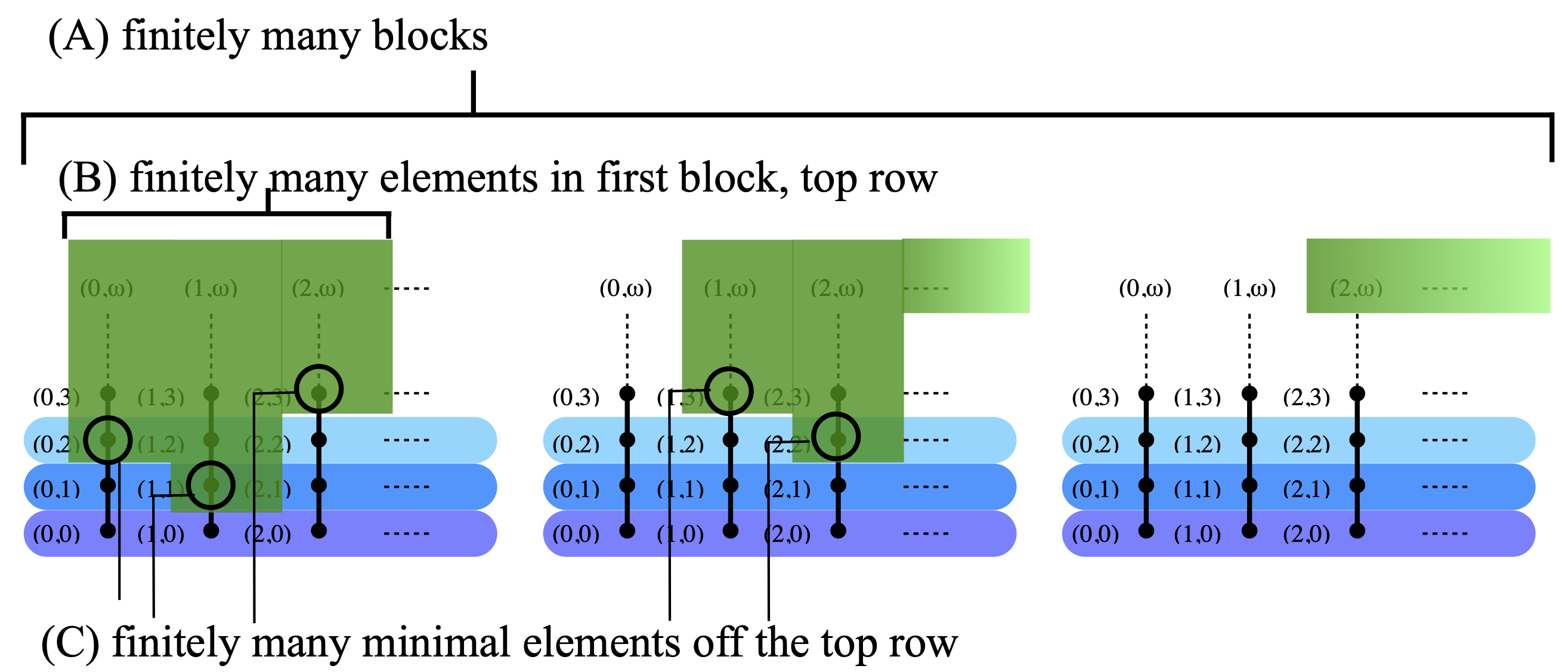
(A) Q is included in a finite union of blocks.
Here is why. Let I be the set of block numbers i such that Q contains an element in block i, and let us imagine that I is infinite. For each such i, there is a point xi in Q, in block i, and on the top row. We pick just one from each block.
For every finite subset I’ of I, the union FI’ of the sets ↓xi where i ranges over I–I’, is Scott-closed. This is an instance of the (Closed sets I) case of the previous section. The family of sets FI’ when I’ varies is filtered (because FI’ and FI” contain FI’ ∪ I”), and each FI’ intersects Q (at any point xi where i ∈ I–I’). Since Q is compact, Q must also intersect the intersection of all those sets FI’.
But that intersection is empty, for the following reason. For each i, ↓xi is contained in the union of the blocks i and i–1 (or just block 0 if i=0). Hence, if we let I’ be the (finite) subset of I consisting of all the natural numbers ≤i+1, FI’ is included in the union of the blocks i+1, i+2, …, and in particular contains no point in block i. Since i is arbitrary, the intersection of the sets FI’ contains no point in no block whatsoever.
Hence Q intersects the intersection of the sets FI’, which is empty. This is a contradiction. Therefore our assumption that I was infinite must be wrong, and this proves (A).
***
Relying on (A), if Q is non-empty, then there is a first block that Q intersects. That is, there is a smallest natural number m such that Q intersects block m, and I will call that block the first block of Q. This leads to our second remark:
(B) If Q is non-empty, then the first block of Q contains only finitely many elements in the top row of L.
In other words, if the first block of Q is block number m, then there is a largest natural number n such that (m, n, ω) is in Q.
In order to show this, we use (Closed sets II). We imagine, for the sake of contradiction, that the set J of natural numbers n such that (m, n, ω) is in Q (for the fixed m denoting the first block) is infinite. Now the Scott-closed sets Fmn of (Closed sets II), with that fixed m, and n ranging over J, all intersect Q, and form a chain, hence a filtered family. Since Q is compact, their intersection also intersects Q. But their intersection contains no element in block m, and all the remaining elements are in blocks that lie to the left of block m, which do not intersect Q either (recall that m is the number of the first block of Q).
***
While (A) and (B) deal with elements of Q that lie on the top row of L, we now look at the elements of Q that are not on the top row of L.
Let Min Q denote the set of minimal elements of Q. It is a general fact that, in any T0 topological space, for every compact saturated subset Q, Q is equal to ↑Min Q. (Quick proof: consider the family F of those closed subsets C that intersect Q. Order that family by reverse inclusion. The compactness of Q implies that F is a dcpo. By Zorn’s Lemma, for every element x of Q, there is a maximal element C of F included in ↓x, namely a minimal closed set included in ↓x that intersects Q. It is an easy exercise to show that C intersects Q at a single point in Min Q.)
Let me also write Minfin Q for the set of minimal points of Q that are not on the top row of L, i.e., {(i, j, k) ∈ Min Q | k < ω}.
Now I claim that:
(C) Minfin Q is finite.
In pictures, imagine that Q is the following green shape:
Minfin Q contains 5 elements in that example: the points (0, 2), (1, 1) and (2, 3) in block 0, and the points (1, 3) and (2, 2) in block 1.
In order to prove (C), we build the closed set F obtained as the union of all the sets ↓x, where x ranges over the points of Minfin Q. This is an instance of (Closed sets III). In the example, this is the set in pink below.
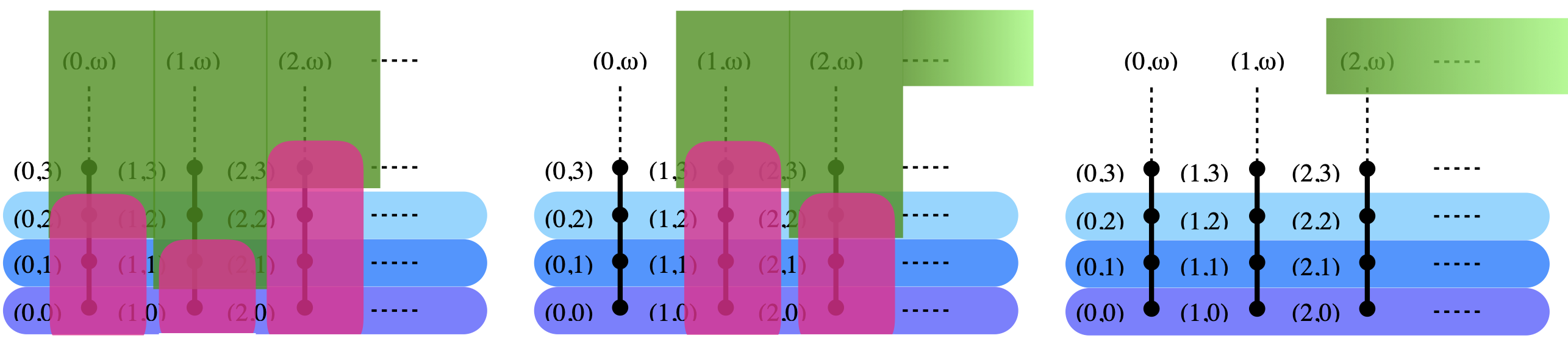
Then, for each finite subset E of Minfin Q, F–E is again Scott-closed: this is again an instance of (Closed sets III). Pictorially, F–E is obtained by simply making finitely many of the pink columns smaller by just one element.
The intersection of all the sets F–E, when E ranges over finite subsets of Minfin Q, does not intersect Q. Again since Q is compact, there is a finite set E of points of Minfin Q such that F–E does not intersect Q. This finite set E must then be exactly Minfin Q, establishing (C).
***
Hence we have obtained that any compact saturated subset Q of L must be of the following shape:
Let us now check the converse: that every upwards-closed set Q that satisfies (A), (B), and (C), is compact in L. This is obvious if Q is empty, so I will assume that Q is non-empty in the sequel; this will simplify condition (B).
We assume that Q is included in a union of Scott-open sets Ui, i ∈ I. The finitely many elements of Minfin Q are covered by finitely many of those sets Ui, and those therefore cover all the elements of Q that are not on the top row.
It therefore remains to show that we can cover the elements of Q that sit on the top row by finitely many of the remaining open sets Ui. This is the only subtle part of the proof, but the core of the argument we are going to play is exactly the argument we have used to understand the shape of Scott-open sets of L.
There is a point (m, j, ω) on the top row, in the first block (number m) of Q. It is in some Ui, and we fix i. Since Ui is Scott-open and (m, j, ω) is the supremum of the chain Dmj, some point (m, j, k) with k<ω is in Ui. Hence every point above it is also in Ui, in particular all the points (m+1, k, ω), (m+1, k+1, ω), (m+1, k+2, ω), … We repeat the argument: for some natural number k’, Ui also contains the points (m+2, k‘, ω), (m+2, k‘+1, ω), … and then also the points (m+3, k”, ω), (m+3, k”+1, ω), … for some k”, and so on. The picture is as shown below: Q is shown in green, and the elements of Ui on the top row are shown in red.

Now we look at the elements of Q that are on the top row. First, there are those that are in Ui (on a red background, above). There may be infinitely many such points (and indeed, look at the top row of block 2 [the third block from the left]), but those are all covered by the single open set Ui. Second, there are the elements on the top row, in Q, but not in Ui. We claim that there are only finitely many points of that second kind. Therefore those can be covered by finitely many of the remaining open sets Uj, and this will finish the proof that Q is compact.
In the picture, the points of that second kind are the points in the green region (Q), against a light orange background (top row), and not against a red background (Ui). [I hope you’re not color-blind, and I’m sorry if you are. I hope you can still follow.] In the first block of Q (the leftmost block, in the picture), there are only finitely many such points by (B). The remaining points all sit in finitely many (non-first) blocks by (A), and outside the red regions. That only leaves finitely many available positions per (non-first) block, and we are done. ☐
L is well-filtered
In order to show that L is well-filtered, we consider a filtered family of compact saturated sets Qi, i ∈ I, we write Q for their intersection, and we assumed that Q is included in some Scott-open set U. We wish to show that some Qi is already included in U. That is obvious if some Qi is empty, so we assume that no Qi is empty in the sequel.
It will be practical to consider the filtered family (Qi)i ∈ I as a monotone net (Qi)i ∈ I, ⊑ of compact saturated sets, where i⊑j if and only if Qi ⊇ Qj. We will show that Qi is included in U for i large enough (recall that this means: there is an index i in I such that for every j in I with i⊑j, Qj is included in U).
We first look at the sets Minfin Qi. By (C), those are finite sets. If i⊑j, then ↑Minfin Qi also contains ↑Minfin Qj. Indeed, every element x of ↑Minfin Qj is above some element y of Minfin Qj. Since y is in Qj, it is also in Qi, hence above some element z of Min Qi. Now z is below y, which is not on the top row, so z is itself in Minfin Qi.
We now use Proposition 5.2.28 of the book (a consequence of Rudin’s Lemma), which tells us that Minfin Qi must be included in U for some i ∈ I. This must also be the case of Minfin Qj for every j in I with i⊑j, so Minfin Qi is included in U for i large enough. This implies that for i large enough, all the points of Qi that are not on the top row must be in U.
For each i ∈ I, let Bi denote set of blocks spanned by the elements of Qi that lie on the top row of L, namely Bi = {m ∈ N | for some n ∈ N, (m, n, ω) is in Qi}. By (A), those are finite sets. Moreover, if i⊑j, then Bi contains Bj. Hence, the sets Bi form a filtered family of finite sets. It is then easy to see that, for i large enough, Bi is constant.
In particulier, for i large enough, all the sets Qi have the same first block, say number m. By (B), the set Ai of numbers n such that (m, n, ω) is in Qi is finite. Moreover, if i⊑j, then Ai contains Aj. This is again a filtered family of finite sets, so for i large enough, Ai is constant. Let us call that constant value A.
It follows that all the points (m, n, ω) with n in A are in Q. Hence they are all in U. We play the same game as we have already done before: picking one of these points, we can find a point (m, n, k) with n in A and k<ω inside U; then all the points (m+1, k, ω), (m+1, k+1, ω), (m+1, k+2, ω), … are also in U; for some natural number k’, U also contains the points (m+2, k‘, ω), (m+2, k‘+1, ω), … and then also the points (m+3, k”, ω), (m+3, k”+1, ω), … for some k”, and so on. The picture is the same as before, see below, where Qi (for i so large that its first block is block number m and that Ai=A) is shown in green, and the points of U on the top row are shown in red.

Let Ci denote the set of points of Qi that are on the top row of L, but outside U (not in the red region). Ci is a union, over finitely many blocks (by (A)) of finite sets (because each red band covers all the points from the top row of the corresponding block except finitely many; except in the first block, where Ci contains only finitely many points anyway, by (B)). Again the sets Ci form a filtered family of finite sets, hence are constant for i large enough. Let us call C that constant set.
Clearly, C is also the set of points of Q that are on the top row of L, but outside U. Since Q is included in U, C is empty.
Hence we have proved: for i large enough, the set Ci of points of Qi that are on the top row of L, but outside U, is empty. In other words, for i large enough, all the points of Qi on the top row of L are in U.
Since, as we recall, for i large enough, all the points of Qi that are not on the top row of L are also in U, the whole of Qi is included in U.
This finishes to show that L is well-filtered.
A final word
I hope to have explained X. Jia’s example clearly enough. Although the example by itself is simple, showing that it is indeed a non-sober, well-filtered dcpo is definitely non-trivial.
I once thought that one could simplify the proof of well-filteredness of L by using the results by Jimmie Lawson and Xiaoyong Xi mentioned in this previous post. For example, one might hope to show that Property (*) mentioned there holds in L, namely that every principal filter ↑x is Lawson-compact in L. That would immediately imply that L is well-filtered. However, Property (*) fails. I will let you do that as an exercise, using the shapes of intersections of principal filters (Types I, II, and III): just show that there are families of principal filters whose intersection is empty, but such that the intersection of any finite subfamily is non-empty; as a hint, Type II sets are useful here.
Hence, I am sorry to have let you suffer studying L, but that seems to have been necessary!
A final remark: recall that, by a(nother) theorem due to Jimmie Lawson and Xiaoyong Xi, every core-compact well-filtered T0 space is sober. It follows that L, just like Hui Kou’s original example [2] or Xi and Zhao’s example [5], is not core-compact.
- Peter T. Johnstone. Scott is not always sober. Lecture Notes in Mathematics 871, Springer-Verlag, Berlin and New York, pages 282-283, 1981.
- Hui Kou. Uk-admitting dcpo’s need not be sober. In K. Keimel, G.- Q. Zhang, Y.-M. Liu, and Y.-X. Chen, editors, Domain and Processes, volume 1 of Semantic Structures in Computation, pages 41–50. Kluwer Academic Publishers, 2001.
- Xiaodong Jia. Meet-Continuity and Locally Compact Sober Spaces. PhD thesis, University of Birmingham, 2018.
- Xiaoyong Xi and Dongsheng Zhao. Well-filtered spaces and their dcpo models. Mathematical Structures in Computer Science, Volume 27, Special Issue 4 (Symposium on Domain Theory (ISDT 2013)), May 2017, pp. 507-515.
- Dongsheng Zhao, Xiaoyong Xi, and Yixiang Chen. A new dcpo whose Scott topology is well-filtered but not sober. Topology and its Applications. Volume 252, 1 February 2019, Pages 97-102.

— Jean Goubault-Larrecq (March 20th, 2020)
