My purpose today is to talk about the characterization of certain properties of posets and dcpos by so-called forbidden substructures. Although this is a pretty old theme, Xiaodong Jia really managed to make it shine in his PhD thesis [2].
Here is a trivial example of forbidden substructure. Consider a poset X, and recall that X has the ascending chain condition (a.k.a., the ACC, see Proposition 9.7.6 in the book) if and only if every monotone sequence eventually stabilizes. (Equivalently: there is no infinite strictly ascending sequence in X.) Another way of saying that is that X has the ACC if and only if you cannot find a copy of the poset N of natural numbers inside X, or, in formal terms, there is no order-embedding of N into X. Here N is the forbidden substructure.
Before we come back to order theory, let me mention some exciting examples of forbidden substructures in graph theory. I will then come back to order theory, briefly, and then to domain theory.
Forbidden substructures in graph theory
There is a famous theorem, due to Kuratowski, which says that a graph is planar if and only if you cannot find any copy of K5 (the complete graph on 5 vertices) or of K3,3 (the complete bipartite graph on 3+3 vertices) in it. I have deliberately removed some of the details (see the Wikipedia page), and in particular I have not said what “in it” means (see later), that is, what the substructure relation is. (The substructure relation was the existence of an order-embedding in our example about the ACC. Here, one requires a certain notion of graph embedding, and there are several.)
What I want to stress is that planarity is characterized by forbidden substructures again: here K5 and K3,3 are the substructures that are forbidden.
In graph theory, the celebrated Robertson-Seymour theorem states that any minor-closed (i.e., downwards-closed with respect to the so-called minor embedding relation) family F of graphs can be characterized by finitely many forbidden structures: there are finitely many graphs G1, …, Gn such that F is the class of graphs that do not contain any Gi as a minor. In the case of planarity, n=2 and the two forbidden graphs are K5 and K3,3. (That is Wagner’s theorem, not Kuratowski’s, in that case, if one wants to be precise. I will not define what a minor is.) But the theorem applies to any minor-closed family, and since the proof is not constructive, there are minor-closed families of graphs for which noone knows of any finite class of forbidden minors—although we know that they must exist. That has weird implications in computer science: because testing for minors can be done in polynomial time, there are polynomial time algorithms to test any minor-closed property of graphs — however there are several cases where we do not know what these algorithms are: we have to check for minors, but which ones?
Forbidden structures in order theory
I have already mentioned how one could characterize posets with the ACC by N as a forbidden substructure. Here “substructure of” means “poset that order-embeds into”.
There are many order-theoretic concepts that one can characterize similarly. For example, a well-founded poset is one that has Z– as forbidden substructure (the set of negative integers, with the usual ordering). A poset that is well-quasi-ordered is the same thing as a poset that is well-founded and has no infinite antichain (Proposition 9.7.17, item 4, in the book), hence is the same thing as a poset in which neither Z– nor N= order-embeds, where N= is the set of natural numbers with = as ordering.
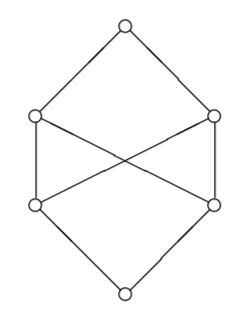
Here is a more interesting one. Recall that a lattice L is distributive if and only if u ⋀ sup(v, w) = sup (u ⋀ v, u ⋀ w) for all u, v, w in L, or equivalently u ⋀ sup(v, w) ≤ sup (u ⋀ v, u ⋀ w) since the converse inclusion always holds. Distributivity can be characterized by the forbidden substructures N5 or M3 (see Figure 8.1 in the book, or below). This is well-known, but the way it is proved is interesting, and typical. (Correction, October 18th, 2022: the two lattices are forbidden, not in the sense that they should not order-embed, but that they should not embed through an order-embedding that preserves binary sups and binary infs.)
Proposition. L is not distributive if and only if N5 or M3 order-embeds in L. (Correction, October 18th, 2022: lattice-embeds, not order-embeds: the embedding must also preserve both binary sups and binary infs.)
Here is a proof of the interesting direction. Assume that L is not distributive. L must therefore contain three points a, b, and c such that: (*) b ⋀ sup(a, c) ≰ sup (b ⋀ a, b ⋀ c).
Case 1. If b and c are comparable, say b ≥ c, then (*) simplifies to: (**) b ⋀ sup(a, c) ≰ sup (b ⋀ a, c). If b were equal to c, then that would simplify further to c≰ sup (c ⋀ a, c), which is absurd, so b>c. Similarly, a≥c together with (**) would imply b ⋀ a ≰ sup (b ⋀ a, c), and a≤b would imply b ⋀ sup(a, c) ≰ sup (a, c), both of which are absurd. So a must be incomparable with both b and c. Since L is a lattice, we must also find a point ⊤=sup(a,b) and a point ⊥=a ⋀ c. Therefore L must contain the non-distributive lattice N5 as order-embedded poset.
Case 2. b and c are incomparable. If a≥c then (*) simplifies to b ⋀ a ≰ sup (b ⋀ a, b ⋀ c), which is impossible. If a≤c then (*) simplifies to b ⋀ c ≰ sup (b ⋀ a, b ⋀ c), which is impossible again. So a and c are incomparable. If a≥b then (*) simplifies to b ≰ b ⋀ c. If a<b then we recognize a copy of N5 again, with b atop a, c on the side, plus a top element and a bottom element. Otherwise, a and b are incomparable, and together with a top and a bottom obtained as sup(a,b,c) and a ⋀ b ⋀ c respectively, one recognizes a copy of M3. ☐
Forbidden substructures in dcpos.
I do not know exactly who was the first to recognize the importance of forbidden structures in domain theory. I had the impression that that should be Achim Jung, but I have found only a few traces of the idea in his PhD thesis [1], and I would have expected to see more of it there.
There is at least one explicit occurrence of the technique there. In Proposition 4.22, page 98, Achim shows that a pointed continuous dcpo with property m is a continuous L-domain if and only if it does not contain a certain dcpo X⊥⊤ as a retract (see below for X⊥⊤; the picture is taken straight from Achim’s PhD thesis).
And there is the new feature: by a substructure A of B, we no longer mean that A order-embeds into B, rather that A is a retract of B.
That is a strictly stronger property, and this is exactly the kind that we need in the study of function spaces in domain theory. The reason is that if X embeds as a retract inside X’, and if Y embeds as a retract inside Y’, then the continuous function space [X → Y] embeds as a retract inside [X’ → Y’]. A similar property would fail with mere order-embeddings.
There are several properties of (certain classes of) dcpos that one can characterize by forbidden retracts. For example, improving upon the result we have just mentioned, Xi and Yang show [3] that a bicomplete dcpo (a poset X is bicomplete if and only if both X and Xop are dcpos) is a pointed L-domain if and only if it does not contain any of the following dcpos as retract: X⊥⊤, the two-element antichain {a, b}, and the three-element poset {a, b, ⊤} (with ⊤ above a and b, and a and b incomparable).
Meet-continuity
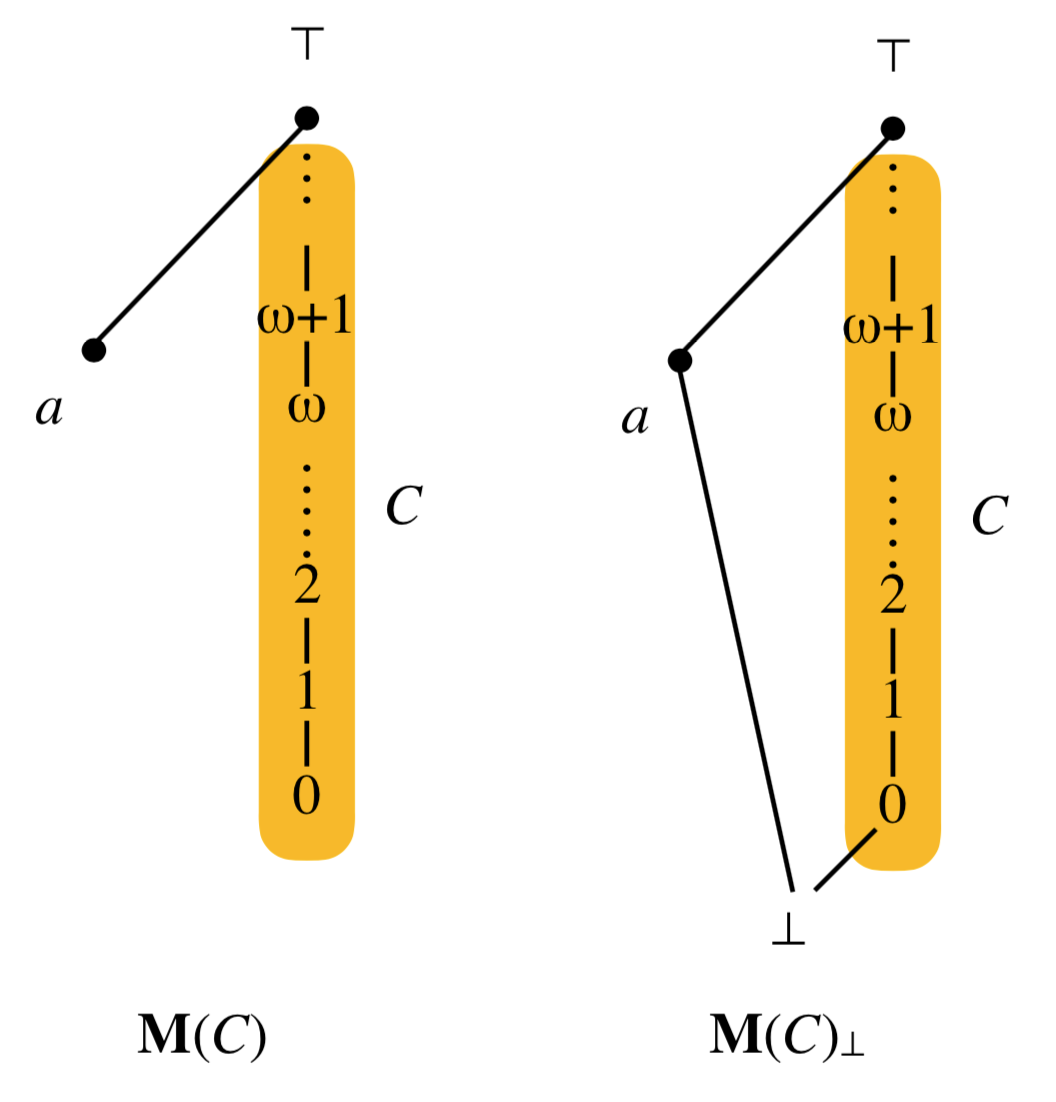
I have talked about meet-continuous dcpos last month. Here is an example of a non-meet-continuous dcpo. We take any well-founded chain C without a top element. Call its least element 0. We add a fresh element a on the side, that is, incomparable with every element of C, and a fresh element ⊤ above a and all elements of C. Call M(C) the resulting dcpo. This is the dcpo shown below, left. Note that the chain C need not be just a copy of the natural numbers: we allow any ordinal here.
Let us verify that M(C) is not meet-continuous. We use Kou, Liu and Luo’s definition [4]: a dcpo is meet-continuous if and only if for every directed family D and every y ≤ sup D, y ∈ cl (↓D ∩ ↓y). For D, we take the chain C itself, so sup D = ⊤. We take y=a, so y ≤ sup D indeed, but ↓D ∩ ↓y is empty, so certainly y cannot be in cl (↓D ∩ ↓y).
If we add a fresh element ⊥ below all the elements of M(C), we obtain another dcpo M(C)⊥ (see above, right). Then M(C)⊥ is a lattice, and we can check that M(C)⊥ is not meet-continuous either by simply checking that the map a ⋀ _ is not Scott-continuous: a ⋀ sup C = a ⋀ ⊤ = a, but supc ∈ C (a ⋀ c) = 0.
One of the nice results in Xiaodong Jia‘s PhD thesis is that those two objects M(C) and M(C)⊥ are exactly the structures that one has to forbid as a retract to define meet-continuous dcpos.
Theorem ([2], Theorem 3.3.11.) Let X be a dcpo. Then X is meet-continuous if and only if it admits neither M(C) nor M(C)⊥ as retract, for any well-founded chain C.
The idea of the proof is as follows. If X contains M(C) or M(C)⊥ as a retract, then X cannot be meet-continuous, essentially by replaying the argument we have used for M(C). In the converse direction, assume that X is not meet-continuous. Then there is a directed family D and a point a such that a ≤ sup D but a is not in cl (↓D ∩ ↓a).
The core of the proof consists in showing that we can replace D by a well-founded chain C. In other words, we would like to show that there is a well-founded chain C such that a ≤ sup C but a is not in cl (↓C ∩ ↓a). We shall do that later.
For now, imagine we have such an a and C. That gives us a copy of M(C) order-embedded in X, together with sup C, which we label ⊤ (that need not be the top element of X, though, even if there is one).
If ↓C ∩ ↓a is empty, then M(C) occurs as a retract of X: the retraction maps every element below a to a, every element below some element c of C but not below a to the least such c (which is defined since C is well-founded), and all other elements to ⊤. (Hmm… you also have to show that the inclusion of M(C) inside X is Scott-continuous. That only works if C is limit-embedded in X, as X. Jia calls it. Let me ignore this point. This only adds minor technical difficulties to the whole construction.)
If ↓C ∩ ↓a is not empty, then M(C)⊥ is a retract of X. This is a bit more complicated. We pick b from ↓C ∩ ↓a, then there is a point c in C such that b≤c, and we take the least one. Now we remove c and everything below it from C, and define a retraction by mapping every element of cl (↓C ∩ ↓a) to ⊥; all other elements are mapped to elements of M(C) exactly as in the case where ↓C ∩ ↓a is empty.
Fine, but we still have something to do! We would like to show that if X is not meet-continuous, then there is a well-founded chain C such that a ≤ sup C but a is not in cl (↓C ∩ ↓a). (In fact, a limit-embedded one.)
This is (half of) Theorem 3.3.8 in Xiaodong Jia’s PhD thesis, and the key is Iwamura’s Lemma.
Find a directed family D of smallest cardinality |D| (ordinals are well-founded) such that there is a point a such that a ≤ sup D but a is not in cl (↓D ∩ ↓a). D cannot be finite, since then D would have a largest element d, which would be above a, and cl (↓D ∩ ↓a) would be equal to ↓d. By Iwamura’s Lemma, we can then write D as the union of a chain of directed subsets Dα, indexed by ordinals α<|D|, such that:
- |Dα| < |D|
- if α<β then Dα is included in Dβ
Let C be the chain consisting of the points sup Dα, α<|D|. (You can make it limit-embedded by adding the suprema in X of all subchains of C that have an upper bound in C, but I don’t want to make the exposition too complicated, hence I will ignore this point.)
We claim that a≤sup C (indeed, since sup C=sup D), and that a is not in cl (↓C ∩ ↓a). For that, we reason by contradiction. Assume that a is in cl (↓C ∩ ↓a). Let U be the complement of cl (↓D ∩ ↓a), and notice that this is an open neighborhood U of a—recall that a is not in cl (↓D ∩ ↓a). Since U intersects cl (↓C ∩ ↓a) (at a), it also intersects ↓C ∩ ↓a, say at d. This means that d is in U, below some sup Dα, and below a. Because of the fact that |D| was chosen minimal, and since d≤sup Dα, d is in cl (↓Dα ∩ ↓d). Hence U intersects cl (↓Dα ∩ ↓d), hence also ↓Dα ∩ ↓d, hence also the larger set ↓D ∩ ↓d, which is itself included in ↓D ∩ ↓a since d≤a. But that is impossible, in the light of how we defined U. ☐
All CCCs of quasicontinuous domains must consist of continuous domains
That is just one step in X. Jia’s PhD thesis leading to the following wonderful result (Theorem 3.4.3 in [2]):
Any full Cartesian-closed subcategory of the category of dcpos whose objects are all quasi-continuous must in fact consist of continuous dcpos only.
(And therefore, of continuous L-domains, or of FS-domains, by Achim Jung’s celebrated classification result — at least in the pointed case.)
Here is the argument. Assume that CCC contained a quasi-continuous, non-continuous dcpo X. Since quasi-continuity+meet-continuity=continuity (a result by Hui Kou of which Weng Kin Ho had given an improved proof of, and which was the subject of last month’s post), X cannot be meet-continuous.
Now we know that X must contain M(C) nor M(C)⊥ as retract, for some well-founded chain C. Let L=M(C) or M(C)⊥, depending on the case. Xiaodong Jia shows that [L → L] is not locally compact [2, Proposition 3.4.1]. This is tricky, but doable because of the restricted shape that L has. He also shows that every core-compact dcpo in which every non-empty family has a supremum must be sober, hence locally compact [2, Theorem 2.5.8]. Due to the special form of L, that result applies to [L → L]. If it were core-compact, it would then be locally compact, which it is not. Since [L → L] is a retract of [X → X] , and core-compactness is inherited by retracts, [X → X] cannot be core-compact either, and that contradicts the fact that it lives in a category of quasi-continuous dcpos.
- Achim Jung. Cartesian Closed Categories of Domains. PhD thesis, Technische Universität Darmstadt, 1988.
- Xiaodong Jia. Meet-Continuity and Locally Compact Sober Spaces. PhD thesis, University of Birmingham, 2018.
- Xiaoyong Xi and Jinbo Yang. Coincidence of the Isbell and Scott topologies on Domain Function Spaces. Topology and its Applications, 164(2014), 197-206.
-
Ying-Ming Liu, and Mao-Kang Luo. On Meet-Continuous Dcpos. In G. Zhang, J. Lawson, Y. Liu, and M. Luo, editors, Domain Theory, Logic and Computation, volume 3 of Semantic Structures in Computation, pages 117–135. Springer Netherlands, 2003.
— Jean Goubault-Larrecq (March 19th, 2018)![]()