In my first post on ideal domains, I thought I would be able to extend Keye Martin’s result from metric to quasi-metric spaces. Of course, the set Max Y of maximal elements of a dcpo Y cannot yield an arbitrary quasi-metric space X, since Max Y is always a T1 space. I think I am on my way to obtain that generalization, but let us not go too fast.
Let us ponder at other ways to look at what an ideal domain really is.
In an ideal domain Y, X = Max Y occurs as the set-theoretic difference Y — Y0, where Y0 is the set of finite elements of Y. As for any algebraic domain, Y is then isomorphic to the ideal completion I(Y0) of Y0 (Exercise 5.1.47 in the book).
This leads to the following question: what topological spaces arise as ideal completion remainders, that is, as the difference I(P) — P for some poset P?
A few years ago, I would have thought the question was silly. However, it arises here and there, possibly under slightly different forms. Let me start with a curious result, due to Péquignot and Carroy [4].
Wqos, bqos and ideal completion remainders
A well-quasi-order (wqo, for short) is a quasi-ordered set P which has no infinite strictly descending chain and no infinite antichain. This is, by the way, a special case of a Noetherian space (see Proposition 9.7.17 in the book). I will assume that P is actually a poset. That does not do much harm, since otherwise we may quotient P by the equivalence relation induced by the quasi-ordering.
There is a much stronger notion, due to Nash-Williams, and called better quasi-ordering, or bqo. The definition is pretty complex. Let me just say that every bqo is wqo, that every total well-founded order is bqo, that every naturally occurring wqo is in fact bqo (to the exception of the graph minor relation, which is wqo by a celebrated result of Robertson and Seymour, but not known to be bqo), and that being bqo is preserved by many constructions.
The ideal completion I(P) of P is in general not a wqo. In fact, it is a wqo if and only if P is what is known as an ω2-wqo, a notion stronger than wqo but weaker than bqo; equivalently, if and only if P does not embed the so-called Rado counter-example: see Exercise 9.7.25 in the book.
What Yann Péquignot and Raphaël Carroy prove [4] is that the ideal completion remainder I(P) — P of a wqo P is bqo if and only if P is already a bqo.
I am not going to expand on this result right now. It is a nifty result, and one that shows that ideal completion remainders do sometimes crop up.
Let me return to the original question: what spaces are the ideal completion remainders of posets?
Sobrification remainders
A very similar question was studied by Rudolf-Eberhard Hoffmann [2]. A sobrification remainder is a topological space that arises as the difference S(Z) — Z for some T0 topological space Z. Here S is sobrification, and the analogy comes from the fact that if P is a poset with its Alexandroff topology, then S(P)=I(P) (Fact 8.2.49 in the book).
If we agree to replace ideal completion by sobrification, then R.-E. Hoffmann solved the problem completely:
Theorem [2, Theorem 1.6]. The sobrification remainders are exactly the T0 topological spaces.
Proof. Clearly, every sobrification remainder is T0. Conversely, let X be an arbitrary T0 topological space. Let N be the poset of natural numbers, in its usual ordering. S(N)=I(N) is just N U {+∞}. Let Y be the space (S(N) x S(X)) — ({+∞} x X), seen as a subspace of S(N) x S(X). We show that S(Y) is isomorphic to S(N) x S(X), from which it will follow that S(Y)—Y is isomorphic to X.
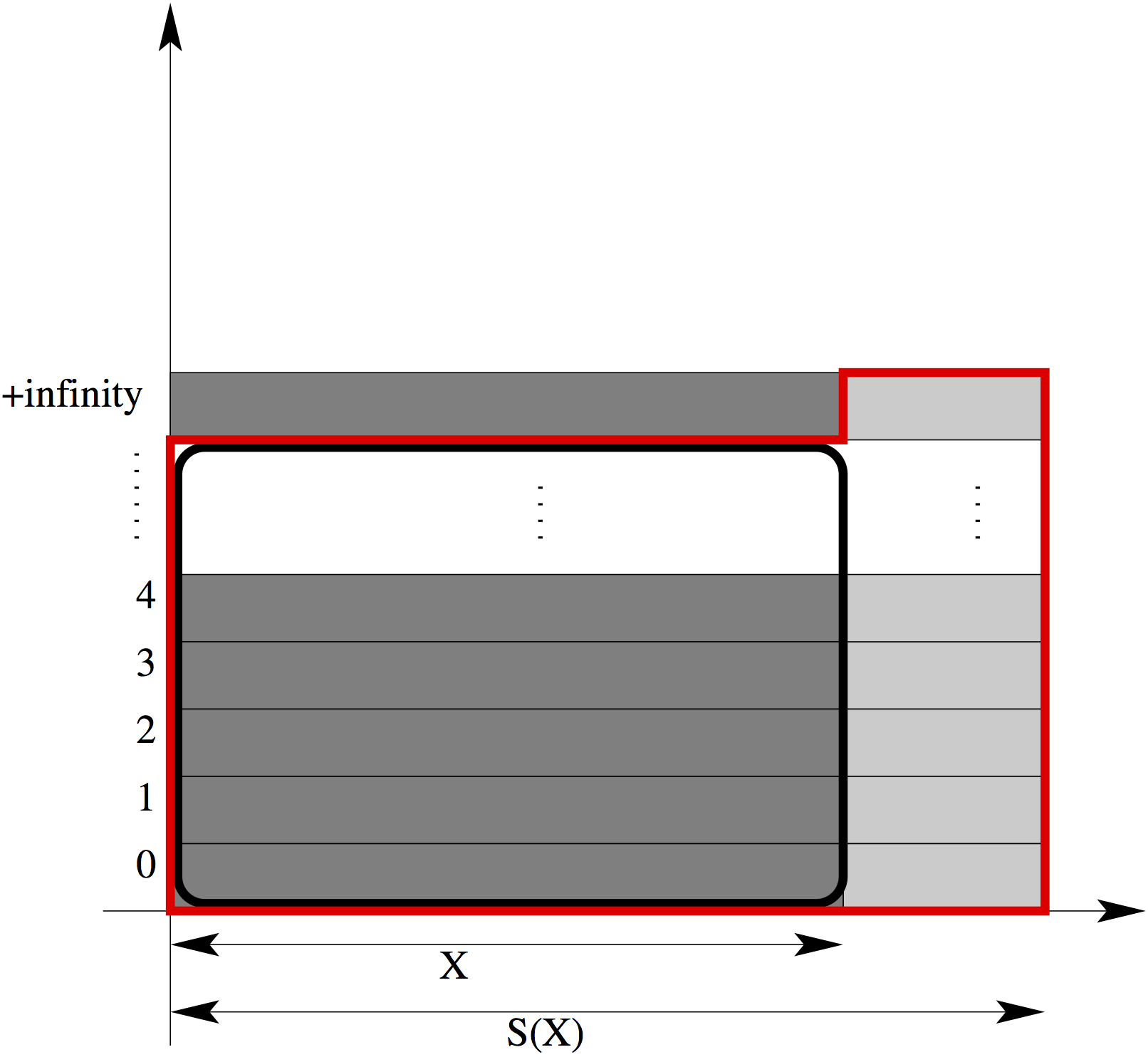
Hoffmann does it via a detour through the Skula topology, but there is a simpler (and more categorical) way. This is pictured below: take S(X), and represent it as a horizontal slab; make infinitely many copies of this slab, all stacked up at levels 0, 1, 2, 3, 4, …, plus a new level at +infinity. Y is the space delimited by the red boundary. We shall show that S(Y) is equal to the outer square, and this will be because it will be contain the sobrification of the smaller rounded square N x X, and is contained in the same sobrification already (the outer square). Now S(Y)—Y will be the copy of X at level +infty, the one that is not surrounded by any red.
Let us do that formally. First, recall that S(N) x S(X) is isomorphic to S(N x X) (Theorem 8.4.8 in the book). Since N x X is T0, the map ηSX : N x X → S(N x X), which sends every element to its closure, is an embedding (Theorem 8.2.44). This yields an embedding of N x X into S(N) x S(X), which we also write as ηSX, and which maps (n, x) to (n, ↓x). No element (n, ↓x) is in {+∞} x X, so ηSX, also defines an embedding of N x X into Y.
There is also a subspace embedding j of Y into S(N) x S(X) = S(N x X). We now use the fact that the S functor preserves embeddings (Lemma 8.4.11): S(ηSX) is an embedding of S(N x X) into S(Y), and S(j) is an embedding of S(Y) into S(S(N x X)) ≅ S(N x X). Their composition is easily seen to be the identity map, so they are inverse of each other. In particular, S(Y) is isomorphic to S(N x X), and we are done. ☐
Hoffmann’s construction does not build the space Y as a poset, hence that does not the answer the question of which spaces are ideal completion remainders. However, we do have partial answers.
Quasi-Polish spaces
I have already mentioned quasi-Polish spaces [3]. One of the things mentioned in that paper, and which I have not cited yet, is the following: the spaces that are homeomorphic to the subspace of non-finite elements of an ω-algebraic dcpo are exactly the quasi-Polish spaces.
A dcpo is ω-algebraic if and only if it is algebraic and has a countable basis, equivalently, it has countably many finite elements. In other words, an ω-algebraic dcpo is the same thing as the ideal completion of a countable poset. Let us reformulate:
Theorem (de Brecht). The ideal completion remainders of countable posets are (up to homeomorphism) exactly the quasi-Polish spaces.
This is Theorem 53, Item 3, of [3]. I will give you an idea of Matthew de Brecht’s proof below. Before that, let me mention that this allows Matthew de Brecht to characterize completely the spaces that have an ω-ideal model, that is, an ideal model with only countably many finite elements:
Corollary (de Brecht, Corollary 54). The spaces with an ω-ideal model are exactly the T1 quasi-Polish spaces.
Recall that a space is quasi-Polish if and only if it is obtained from a second-countable Smyth-complete quasi-metric space X, d, forgetting about the quasi-metric d and keeping the topology.
We first imitate Alexandroff’s Theorem (Theorem 7.7.11 in the book). That says that the Polish (not quasi-Polish) spaces are, up to homeomorphism, the Gδ subsets of the Hilbert cube [0, 1]N. Matthew de Brecht shows instead that the quasi-Polish spaces are the Π02 subsets of the dcpo P(N) of all subsets of N (ordered under inclusion). Standardly, that is, in metric spaces, “Π02” is synonymous with “Gδ“, but, as discovered by Victor Selivanov earlier on, it is more meaningful to define “Π02” differently in non-T2 spaces. (“Π02” and “Gδ” will still be equivalent properties on T2 spaces.)
Accordingly, a subset A of a topological space X is called Π02 if and only if there is a countable family of pairs of opens Ui, Vi, i ∈ N, such that, for every x ∈ X, x is in A if and only if for every i ∈ N, x ∈ Ui ⇒ x ∈ Vi.
If X, d is second-countable, then we can embed X into P(N) in the usual way: index a countable base (Ui)i ∈ N by natural numbers, and map each point x of X to the collection of indices i such that x ∈ Ui. When X, d is also Smyth-complete, this is really an embedding, so we can see X as a subspace of P(N). Using the strong Choquet game, M. de Brecht shows that a subspace of a quasi-Polish space is quasi-Polish if and only if it is Π02 (if and only if it is convergence Choquet complete). Every ω-continuous dcpo, in particular P(N), is quasi-Polish, so X arises as a Π02 subset of P(N).
This shows that every quasi-Polish space X embeds as a Π02 subset of P(N). There is a countable family of pairs of opens Ui, Vi, i ∈ N, in P(N) such that, for every a ∈ P(N), a is in X if and only if for every i ∈ N, a ∈ Ui ⇒ a ∈ Vi. Let F be the set of finite subsets E of P(N) such that E is contained in some x ∈ X (or rather, in the element of P(N) that x is mapped to by the embedding). Matthew de Brecht builds a poset P = F x N, with a specific ordering: (E, n) is below (E‘, n‘) if and only if either they are equal, or E ⊆ E‘ and n<n‘ and for every i≤n such that E ⊆ Ui, E’ ⊆ Ui. He then shows that X embeds in I(P) through the map that sends x to the set of all pairs (E, n) such that E is included in x. Moreover, that set is a non-principal ideal, and that shows that X embeds into the ideal completion remainder I(P) — P. Note also that P is countable.
We now know one direction of the theorem: every quasi-Polish space embeds into the ideal completion remainder of a countable poset.
For the converse direction… let us pause for a minute. Matthew observes that every second-countable, locally compact sober space X is quasi-Polish [3, Theorem 44], and we shall use that. That result should be compared with the fact that every second-countable, locally compact T3 space is Polish (Corollary 8.3.28 in the book). Matthew proves that theorem by embedding X into P(N) using the countable base, and then characterizing the image of the embedding as an explicitly constructed Π02 subset. P(N) is quasi-Polish, either by realizing it is a countable product of copies of Sierpiński space, or directly, by defining the quasi-metric d by d(A, B) = 1/2n, where n is the least natural number that is in A but not in B, and 0 if A ⊆ B. Since every Π02 subset of a quasi-Polish space is quasi-Polish, the second-countable, locally compact sober space X is quasi-Polish.
We can now finish. Let P be a countable poset. I(P) is ω-algebraic, hence ω-continuous, hence second-countable (by Norberg’s Lemma 7.7.13 in the book), and continuous hence locally compact sober. Therefore, as we have just seen, I(P) is quasi-Polish. Now enumerate the (countably many) finite points pi of P. Ui = ↑pi of P (the upward-closure of pi in I(P)) is open, because pi is finite, and Vi = Ui — {pi}. The points x of I(P) such that for every i ∈ N, x ∈ Ui ⇒ x ∈ Vi. are exactly the points of I(P) that are not in P, and, by definition, they form a Π02 subset of the quasi-Polish space I(P). In other words, the ideal completion remainder I(P) — P is quasi-Polish.
That finishes our tour of Matthew de Brecht’s proof that the ideal completion remainders of countable posets are exactly the quasi-Polish spaces.
Next time…
Next time, I may explain how we can generalize the first part of the proof, and obtain ideal completion remainders (not necessarily of countable posets) from continuous Yoneda-complete quasi-metric spaces. That is, if all goes well: I am not completely sure that everything works. If that works, we shall see that those ideal completion remainders can even be made to resemble ideal domains, in a sense that I will make precise.
(Note added, Dec 23rd, 2019. It seems that the bibliographic references were absent. Putting them back:)
- Keye Martin. Ideal models of spaces. Theoretical Computer Science, Volume 305, Issues 1–3, 18 August 2003, pages 277–297.
- Rudolf-Eberhard Hoffmann. On the Sobrification Remainder sX–X. Pacific Journal of Mathematics, 83(1), 145–156, 1979.
- Matthew de Brecht. Quasi-Polish spaces. Annals of Pure and Applied Logic, Volume 164, Issue 3, March 2013, pages 356-381.
- Raphaël Carroy and Yann Péquignot. From Well to Better, the Space of Ideals. Fundamenta Mathematicae, 2014, 227 (3), pages 247-270.
— Jean Goubault-Larrecq (January 27th, 2016)![]()