In his famous paper on the classification of continuous domains [1], Achim Jung showed that there were exactly two maximal categories of continuous dcpos: the L-domains, and the FS-domains. He invented the latter for the occasion, and they are the subject of exercises 9.6.25 through 9.6.32 in the book.
Every RB-domain is known to be an FS-domain, and we know that all algebraic FS-domains are RB-domains, in fact bifinite domains. The biggest conjecture about FS-domains is whether there is any FS-domain at all that is not an RB-domain. After 28 years, this is still an open problem.
In [1], Achim finishes section 4 by “a concrete example of an FS-domain”, suggested to him by Jimmie Lawson. This is meant to be a likely candidate of a non-RB FS-domain… but we are lacking tools to show that something is not an RB-domain.
FS-domains
In a dcpo X, a Scott-continuous function f : X → X is finitely separated from the identity if and only if there is a finite subset M of X such that, for every x ∈ X, there is an element m ∈ M such that f(x) ≤ m ≤ x.
An FS-domain is a dcpo X with a directed family (fi)i ∈ I of Scott-continuous maps, finitely separated from the identity, and whose pointwise supremum is the identity map.
For example, on [0, 1] with its usual ordering, for every ε>0, the map x ↦ max(x—ε, 0) is finitely separated from the identity: take the integer multiples of ε not exceeding 1 as separating set M, and maybe draw a picture to see what happens.
When ε varies, those functions x ↦ max(x—ε, 0) form a chain whose supremum is the identity map. Hence [0, 1] is an FS-domain. It is much more of course. For example, it is a continuous complete lattice, and all continuous complete lattices are bc-domains, all bc-domains are RB-domains, and all RB-domains are FS-domains.
The FS-domain of closed discs in the plane
Here is the example mentioned by Achim Jung in [1]. Let Disc be the poset of all closed disc in R2, plus R2 itself, ordered by reverse inclusion. Hence R2 is the bottom element of Disc.
Achim mentions without proof that the filtered intersection of closed discs is a closed disc, and that is sufficiently obvious, geometrically, that I will avoid giving a formal proof of it. Hence Disc is a dcpo, and directed suprema are filtered intersections.
Since every closed disc is compact and R2 is well-filtered (since sober, since Hausdorff), Disc is a continuous dcpo, where a disc D is way-below another disc D’ if and only if the interior of D contains D’. Hence the Scott topology on Disc coincides with the so-called upper Vietoris topology, whose basic open subsets are ☐U = {D ∈ Disc | D ⊆ U}, U open in R2.
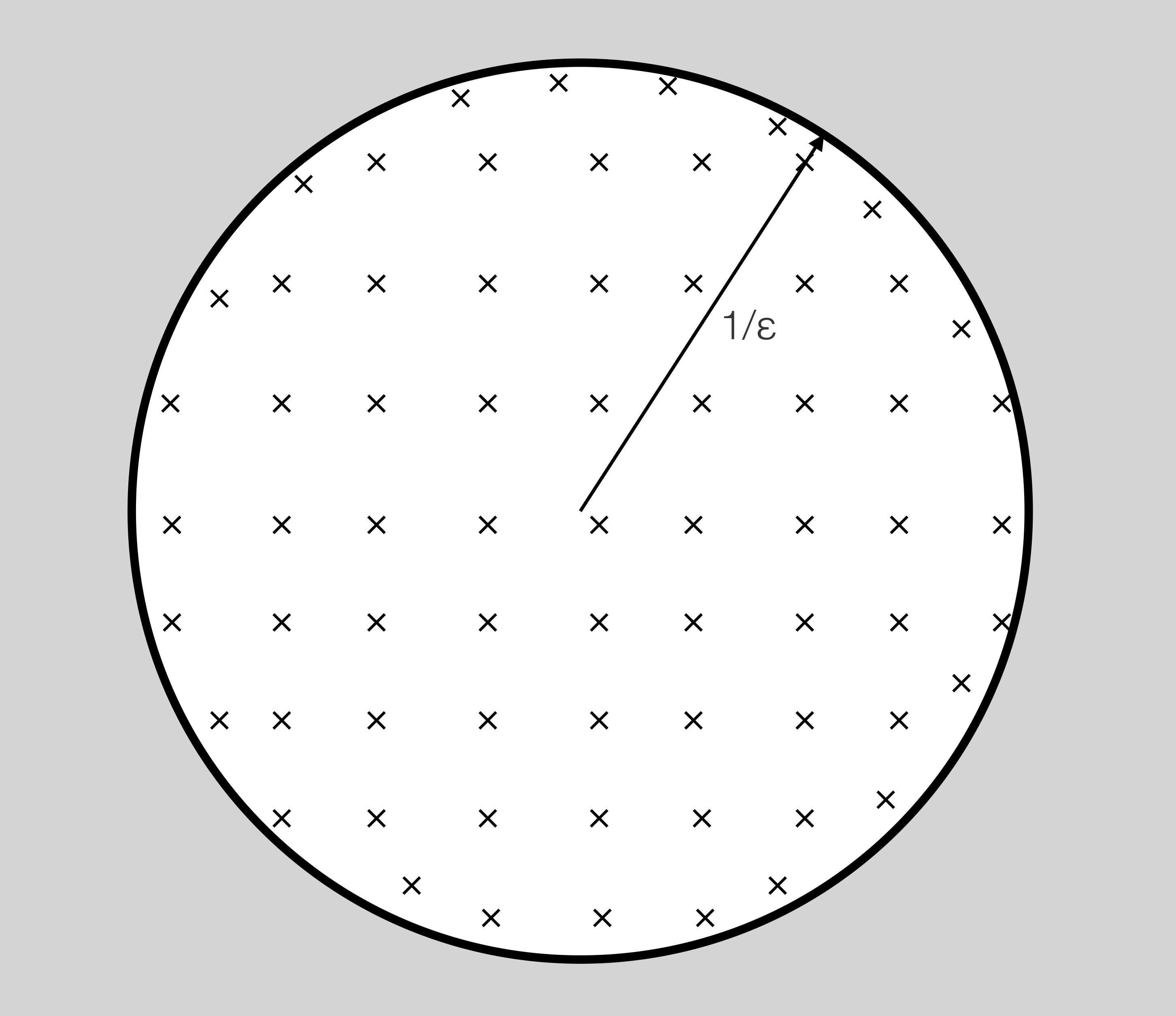
For every ε>0, Achim defines a map fε : Disc → Disc as follows: fε maps every closed disc D inside the open ball B(0,<1/ε) with center 0 and radius 1/ε to its ε-neighborhood, that is, to the disc with the same center and with radius equal to the radius of D, plus ε. All other discs, and the whole plane itself, are mapped to the bottom element R2.
This is really in the spirit of the function x ↦ max(x—ε, 0) we took to show that [0, 1] is an FS-domain.
Achim claims that fε is Scott-continuous. It is easier to prove that it is continuous with respect to the upper Vietoris topology, and to show that fε-1 (☐U) is open for every open subset U of R2. That is clear if U is the whole of R2, so let us assume it is not. Then fε-1 (☐U) is the set of closed discs D that are included in B(0,<1/ε) and in the “shrinking of U by ε”, U-ε, defined as the union of the open balls B(x, <r) such that the expanded ball B(x, <r+ε) is included in U. (I hope this is correct. I have not checked the details.)
The fact that fε is finitely separated from the identity seems less elementary to me. Achim has a very short argument, which however appeals to a lot of untold facts: that the upper Vietoris topology is one half of the so-called Vietoris topology, that the latter, once restricted to a compact subset of R2 (namely, the closed ball of center 0 and radius 1/ε), is metrized by the so-called Hausdorff metric, etc.
Lawson’s argument
Lawson [2] has a more elementary argument, and builds the separating set M explicitly. He actually proves a more general theorem, but here is what his construction gives us in the present case. As I have just said, the closed ball with center 0 and radius 1/ε is compact, hence it can be covered by finitely may open balls B(xi, <ε/3), 1≤i≤k.
Here is a picture of the situation. The small crosses are meant to be the set of points xi.
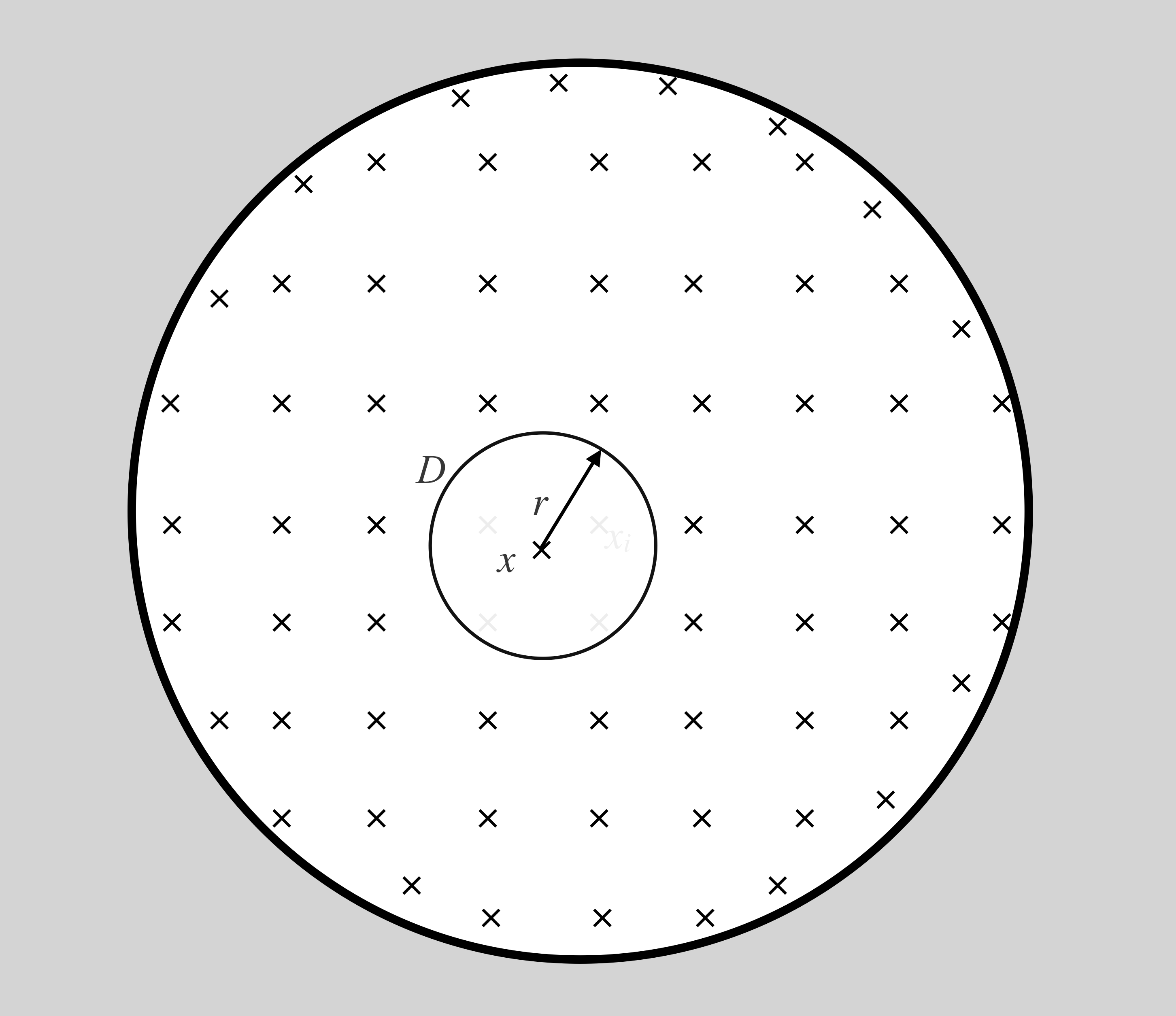
Let M be the set of closed discs with centers xi and radii εk/3, 2≤k≤3/ε2+1, plus the bottom element R2. For every disc D, if D is not included in B(0, <1/ε), then, choosing m=R2, we obtain fε(D) ≤ m ≤ D: good (remember that ≤ is reverse inclusion). Hence assume D⊆B(0, <1/ε).
Otherwise, let x be the center of D and r be its radius. Here is a picture of D:
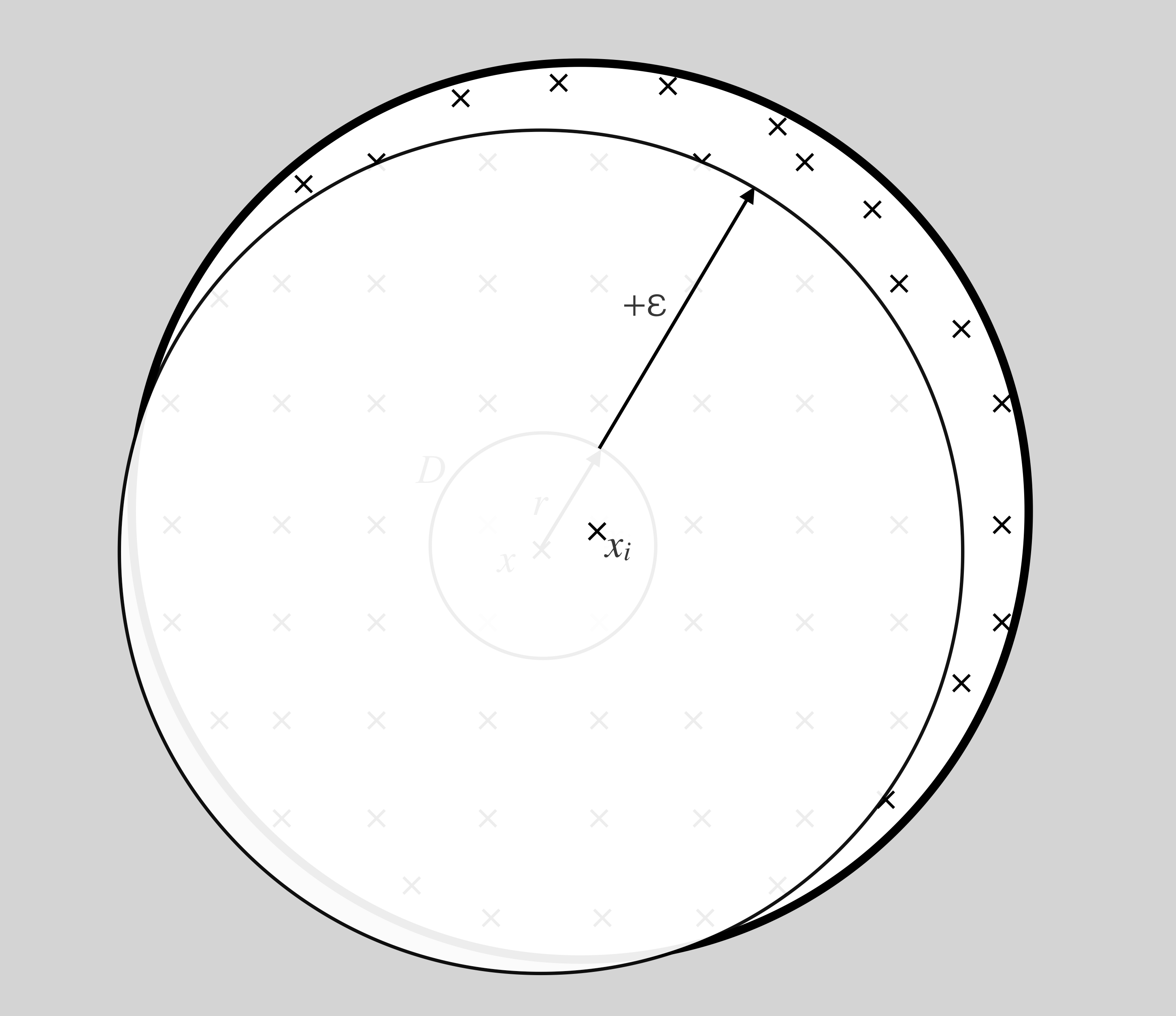
We recall that, in that case, fε(D) is the closed ball with center x and radius r+ε. This is a smaller element of Disc, but since the order is reverse inclusion, this is really a larger ball, geometrically:
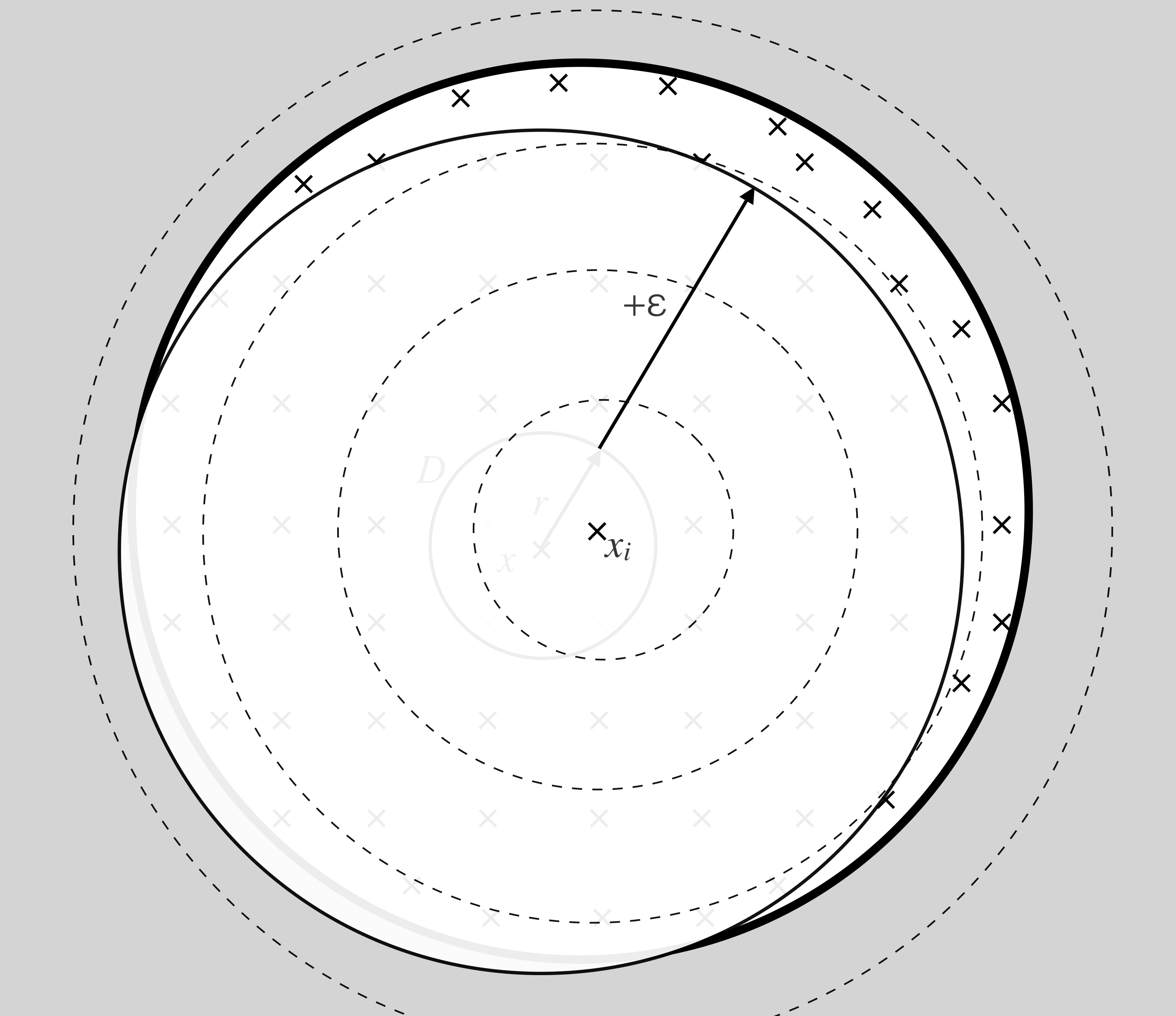
By construction, x is in some open ball B(xi, <ε/3). We have shown such an xi in the above picture. Let us look at the closed discs centered at xi, and whose radii are multiples of ε/3, so that they fall in M. Those are the discs shown with dashed lines below:
As the picture shows, one those dashed discs contains D and is contained in fε(D). Let us show that formally.
Since D⊆B(0, <1/ε), d(0,x)+r < 1/ε, where d(0,x) is the distance from 0 to x. That implies r < 1/ε. Let k≥2 be such that ε(k-2)/3≤r<ε(k-1)/3. We check easily that k≤3/ε2+1. We let m ∈ M be the closed disc with center xi and radius εk/3. Then:
- fε (D) is the closed disc centered at x with radius r+ε. Since that radius is ≥ε(k+1)/3, fε (D) contains m, namely fε(D) ≤ m. Indeed, every point z of m is such that d(xi, z) ≤ εk/3, so d(x, z) ≤ d(x, xi) + εk/3. Here we use the fact that d is a metric, whence d(x, xi) = d(xi , x) < ε/3. Therefore d(x, z) < ε(k+1)/3 ≤ r+ε.
- m itself contains D, namely m ≤ D. Indeed, every point z of D is such that d(x, z)≤r<ε(k-1)/3, so d(xi, z) < d(xi, x) + ε(k-1)/3 < εk/3.
The FS-domain of formal balls of certain quasi-metric spaces
Note how little we have used of the structure of closed discs of R2.
- We have used a compactness argument: closed discs are compact, hence can be covered by finitely many open balls of a specified radius—so we only need that closed discs are precompact, not compact.
- We have used the fact that d is a metric (not just a quasi-metric) in the argument that shows that fε(D) ≤ m.
- We have used the fact that the metric d is finite, namely d(x,y)<∞ for all points x, y. That is less visible, but is required to show that the family of maps fε has the identity as pointwise supremum: for that we need to show that every point x is at distance <1/ε of 0, namely d(0,x)<1/ε, for ε large enough.
- We have used the special point 0. Looking at the proof, we see that there is nothing special with it: we could have picked any other point.
- The final, and most important, point is that everything could have been done with formal balls instead of closed discs. Completeness is then required so that the poset of formal balls is a dcpo.
Doing the corresponding generalizations, we obtain what Lawson actually proved:
Let X,d be a complete metric space, with finite metric, in which closed discs are precompact. Then the dcpo B(X,d)⊥ of formal balls of X,d, with a fresh bottom element ⊥ adjoined, is an FS-domain.
Lawson also requires X, d to be separable, but I do not see where that would be required. (But it is an easy exercise to show that every metric space whose metric is finite and in which closed discs are precompact is separable.) Also, he does not explicitly require the metric to be finite, but that is because the standard definition of metrics in the literature includes finiteness.
This is really a generalization of the argument mentioned by Achim Jung in [1], because B(X,d)⊥ and Disc are order-isomorphic when X,d is the Euclidean plane; or any Rn.
It is not difficult to see that:
- We do not need d to be finite. There should merely exist a point, call it 0 again, such that every point x is at finite distance from 0, namely d(0,x)<∞ for every x in X.
- We do not need d to be a metric after all. If we take a quasi-metric instead, we should require the closed discs with center 0 to be totally bounded instead of precompact (i.e., covered by finitely many symmetrized balls of any given radius).
- Completeness is still required for B(X,d)⊥ to be a dcpo, and in that case, that should be understood as Yoneda-completeness, using the Kostanek-Waszkiewicz theorem (Theorem 7.4.27 in the book).
- Less visible is the fact that fε is no longer automatically Scott-continuous under those relaxations. For fε to be Scott-continuous, we need the set of formal balls mapped to ⊥ to be Scott-closed. We typically require X, d to be continuous, and we let fε map every formal ball (x, r) that is not in the Scott-open subset ↟(0, 1/ε) to ⊥. All others are mapped to (x, r+ε), and that is Scott-continuous because, in a Yoneda-complete quasi-metric space, directed suprema of formal balls are computed by taking d-limits of centers and infima of radii. (I’ll let you check that the supremum of those maps is the identity map. As a hint, since X, d to be continuous, for every formal ball (x, r), one can find (y, s) ≪ (x, r), and then (0, 1/ε) ≤ (y, s) for small enough ε>0 since d is finite.)
Then we obtain the following easy extension of Lawson’s result:
Let X,d be a continuous Yoneda-complete quasi-metric space. Assume there is a point 0 such that d(0,x)<∞ for every x in X, and that the closed balls centered at 0 are totally bounded. Then the dcpo B(X,d)⊥ of formal balls of X,d, with a fresh bottom element ⊥ adjoined, is an FS-domain.
I find that result interesting because it in particular implies that a continuous Yoneda-complete quasi-metric space with the properties given above has a coherent dcpo of formal balls. This is a consequence of the fact that every FS-domain is coherent (since stably compact, see Exercise 9.6.26 in the book). Using the d-Scott topology, the compact saturated subsets of X are then the compact saturated subsets of B(X,d)⊥ that are included in X, and that shows:
Corollary. Let X,d be a continuous Yoneda-complete quasi-metric space. Assume there is a point 0 such that d(0,x)<∞ for every x in X, and that the closed balls centered at 0 are totally bounded. Then X is coherent in its d-Scott topology.
(For metric spaces, instead of quasi-metric spaces, that would hold vacuously, since metric spaces are T2 hence coherent in any case.)
Returning to RB-domains, one path towards separating RB-domains from FS-domains would be to exhibit a Yoneda-complete quasi-metric space satisfying the above conditions and such that B(X,d)⊥ would not be an RB-domain. I am not claiming that the result I have just mentioned will help us, though: the difficulty lies in showing that a given FS-domain is not an RB-domain.
— Jean Goubault-Larrecq (April 29th, 2018)![]()
- Achim Jung. The classification of continuous domains. Proceedings of the 5th Annual IEEE Symposium on Logics in Computer Science (LICS’90), 1990, pages 35-40.
- Jimmie Lawson. Metric spaces and FS-domains. Theoretical Computer Science 405(1-2), 2008, pages 73-74.